广义D3模

王永铎，秦丽芳

(兰州理工大学 理学院,甘肃 兰州 730050)

文中记R是有单位元的结合环，M是右R模，N≤M表示N是M的子模，N|M表示N是M的直和项，r(A)表示A在R中的右零化子，E(M)表示M的内射包，EndR(M)表示M的自同态环，HomR(X,Y)表示R-模X到Y的同态集.

2014年，Amin等[1]引入了D3模.称M是D3模，如果M1|M,M2|M且M=M1+M2，那么M1∩M2是M的直和项.文献[1]证明了所有R-模是D3模当且仅当R是半单环，当且仅当所有内射R-模的商模是D3模，当且仅当任意两个D3模的直和是D3模，当且仅当R-模(R⊕R)R的商模是D3模.2019年，Tademir等[2]引入了广义SIP模(简称GSIP模).称M是GSIP模，如果M的任意两个直和项的交同构于M的直和项.受文献[1，2]的启发，我们引入了广义D3模(简称G-D3模)的概念.称M是G-D3模，如果M1|M,M2|M且M=M1+M2，那么M1∩M2同构于M的直和项.文中给出了G-D3模和D3模互不包含的例子，证明了：遗传环R是半单环当且仅当所有R-模是G-D3模，当且仅当所有内射R-模的商模是G-D3模；遗传环R是右V-环当且仅当每个有限余生成R-模是G-D3模，当且仅当每个有限余表示R-模是G-D3模.称M是SSP模[3]，如果M的任意两个直和项的和是M的直和项.称M是virtually半单模[4]，如果M的每个子模同构于M的直和项.称M的子模N是完全不变子模[5]，如果对任意的f∈EndR(M),均有f(N)⊆N.称M是(弱)duo模[5]，如果M的每个(直和项)子模是完全不变子模.称M是有限余生成模[6]，如果M的基座是有限生成的且在M中本质.称X是有限余表示模[6]，如果X是有限余生成的，且正合列0→X→L→N→0中L是有限余生成的，N也是有限余生成的.称M满足C2条件[7]，如果同构于M的直和项的子模N是M的直和项.称R是右V-环[6]，如果任意单右R-模是内射模.

1 主要结果

定义1称M是广义D3模(简称G-D3模)，如果M1|M,M2|M且M=M1+M2，那么M1∩M2同构于M的直和项.

证明由文献[4]例2.7可知:MR是virtually半单模，所以MR是G-D3模.因为D3模的直和项仍为D3模，而Z4⊕Z2不是D3模，所以MR不是D3模. 】

定理1设M是G-D3模.若M=A⊕B，其中A,B≤M,f:A→B是满同态，则Kerf同构于M的直和项.

证明设T={a+f(a)|a∈A},则T≤M.设x∈M,x=a+b,a∈A,b∈B，则x=a+f(a)-f(a)+b∈T+B,因此M=T+B.再设x=a+f(a)∈T∩B，其中a∈A，则a=x-f(a)∈A∩B=0，从而a=0，故x=f(a)=0,因此T∩B=0.这样M=T⊕B.

设x∈M=A⊕B，则x=a+b，其中a∈A,b∈B.因为f是满同态，所以存在a1∈A，使得b=f(a1)，从而x=a+b=a+f(a1)=a-a1+a1+f(a1)∈A+T，即M=A+T．又因为M是G-D3模，所以A∩T同构于M的直和项．

设x∈A∩T，则x=a=a1+f(a1)，其中a,a1∈A，从而a-a1=f(a1)∈A∩B=0，进而x=a=a1,f(x)=f(a)=f(a1)=0，因此x∈Kerf,即A∩T⊆Kerf．设x∈Kerf，则x=x+f(x)∈A∩T，从而Kerf⊆A∩T．因此Kerf=A∩T．又因为A∩T同构于M的直和项，所以Kerf同构于M的直和项． 】

推论1设M是G-D3模．若M=A+B，其中A|M,B≤M,M/A≅M/B，则A∩B同构于M的直和项．

证明因为A|M，所以存在N≤M，使得M=A⊕N，从而N≅M/A≅M/B=(A+B)/B≅A/(A∩B)．这样，存在满同态f:A→N使得Kerf=A∩B，故由定理1知，Kerf同构于M的直和项，即A∩B同构于M的直和项． 】

命题1设M是R-模,则M是G-D3模当且仅当对于M=K⊕K′=L⊕L′=K+L且π:M→K′是标准投影，Ker(π|L)同构于M的直和项．

证明必要性.设M是G-D3模．因为M=K⊕K′,π:M→K′是标准投影，所以Kerπ=K，从而Ker(π|L)=Kerπ∩L=K∩L．又因为M是G-D3模且M=K+L，所以K∩L同构于M的直和项，即Ker(π|L)同构于M的直和项．

充分性.设K|M，L|M且M=K+L．因为K|M，所以存在K′≤M，使得M=K⊕K′．设π:M→K′是标准投影，则Ker(π|L)=K∩L．由假设知，Ker(π|L)同构于M的直和项，从而K∩L同构于M的直和项，即M是G-D3模． 】

定理2设M是G-D3模,则M是D3模当且仅当对于A1|M,A2|M,M=A1+A2且有R-同构σ:A1∩A2→P，其中P|M，σ可以扩张成某个θ∈EndR(M)．

证明必要性.设A1|M,A2|M,M=A1+A2且有R-同构σ:A1∩A2→P，其中P|M．因为M是D3模，所以(A1∩A2)|M，从而存在B≤M，使得M=(A1∩A2)⊕B．通过θ(a+b)=σ(a)定义θ:M→M，其中a∈A1∩A2,b∈B．因此对任意的a∈A1∩A2,有θ(a)=σ(a)，故θ|A1∩A2=σ．

充分性.设A1|M,A2|M,M=A1+A2．因为M是G-D3模，所以存在P|M，使得σ:A1∩A2→P是同构且σ(A1∩A2)|M，从而由假设知，σ可以扩张成同态θ:M→M．设π:M→σ(A1∩A2)是标准投影，则ψ=πθ:M→σ(A1∩A2)是同态．因此对任意的x∈A1∩A2,ψ(x)=πθ(x)=πσ(x)=σ(x)．因为对任意m∈M,ψ(m)=σ(n)=ψ(n),n∈A1∩A2，所以m-n∈Kerψ．而m=m-n+n，故M=Kerψ+(A1∩A2)．设z∈Kerψ∩(A1∩A2)，则z∈A1∩A2,z∈Kerψ，从而ψ(z)=0,σ(z)=ψ(z)=0,因此z=0．这样M=Kerψ⊕(A1∩A2)，进而(A1∩A2)|M，即M是D3模． 】

命题2若R-模M满足C2条件，则M是G-D3模当且仅当M是D3模．

证明必要性.设A1|M,A2|M,M=A1+A2．因为M是G-D3模，所以存在K|M，使得(A1∩A2)≅K．又因为M满足C2条件，所以(A1∩A2)|M，即M是D3模．

充分性.显然． 】

推论2内射模M是G-D3模当且仅当M是D3模．

下面的例3说明两个G-D3模的直和不一定是G-D3模．

例3考虑Z-模Z8⊕Z2．因为Z8,Z2是不可分解模，所以Z8,Z2是G-D3模．通过

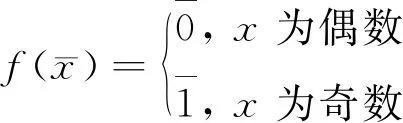
引理1[8]设R-模M=M1⊕M2．若r(M1)+r(M2)=R，则对于任意的N≤M有N=N1⊕N2，其中N1≤M1,N2≤M2．

定理3设P是R-模．若P=A⊕B是P的一个分解，A,B是G-D3模,且r(A)+r(B)=R，则P是G-D3模．

证明设X|(A⊕B),Y|(A⊕B),A⊕B=X+Y.由引理1知，X=A1⊕B1,Y=A2⊕B2，其中A1≤A,A2≤A,B1≤B,B2≤B，因此A1|A,A2|A,B1|B,B2|B．因为A⊕B=X+Y，所以A+B=X+Y=A1+B1+A2+B2=A1+A2+B1+B2，从而A=A1+A2,B=B1+B2．又因为A,B是G-D3模，所以A1∩A2同构于A的直和项，B1∩B2同构于B的直和项，从而(A1∩A2)⊕(B1∩B2)同构于A⊕B的直和项．

下证(A1∩A2)+(B1∩B2)=(A1+B1)∩(A2+B2)．设a+b∈(A1∩A2)+(B1∩B2)，其中a∈A1∩A2,b∈B1∩B2，则a∈A1且a∈A2,b∈B1且b∈B2，从而a+b∈A1+B1且a+b∈A2+B2．因此a+b∈(A1+B1)∩(A2+B2)，即(A1∩A2)+(B1∩B2)⊆(A1+B1)∩(A2+B2)．设x=a1+b1=a2+b2∈(A1+B1)∩(A2+B2)，其中a1∈A1,b1∈B1且a2∈A2,b2∈B2，则a1-a2=-b1+b2∈(A1+A2)∩(B1+B2)=0，从而a1=a2∈A1∩A2,b1=b2∈B1∩B2．因此x=a1+b1=a2+b2∈(A1∩A2)+(B1∩B2)，即(A1+B1)∩(A2+B2)⊆(A1∩A2)+(B2∩B2)．故(A1∩A2)+(B1∩B2)=(A1+B1)∩(A2+B2)，进而(A1∩A2)⊕(B1∩B2)=(A1⊕B1)∩(A2⊕B2)=X∩Y.因此X∩Y同构于A⊕B的直和项，即P=A⊕B是G-D3模． 】

定理4设M是G-D3模．若M=M1⊕M2是M的一个分解且有Hom(M1,M2)=0，则M2是G-D3模．

证明设A|M2,B|M2且M2=A+B，则A|M,B|M．因为M=M1⊕M2，所以M=M1⊕(A+B)．又因为M是G-D3模，(M1⊕A)|M,B|M，所以存在N|M，使得(M1⊕A)∩B≅N．而(M1⊕A)∩B=A∩B，因此A∩B≅N．因为N|M，所以存在N′≤M，使得M=N⊕N′．又因为Hom(M1,M2)=0，所以由文献[5]引理1.9知，M1是M的完全不变子模，从而M1=M∩M1=(N⊕N′)∩M1=(N∩M1)⊕(N′∩M1)．因为Hom(M1,N)=0(若Hom(M1,N)≠0，则有非零同态f:M1→N≅A∩B→M2与Hom(M1,M2)=0矛盾)，所以N∩M1=0(若有非零元x∈N∩M1，则M1→N∩M1→N非零与Hom(M1,N)=0矛盾)，从而M1≤N′．因此N′=M1⊕(N′∩M2)．又因为M=N⊕N′，所以M=N⊕M1⊕(N′∩M2)=M1⊕M2，从而M2≅N⊕(N′∩M2)，进而N同构于M2的直和项．因此A∩B同构于M2的直和项，即M2是G-D3模． 】

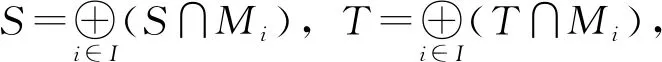
命题3设M是G-D3模．若M是SSP模，则M是GSIP模．

证明设X|M,Y|M．因为M是SSP模，所以(X+Y)|M，故存在L≤M，使得M=(X+Y)⊕L．因为X,Y,L是M的直和项且M是SSP模，所以(X+L)|M,(Y+L)|M．又因为M=(X+L)+(Y+L)且M是G-D3模，所以(X+L)∩(Y+L)同构于M的直和项．显然(X+L)∩(Y+L)=[X∩(X+Y)]+L．设x=x1+x2∈X∩(Y+L)，其中x∈X,x1∈Y,x2∈L，则x2=x-x1∈(X+Y)∩L=0，从而x-x1=x2=0．因此x=x1∈X∩Y，即X∩(Y+L)⊆X∩Y．显然X∩Y⊆X∩(Y+L),所以X∩Y=X∩(Y+L),(X∩Y)+L=[X∩(Y+L)]+L．于是有(X+L)∩(Y+L)=[X∩(Y+L)]+L=(X∩Y)⊕L．

记P=(X+L)∩(Y+L)=(X∩Y)⊕L，则(X∩Y)|P．又因为P同构于M的直和项，所以存在K|M，使得P≅K，从而X∩Y同构于K的直和项，进而X∩Y同构于M的直和项，即M是GSIP模． 】

推论4设M是SSP模，则M是G-D3模当且仅当M是GSIP模．

命题4设R是交换的Noetherian环，M=M1⊕M2，其中M1,M2是M的不可分解子模．若M是G-D3模且满足C2条件，f:M1→M2是满同态，则f=0或f是同构，且对于每一个非零的x∈M1,r(x)=A，其中A是R的素理想．

证明设f≠0．因为M是G-D3模且满足C2条件，所以由命题2知，M是D3模，从而由文献[1]命题4知，Kerf|M1．又因为M1是不可分解子模且f≠0，所以Kerf=0，从而f是单同态，即f是同构．

设0≠x,y∈M1且a∈r(x),a∉r(y)(即r(x)≠r(y))．通过β(m)=f(ma)定义β:M1→M2，其中m∈M1，则显然β是满同态．因为a∈r(x)，所以xa=0，从而f(xa)=β(x)=0．因此x∈Kerβ．又因为x≠0，所以β不是单同态，且不是同构．因为a∉r(y)，所以ya≠0，从而f(ya)=β(y)≠0．因此β≠0，即β不是零同态．又因为M=M1⊕M2是D3模，所以Kerβ|M1，从而Kerβ=0与β不是单同态矛盾．因此对于所有非零的x,y∈M1,有r(x)=r(y)．故由文献[9]定理6知，r(x)是素理想. 】

定理5设R是遗传环,则下列条件等价：

(1)R是半单环；

(2)所有R-模是G-D3模；

(3)所有内射R-模的商模是G-D3模．

证明(1)⇒(2)⇒(3)显然．

(3)⇒(1).因为R是遗传环，所以由文献[10]练习18.10知，内射R-模的商模仍是内射模，从而由推论2知，所有内射R-模的商模是D3模．由文献[1]命题30知，R是半单环． 】

命题5设R是遗传环,则下列条件等价：

(1)R是Noetherian环，且G-D3模的直和仍为G-D3模；

(2)R是半单环．

证明(1)⇒(2).设M是内射R-模的商模．因为R是遗传环，所以由文献[10]练习18.10知，内射R-模的商模仍是内射模，从而M是内射R-模．又因为R是Noetherian环，所以由文献[11]定理6.6.4知，M是不可分解子模的直和．而不可分解模是G-D3模，所以M是G-D3模，再由定理5知，R是半单环．

(2)⇒(1).若R是半单的，则由文献[6]知，所有R-模是内射模;再由定理5可知，所有R-模是G-D3模，从而内射R-模的直和仍为内射模．因此由文献[10]命题18.13易知，环R是Noetherian环，且G-D3模的直和仍为G-D3模． 】

引理2[6]设R是环,则下列条件等价：

(1)R是右V-环；

(2)每个有限余生成R-模是半单模；

(3)每个有限余表示R-模是内射模．

定理6设R是遗传环,则下列条件等价：

(1)R是右V-环；

(2)每个有限余生成R-模是G-D3模；

(3)每个有限余表示R-模是G-D3模．

证明(1)⇒(2).由文献[6]可得．

(2)⇒(3).由定义可得．

(3)⇒(1).设M是有限余表示R-模．由文献[6]知，E(M)和E(M)/M是有限余生成的．因为R是遗传环，所以内射模的商模是内射模，从而E(M)/M是内射模．又因为有限余生成内射模是有限余表示的，所以由假设和文献[6]知，E(M)⊕E(M)/M是G-D3模．设f:E(M)→E(M)/M是满同态，则由定理1知，Kerf=M同构于E(M)⊕E(M)/M的直和项．因为内射模的直和项仍为内射模，所以M同构于内射模．因此由引理2知，R是右V-环． 】

命题6如果遗传环R满足“G-D3模的直和仍为G-D3模”，那么R是右V-环．

证明设M是有限余生成R-模，则由文献[6]知，M是不可分解模的直和．因为不可分解模是G-D3模，所以M是G-D3模的直和，进而由假设知，M是G-D3模．因此由定理6知，R是右V-环． 】