基于决策者确定型偏好的Pythagorean模糊集决策模型
陈孝国,黄鸿辉,杨悦,3,余高锋,王佑恩
ZADEH[1]提出的模糊理论是处理不确定性问题的有效工具,但仅用隶属度来描述信息略显不足,为了弥补这个缺陷,ATANASSOV[2]提出了直觉模糊集,用隶属度、非隶属度和犹豫度来表达不确定性信息,但仍然无法解决隶属度和非隶属度加和大于1的决策问题.2013年,美国学者YAGER[3]提出了Pythagorean模糊集,其由隶属度与非隶属度两部分组成,同时满足隶属度与非隶属度的平方和小于等于1,使它对隶属度和非隶属度的处理更加符合现实情况.目前已经有大量关于Pythagorean模糊集决策问题的研究,李娜等[4]将基于模糊测度的Choquet积分引入Pythagorean模糊集中,弥补了已有决策方法中假设属性间相互独立,而忽略属性相互关联性的不足.梁霞等[5]基于Pythagorean语言集,将TODIM方法、Choquet积分和Shapely函数结合提出了Pythagorean不确定语言集的TODIM方法及其应用,将属性相互关联下的决策方法引入Pythagorean语言集中.施明华等[6]提出了一种基于证据理论和加权MSM算子Pythagorean群决策方法,弥补了传统Bonferroni平均等算子在捕获变量间的关联性不够灵活的缺陷.陈孝国等[7]改进了现有支持度存在的缺陷,提出了一种新的加权支持度,并在Pythagorean模糊环境下建立了决策方法.刘政敏等[8]研究了Pythagorean不确定语言集的语言变量的运算法则、大小比较方法和距离测度等,然后提出扩展的VIKOR多属性群决策方法.杨悦等[9]给出了基于Pythagorean集的犹豫模糊灰色关联前景多属性决策方法,一定程度上提高了决策的灵活性,降低了决策信息的损耗.范建平等[10]将模糊交叉熵概念引入Pythagorean模糊集中提出了Pythagorean模糊环境下的TOPSIS的多准则决策方法.杜玉琴[11]定义了Pythagorean梯形模糊语言集,提出Pythagorean梯形模糊语言集的计算规则、得分函数、加权算术平均算子和大小比较方法,并给出了Pythagorean梯形模糊语言集结算子的应用.
基于上述研究可以看出,大多数研究都没有考虑决策者对方案的偏好因素,然而在现实生活中决策者会因为经验和学术背景的不同而对方案偏好程度有所不同,进而影响决策结果.对此本文给出一种决策者确定型偏好的Pythagorean模糊集决策模型.近一步丰富关于毕达哥拉斯模糊集的决策方法.本文针对决策者对备选方案有自己的主观偏好,且偏好信息和评价信息均为Pythagorean模糊数的多属性决策问题,从因素权重完全未知和部分未知的角度构建基于Pythagorean模糊交叉熵和灰色关联分析的综合决策模型,利用拉格朗日乘子法和优化理论求解权重,并通过改变灰色分辨系数的取值做扰动分析来检验决策结果的可靠性,为毕达哥拉斯模糊集在复杂决策领域上的建立提供理论支撑.
1 Pythagorean模糊集
定义1[12]设非空集合X中任意的Pythagorean模糊集为up(x)和vp(x)分别表示P中元素x∈X的隶属度和非隶属度,满足0≤(up(x))2+(vp(x) )2≤1,up(x)∈[0,1],vp(x)∈[0,1].πp(x)为 犹 豫度,的值越小说明关于x的信息越多,反之信息越少.
通常记P=(up,vp)为 一 个Pythagorean模糊数.
定 义2[12]P的 补 集 定 义 为PC,PC=
定 义3[12]分别为两个Pythagorean模糊数,若up1≥up2且vp1≤vp2,则称P1≥P2.
定义4[13]设P1=(up1,vp1)和P2=(up2,vp2)分别为两个Pythagorean模糊数,定义:

定 义5[12]Pythagorean模糊 数 集 间 的 距 离定义如下:

定 义6[10]设P1,P2为 两 个Pythagorean模糊集,P1=(uP1(xi),vP1(xi)),P2=(uP2(xi),vP2(xi)),则P1,P2之 间 的Pythagorean模 糊 交 叉 熵IPFS(P1,P2)可定义为:

式中IPFS(P1,P2)说明了P1,P2之间的差异程度,但由于IPFS(P1,P2)不具有对称性,所以P1,P2之 间的对 称Pythagorean模 糊 交叉 熵可定义为:

定 理1[10]设P1,P2为 两 个Pythagorean模糊集,将P1,P2之间的模糊交叉熵定义为DPFS*(P1,P2),则下列定理成立:
③DPFS*(P1,P2)≥0(其中DPFS*(P1,P2)=0当且仅当P1=P2);
④P1,P2之间区别越大,则DPFS*(P1,P2)越大.
2 基于Pythagorean模糊数的决策方法
2.1 决策者确定型偏好的决策
本文研究的决策者对方案偏好确定的多属性问题均假设决策者对各备选方案有确定的主观偏好,基于Pythagorean模糊数的这类决策问题的一般描述为:决策者从众多备选方案Ai(i=1,2,…,m)中,根据属性值Cj(j=1,2,…,n),给出Pythagorean模糊数(uij,vij)形式表示的属性值,其中,uij和vij分别表示决策者对于方案Ai在属性Cj条件下的赞同程度和反对程度,为犹豫程度,且满足为属性权重,且满足同时决策者对于方案Ai的主观偏好值οi=(uij,vij)(i=1,2,…,m)也以Pythagorean模糊数的形式给出,最后通过计算综合灰色关联度系数值来对方案进行排序.
2.2 决策步骤
①确定备选方案Ai(i=1,2,…,m)在属 性Cj(j=1,2,…,n)下的主观评价矩阵Rmn和决策者对方案Ai的主观偏好值οi=(uij,vij)(i=1,2,…,m).
②计算基于Pythagorean模糊交叉熵距离下的各方案主观评价值相对于决策者的主观偏好值的灰色关联度系数,具体公式如下:

③确定属性Cj的权重ωj.
④计算各备选方案Ai在所有属性下的综合灰色关联度系数,公式如下:

⑤通过γi数值大小来对方案进行排序,即γi越大方案排序越靠前,使ξ变化做扰动分析,检验决策方法的稳定性.
⑥确定最终排序.
2.3 属性权重的确定
①权重信息完全未知.为了解决在权重信息完全未知的情况下客观权重的确定方法,可以采用离差最大化的思想确定权重,即对于一个多属性决策问题,一个属性对于不同方案的偏差值越大,则属性所占的权重就越大,如果一个属性对于所有方案的赋值一样,则可以认为该属性的权重为0.
对于属性Cj,方案Ai对于其他所有方案的偏差为j=1,2,…,n.所有方案对于其他方案的偏差值为

1.1.1 稻耐旱性资料 以《中国稻作资源目录》[6]资料为基础,对云南省稻耐旱性信息进行收集整合,主要针对苗期耐旱信息,共收集整理2 440份云南地方稻种资源稻耐旱性的相关资料信息。
构造拉格朗日函数L(λ,ωj)=L(λ,ωj)中的λ,ωj求偏导如下:

求得权重如下:

进行归一化处理如下:
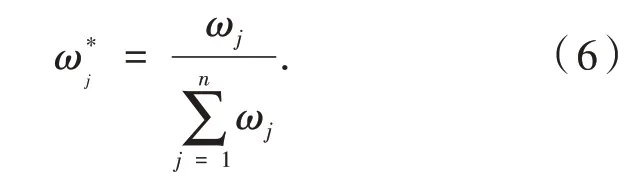
②权重信息部分未知.对于权重信息部分未知的情况,为了保证决策方法有效性,给出一种基于备选方案Ai的主观评价值相对于主观偏好值的相似程度最大化的客观权重确定方法.建立如下优化模型:

由此线性规划可解出属性Cj的权重ωj.其中ωj∈W包含下列五种情况:①ωk>ωt;②ωk-ωt≥c,其 中c>0;③ωk≥cωt,其 中c>0;④c≤ωi≤c+τ,其中c>0,τ>0;⑤ωk-ωt≥ωl-ωe,其中t≠l≠e.
3 实例分析
设某保险公司需要对研发部门提供的四款理财产品Ai(i=1,2,3,4)进行联评,初步选定4个属性指标Cj(j=1,2,3,4)来考查各个产品质量,C1为收益率,C2为系统性风险,C3为市场营销力度,C4为资金监管能力.由于人们对风险性和收益率的认识差别,使得该问题存在一定的主观偏好.经查阅数据资料,决策者对理财产品Ai在不同属性Cj下的评价值采同时对用Pythagorean模糊数表示,评价所得Pythagorean模糊决策矩阵R44如表1所示.

表1 Pythagorean模糊决策矩阵R44
决策者对产品Ai的主观偏好为:ο1=( 0.7,0.4),ο2=( 0.6,0.3),ο3=( 0.7,0.2),ο4=( 0.3,0.5).利用定义6计算各理财产品Ai的主观评价值相对于主观偏好值οi的Pythagorean模糊交叉熵距离,构成距离矩阵DPFS*.

根据式(1)计算各理财产品Ai的主观评价值与主观偏好值οi的灰色关联度系数,这里先令ξ=0.5,计算出系数矩阵γ.

然后计算各属性Cj的权重.
①若权重信息完全未知,则利用式(6)计算 权 重ω*=(0.259 8,0.229 4,0.190 2,0.320 6).利用式(2)计算出各产品的综合关联度系数γi.其中γ1=0.502 3,γ2=0.5710,γ3=0.725 4,γ4=0.606 8.根据γ3>γ4>γ2>γ1得到产 品排序结果为A3>A4>A2>A1.现在通过改变ξ的值做扰动分析来检验方案的可靠性,随机选 取ξ=0.2,ξ=0.36,ξ=0.6,ξ=0.86,ξ=0.93,得到各产品的综合关联度系数和排序结果,如表2所示.
从表2可以看出,在权重信息完全未知的情况下,当改变灰色分辨系数ξ的值,决策结果也没发生变化,说明该决策模型在权重信息完全未知的情况下具有一定的稳定性.

表2 权重完全未知前提下不同灰色分辨率对应的决策结果
②经咨询领域专家,初步确定权重范围为0.2≤ω1≤0.3,0.22≤ω2≤0.28,0.22≤ω3≤0.30,0.25≤ω4≤0.30.利用式(7)计算权重,构建灰色关联度系数最大化为目标的规划模型,形式如下:

利用MATLAB 7.0计算结果ω=(0.255 6,0.244 4,0.222 2,0.277 8).
根据式(2)计算出各产品的综合关联度系数γi.其中γ1=0.544 8,γ2=0.544 5,γ3=0.762 1,γ4=0.572 1.根据γ3>γ4>γ1>γ2可得产品排序结果为A3>A4>A1>A2,现在通过改变ξ的值做扰动分析来检验产品的可靠性,随机选取ξ=0.2,ξ=0.36,ξ=0.6,ξ=0.86,ξ=0.93得到各产品的综合关联度系数和排序结果,如表3所示.

表3 权重部分未知前提下不同灰色分辨率对应的决策结果
从表3可以看出,在权重信息部分未知的情况下,当改变灰色分辨系数ξ的值,决策结果也没发生变化,说明该决策模型在权重信息部分未知的情况下具有一定的稳定性.
实例分析中采用优化模型求解权重,在不同灰色分辨系数下权重及综合关联度系数均能达到全局最优,且结果唯一.
4 结语
本文针对决策者对方案有偏好的情况,给出了基于Pythagorean模糊集的综合关联度系数分析法,首先用Pythagorean模糊数给出各方案在各属性下的评价值和方案的主观偏好值,再引入灰色关联度分析法对方案进行排序,得到本文的排序结果A3>A4>A1>A2,并通过控制灰色辨别系数的值对排序结果进行扰动分析,由分析结果可以看出,其决策结果有很高的稳定性.同时本文也有缺点,本文考虑的只是个体决策,而没有将其推广到群决策上.在现实世界中由于个体能力有限,所以很难通过个体决策得到比较完美的决策方案,而群决策就能很好地弥补这个缺陷,所以将综合关联度系数分析法推广到群决策上将是本文的改进方向.在下一步研究中还可以进一步考虑群决策中各专家所提供的方案偏好程度,以求得到一个所有专家都认可的方案.

