食饵具有Allee效应和双参数扰动的随机捕食-食饵种群的灭绝性研究

尹文倩

捕食-食饵关系是种群之间相互作用的基本关系之一，经典的捕食-食饵种群模型是由LOTKA［1］和VOLTERRA［2］提 出 的Lotka-Volterra模型［3］.很多动力学文献中对捕食-食饵种群模型都有广泛的研究.

在文献［4］中，作者研究了食饵具有Allee效应的确定性捕食-食饵种群模型.在实际生活中，种群会受到各种随机因素的影响，在文献［5］中，作者将文献［4］的模型中死亡率为d1的食饵种群和死亡率为d2的捕食者种群带有白噪声，从而得到随机捕食-食饵种群模型.

事实上，不仅死亡率会受到随机因素的影响，种群内部竞争强度也会受到随机因素的影响.基于文献［5］中的模型，本文除了将死亡率为d1的食饵种群和死亡率为d2的捕食者种群带有白噪声，将食饵种群的内部竞争强度也考虑在内，从而得到食饵具有Allee效应和双参数扰动的随机捕食-食饵种群模型.

1 正解的存在唯一性

本文考虑带有白噪声且种群内部竞争强度为α的食饵种群模型，从而得到如下食饵具有Allee效应和双参数扰动的随机捕食-食饵种群模型：

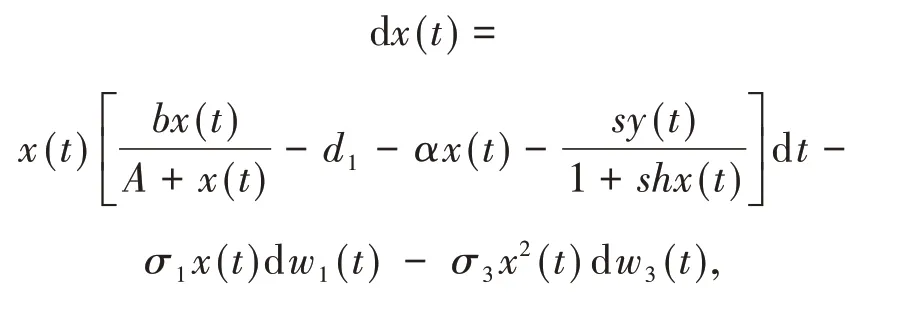
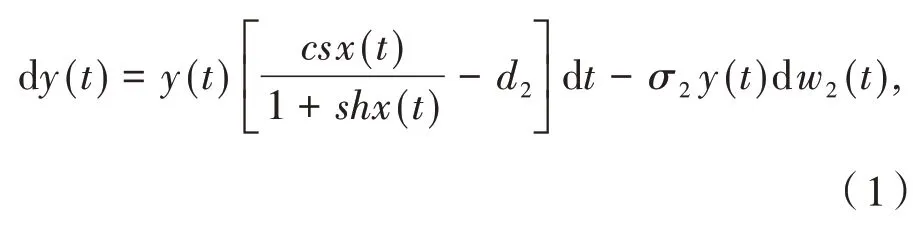
其 中：初 值x(0)=x0，y(0)=y0.这 里w={w1(t),w2(t),w3(t),t≥0}表示定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的三维标准布朗运动，分 别 表 示 噪 声w1(t)，w2(t)和w3(t)的强度.

模型中所有参数都假定为正数，它们的生物意义如下：b表示食饵种群的人均最大出生率，di(i=1,2)分别表示食饵种群和捕食者种群的平均最大死亡率，α表示食饵种群的种内竞争强度，s表示有效搜索率，h表示捕食者的处理时间，c表示摄取食饵转化成捕食者的换能效率，A表示食饵种群的Allee效应常数，sx(t)( 1+shx(t))表示捕食功能反应，即食饵密度与捕食者平均摄食量之间的关系.

模型（1）中x(t)和y(t)分别表示食饵和捕食者种群数量的大小，因此，这一部分研究模型（1）正解的存在唯一性.由于模型（1）的系数不满足线性增长条件，经典的随机微分方程理论对其不适用，因此为了证明模型（1）正解的存在唯一性，首先考虑方程

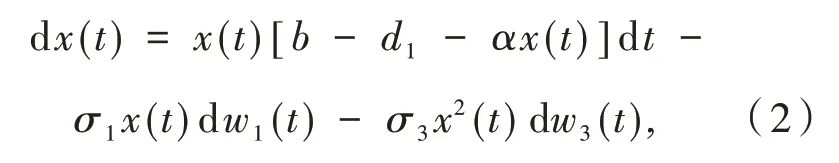
其中：初值x(0)=x0.

引理1对任意给定初值x0∈R+=(0,+∞)，对于任意t≥0，方程（2）存在唯一正解x(t)，即，以概率1有x(t)∈R+.

证明 对任意x0∈R+，首先考虑方程

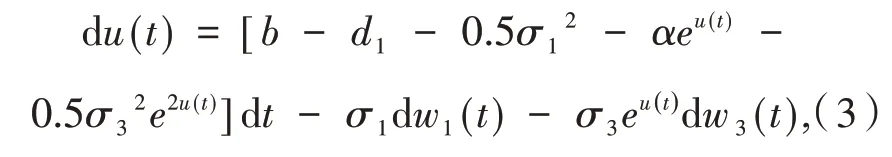
其中初值u(0)=logx0.显然，方程（3）的系数满足局部Lipschitz条件.因此，对给定初值u(0)，当t∈[0,τe)时方程存在唯一最大局部解u(t)，其中τe表示爆发时间.由̂公式可知，当t∈[0,τe)时，方程（2）存在唯一局部正解x(t)=eu(t).为了证明该解是全局的，只需证明τe=∞a.s.对x0∈( 1k0,k0)，令k0＞0且充分大，对任意整数k≥k0，定义停时

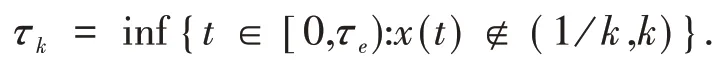
对 于 空 集∅，定 义inf∅=∞.显 然，当k→∞时，τk单调递增，同时对于τk∈[0,τe]极限存在.因此，定义显然τ∞是一个停时且τ∞≤τea.s.如果可以证明τ∞=∞a.s.那么对任意t≥0，有τe=∞a.s.对u＞0，易 知为 了证明τ∞=∞a.s.首先定义C2函数V:R+→R+，

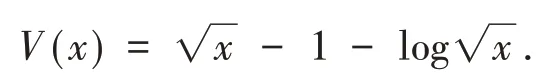
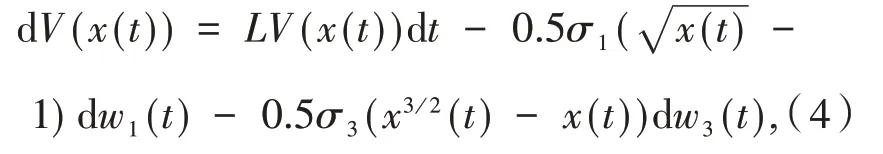
其中:LV:R+→R定义为

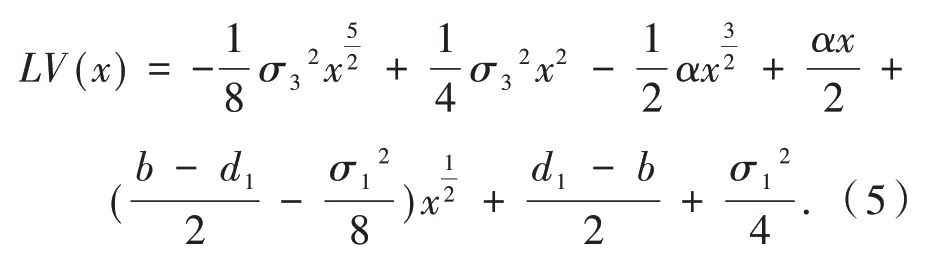
注意到LV(x)最高次系数为负，因此，存在K1＞0，使得

将上式代入式（5）得

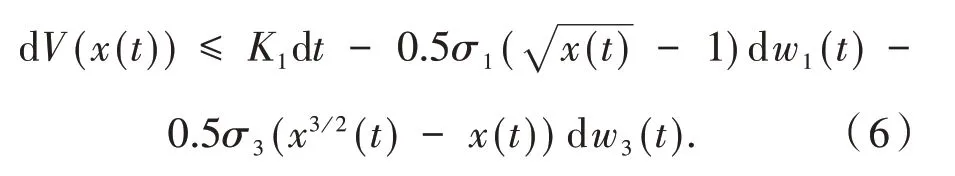
对任意k≥k0及T＞0，当t1∈[0,T]时，对上式两边分别从0到τk∧t1积分并取期望得

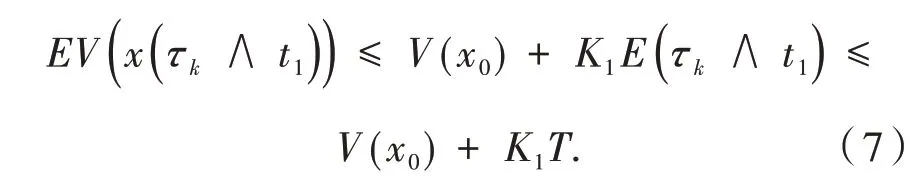
由此得

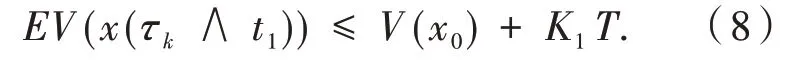
注意到，对任意ω∈{τk≤T},x(τk,ω)等于k或1k，因此

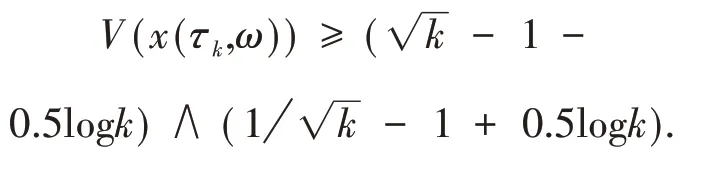
代入式（8）得

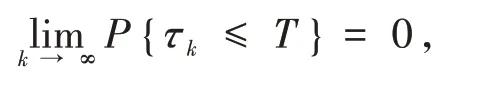
其中：I{τk≤T}表示集合{τk≤ T}的示性函数.

令k→∞，得

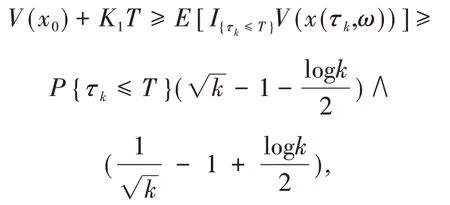
则P{τ∞≤T}=0.又因为T＞0是任意的，故P{τ∞＜∞}=0.因此P{τ∞=∞}=1.

定理1 对任意给定初值(x0,y0)∈={(x,y)∈R2:x＞0,y＞0}，当t≥0时，式（1）存在唯一正解，且存在ϕ(t),φ(t),ψ(t)和ξ(t)，使得对任意的t≥0，

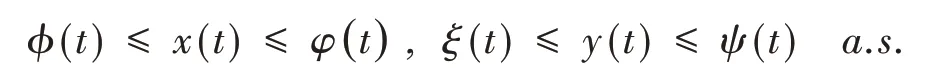
证明 对初值(x0,y0)∈，首先考虑模型

其中：初值(u(0),v(0))=(logx0,logy0).显然，该模型的系数满足局部Lipschitz条件，对于给定初值(u(0),v(0))，当t∈[0,τe)时，该模型存在唯一最大局部解(u(t),v(t))，其中τe为爆发时间.因此，利用公式可得，当t∈[0,τe)时，(x(t),y(t))=(eu(t),ev(t))是初值为(x0,y0)的模型（1）的唯一局部正解.

接着运用随机比较原理证明该解是全局的，即τe=∞.注意到，局部解(x(t),y(t))为正解.对于捕食者种群，有

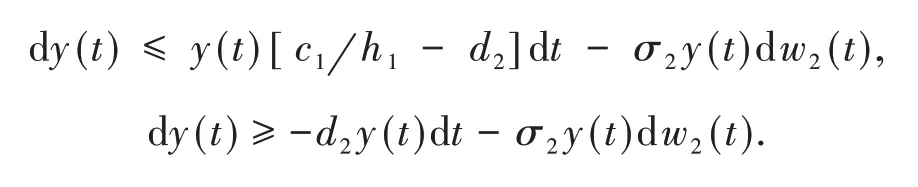
设ψ(t)是下列方程的唯一解

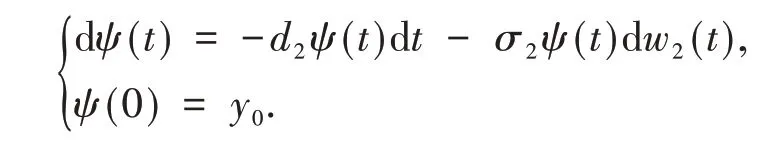
解得

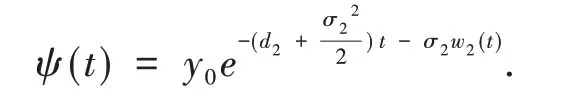
设ξ(t)是下列方程的唯一解

解得

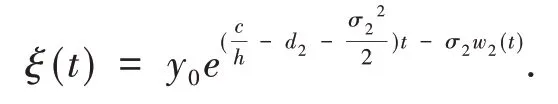
根据随机比较原理得，对任意的t∈[0,τe)，有

同理，对于食饵种群有

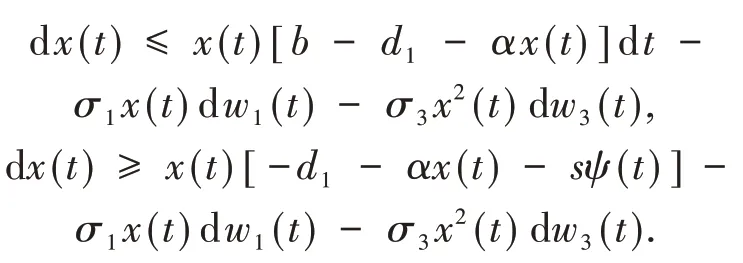
设ϕ(t)是下列方程的唯一解

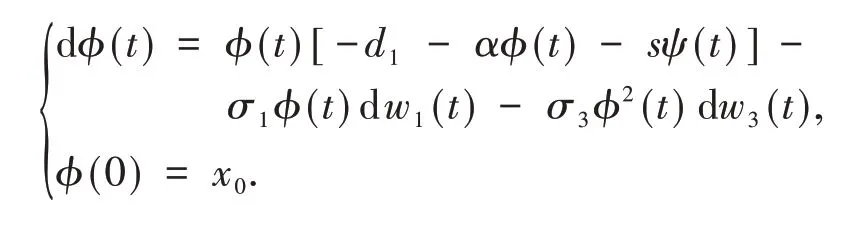
设φ(t)是下列方程的唯一解

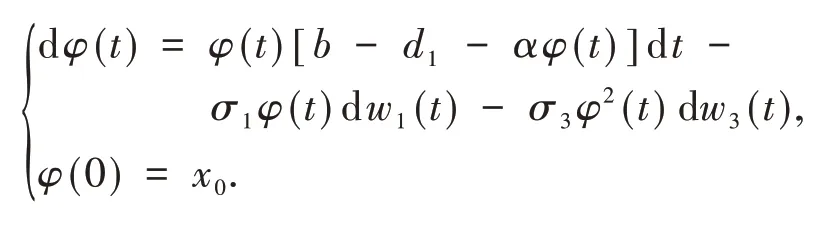
根据随机比较原理，对任意的t∈[0,τe)，有

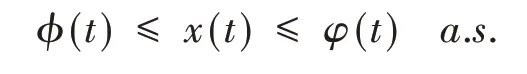
由引理1可知，对任意t≥0，存在唯一的φ(t),ϕ(t)，因此有τe=∞.

2 灭绝性

这一部分主要研究噪声强度及Allee效应如何影响食饵种群和捕食者种群灭绝的问题.首先给出种群灭绝的定义.

定义1若种群大小（或密度）x(t)满足

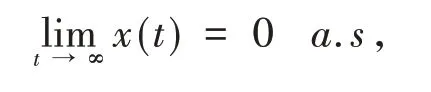
则称该种群以概率1灭绝.

下面的定理研究了噪声强度对捕食者种群的影响.

定理2设(x(t),y(t))是模型（1）的解，其初值(x0,y0)∈R+.若σ22＞2(c h-d2)，则

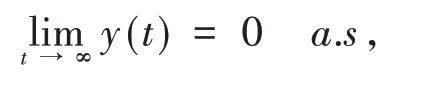
即捕食者种群以概率1呈指数灭绝.（证明过程见文献［5］的定理3.3）.

下面讨论Allee效应对食饵种群和捕食者种群的影响.

定理3设(x(t),y(t))是模型（1）的解，其初值(x0,y0)∈R+.若模型参数满足下列条件之一：

①d1＞b且αA≤0.5(d1-b)；

②d1≤b且αA≥b-d1, 或αA＜b-d1且

(b-d1-αA)2(b-d1+8αA)-27d1(αA)2＜0；

③αA≤b且则

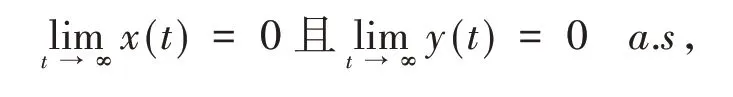
即食饵种群和捕食者种群以概率1呈指数灭绝.

证明 对于食饵种群，当t≥0时，x(t)为正解，由模型（1）可得

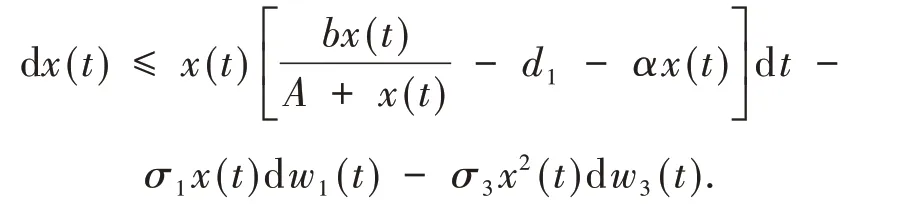
考虑函数f(x)=x[bx(A+x)-d1-αx]，其中x＞0.

①若αA≤0.5(d1-b)，函 数f在[0,∞)上单调递减，且最大值为f(0)=0.（证明过程见文献［5］定理3.2），则

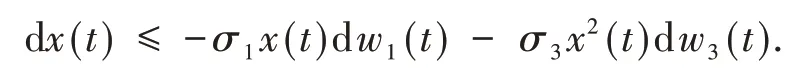
设ϕ(t)是下列方程的解.

由随机比较原理得，当t∈[0,∞)时，0≤x(t)≤ϕ(t) ,a.s.则 有 logx(t)≤logϕ(t)a.s.根据公式和式（9）得

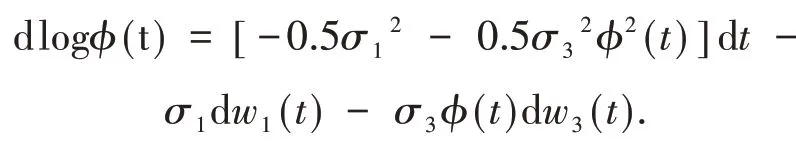
因此

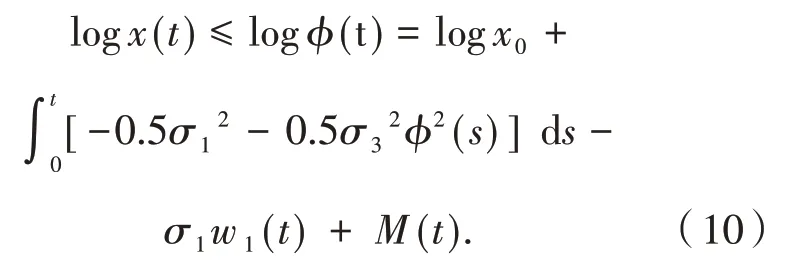
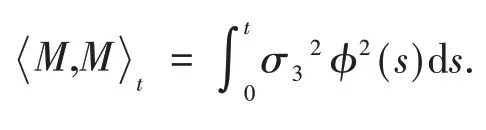
设n=1 , 2 , …，由指数鞅不等式［6］得

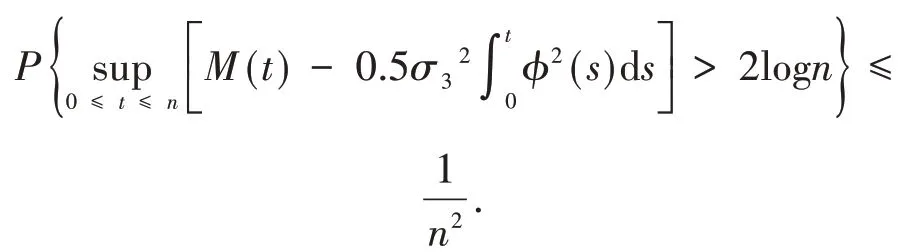
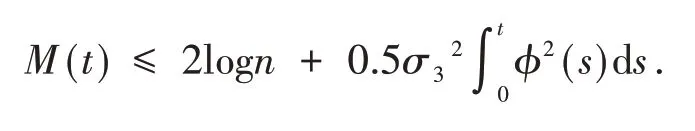
将上式代入式（10）得

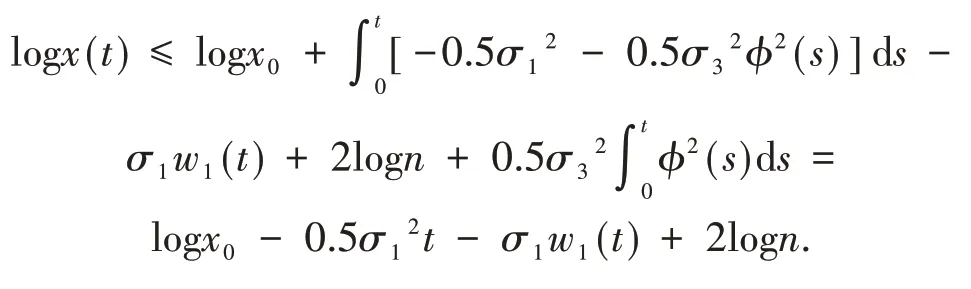
因此，对几乎所有ω∈Ω，若0＜n-1≤t≤n且n≥n0时，

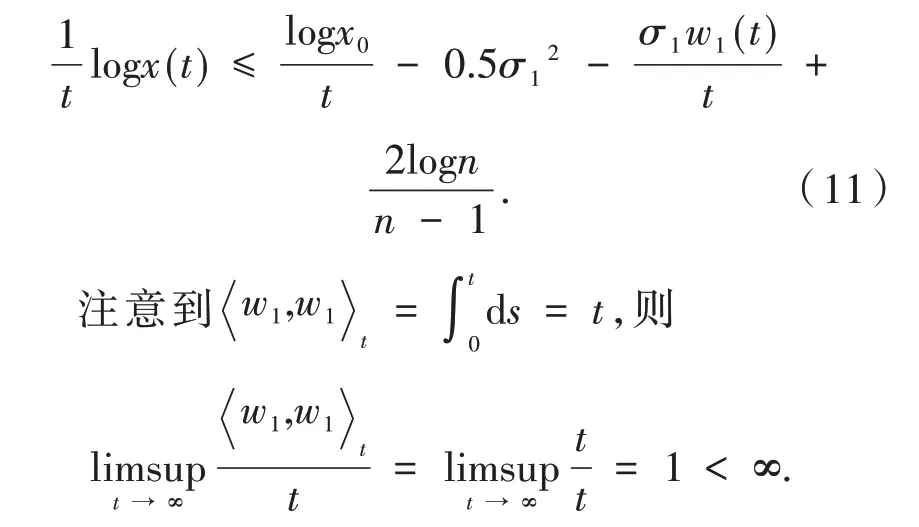
由强大数定律［6］可得

结合式（11）可推出

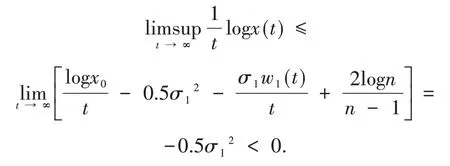
因此

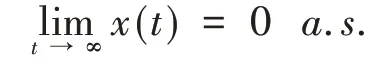
②当d1≤b时，则αA＞0.5(d1-b).αA≥b-d1，函数f在[0,∞)上单调递减，且最大值为f(0)=0（.证明过程见文献［5］定理3.2）因此，重复情形①的步骤可得αA＜b-d1且(b-d1-αA)2(b-d1+8αA)-27d1(αA)2＜0，函数f在[0,∞)上单调递减，且最大值为f(0)=0（.证明过程见文献［5］定理3.2）.同理有

③对logx(t)利用̂公式得

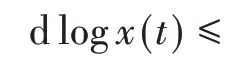
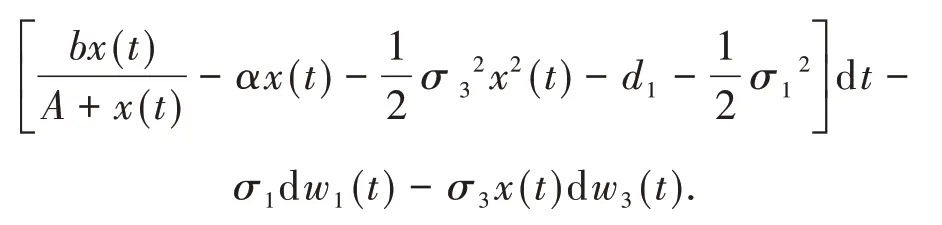
对上式两边分别从0到t积分得

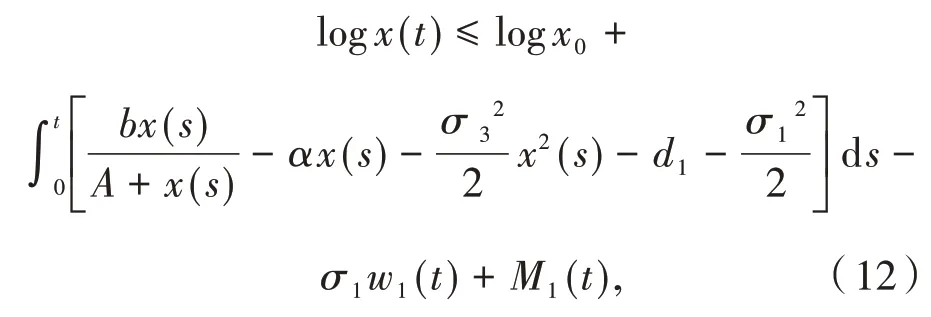
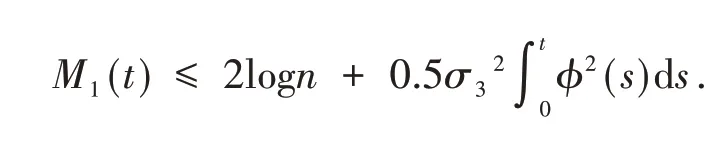
将上式代入（12）得

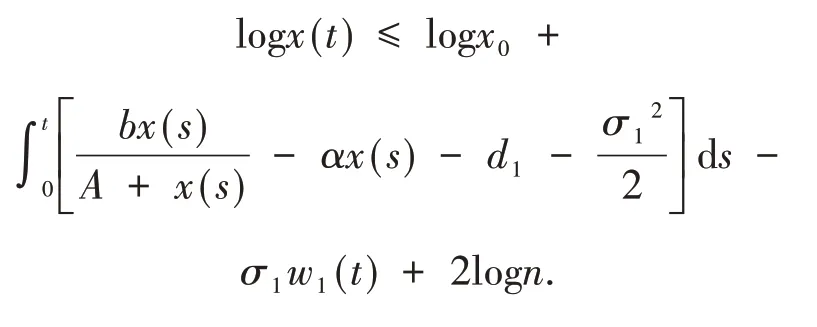
考虑函数f(x)=bx(A+x)-αx-d1-由αA1≤b得此时函数f取得最大值为因此，对几乎所有ω∈Ω，若0＜n-1≤t≤n且n≥n0有

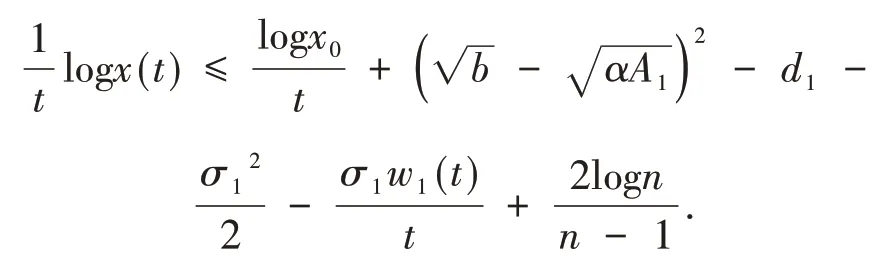
由定理条件及强大数定律得

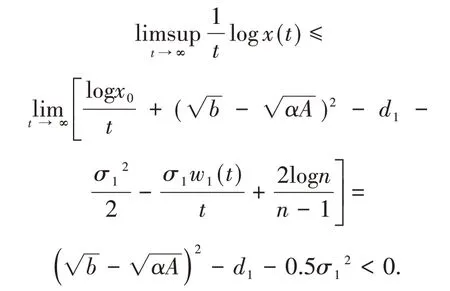
则

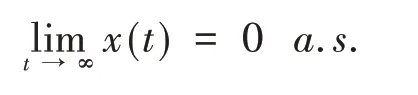
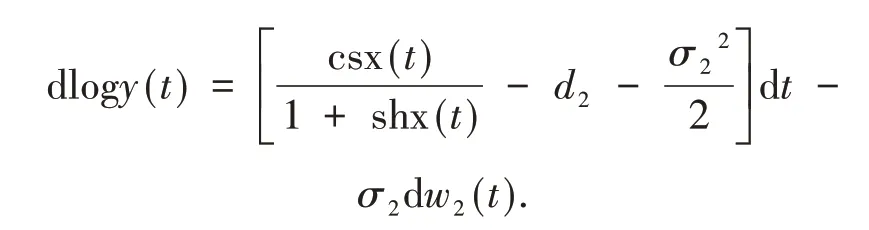
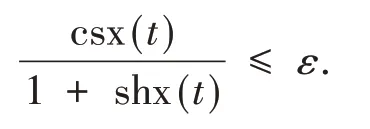
因此对任意t≥t0,ω∈Ωε，有

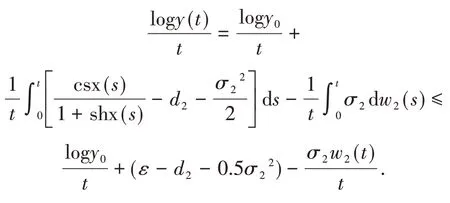
对上式运用强大数定律得

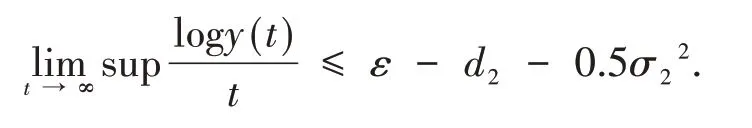
由ε的任意性，

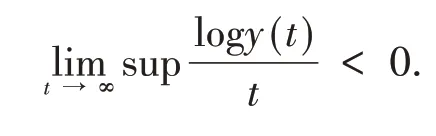
则

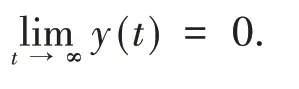
3 结语

本文讨论食饵具有Allee效应及双参数扰动的捕食-食饵种群的灭绝性，得到在一定条件下，食饵种群和捕食者种群以概率1呈指数灭绝的结论.并且当食饵种群灭绝时，捕食者种群一定会灭绝.

本文仅对模型正解的存在唯一性及种群灭绝性进行了研究，今后将对该模型的全局吸引性及其数值模拟等作进一步探究.