广义超几何函数定义的解析函数子类的性质

韩海燕

如何构造与广义超几何函数相关的各种有意义的解析函数类一直都是国际上比较活跃的一个研究方向.MILLER等在1991年发表了超几何函数的呈象性、凸性和局部单叶性［1］；2002年，DZIOK等利用从属方法研究了解析函数子类的凸半径、星象半径及系数估计等［2］；DARWIAH等在2009年利用从属定义了多叶解析函数类，并研究了其系数估计、极值点及凸半径等［3］.受其启发，本文利用卷积研究并得到广义超几何函数定义的某一解析函数类的有趣结论.

1 研究内容

定义1设ϕ(z)具有如下形式：

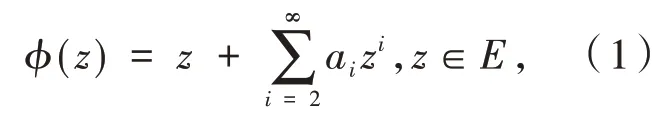
ϕ(z)在单位圆盘E={z∈Z:|z|＜1}内解析，设ℜ表示函数ϕ(z)所构成的函数类.函数ϕ(z)具有形式（1），ψ(z)具有如下形式：

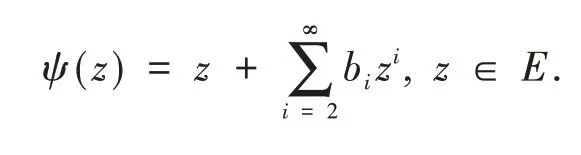
定义(ϕ*ψ)(z)为ϕ(z)和ψ(z)的卷积，形式如下：

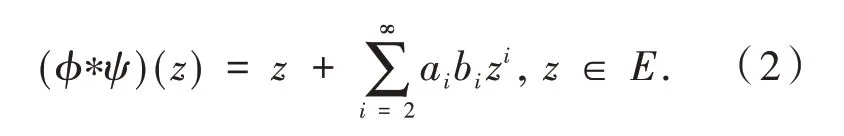
本文假设

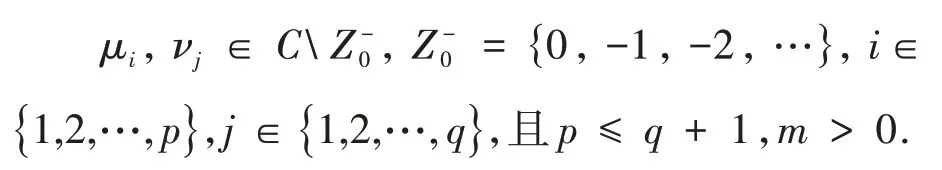
定 义2设 广 义 超 几 何 函 数PFq(μ1,…,μp;ν1,…,νq;z)为：

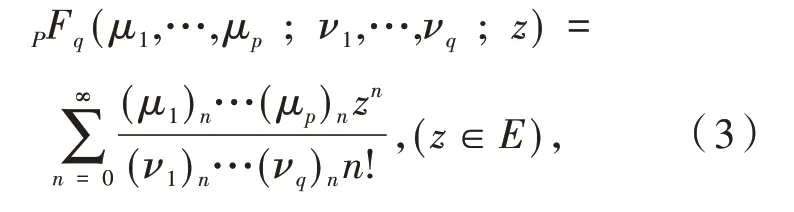
其中：p≤q+1，p，q∈N⋃{0}，N={1 ,2,3,…}.这里(η)n为记号，定义为：

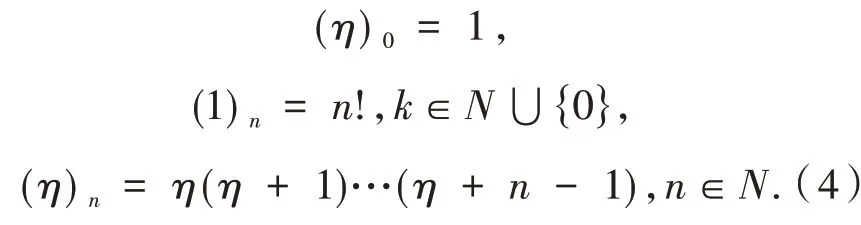
设 函 数G(μ1,…,μp;ν1,…,νq;z)可 表 示为：

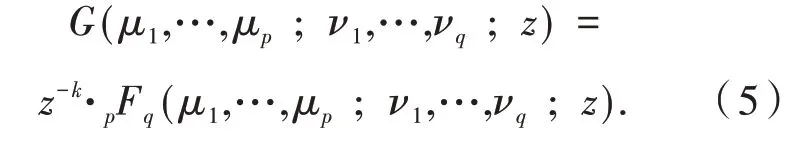
定义3利用卷积定义线性算子

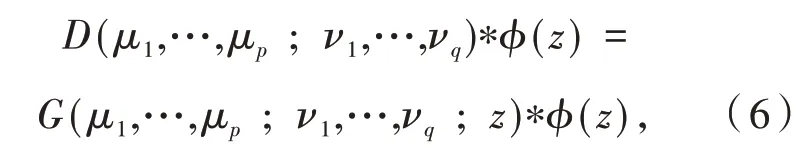
这里ϕ(z)在去心单位圆盘E0=E{0}内解析，且具有如下形式：

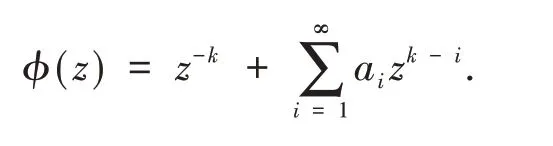
定义4定义函数ℵ(μ1,…,μp;ν1,…,νq;z)为：

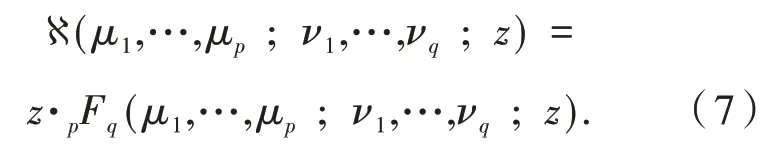
令函数ℵm(μ1,…,μp;ν1,…,νq;z)为：

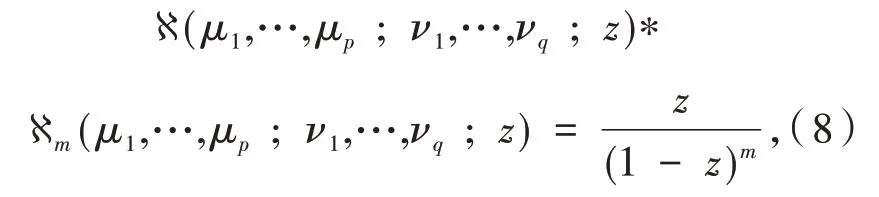
其中：m＞0.

定义5类似于定义线性算子D(μ1,…,μp;ν1,…,νq;z)的方法，在ℜ上定义线性算子Dl(μ1,…,μp;ν1,…,νq;z)，形式如下：

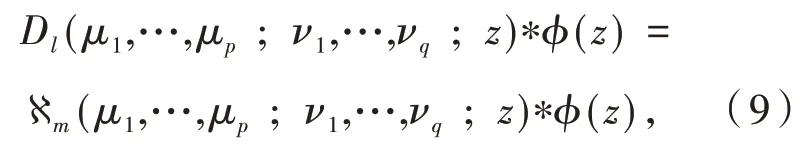
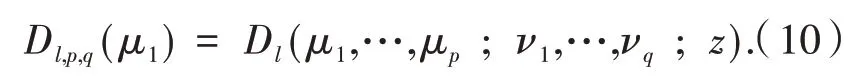
于是从式（8）、式（9）、式（10）易证明微分公式

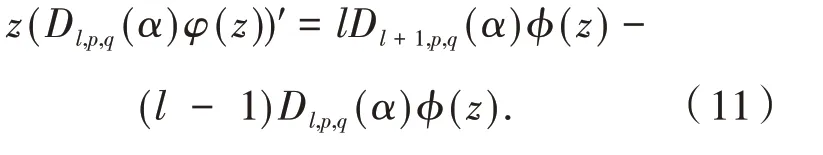
定义6［4-6］设f(z)在单位圆盘E内解析，满足f(0)=1，且

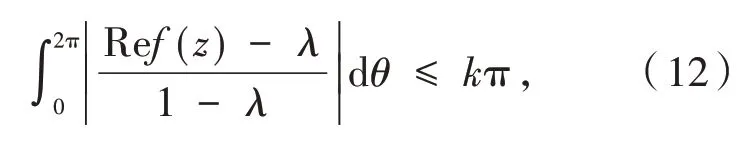
这 里：z=reiθ，k≥2，0≤λ＜1，那 么 称 函 数f(z)在 函 数 类Ωk(λ)内.此 外，记Ω(λ)=Ω2(λ)，表示实部大于λ的解析函数类.

说明：（i）易证得上述函数f(z)∈Ωk(λ)⇔存在f1，f2∈Ωk(λ)，使得

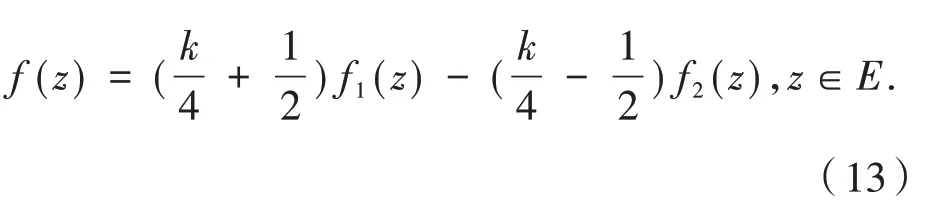
（ii）Ωk(λ)是凸集.

定义7设0≤λ＜1，c＞0，b∈C且Reb≥0，函数ϕ(z)∈ℜ满足

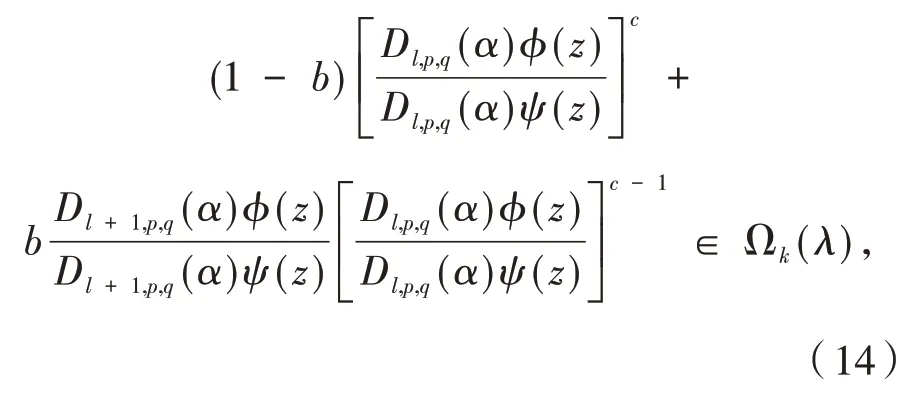
其中：k≥2,ψ(z)∈ℜ，且满足

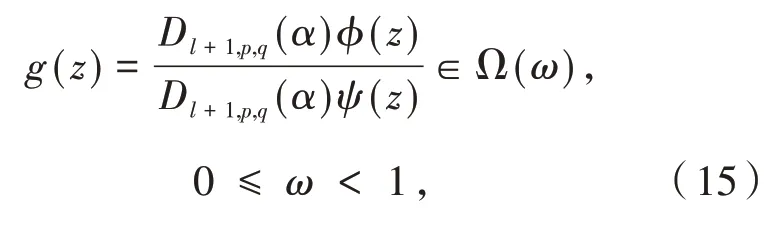
那么函数ϕ(z)在函数类(α,λ,c,ω,k)内.

为证明本文主要结论，需要下述引理.

引理1［7］设f(z)在E内解 析，f(0)=1，设ρ1∈C且Reρ1≥0，ρ1≠0，则

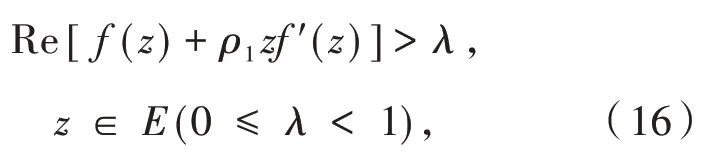
又

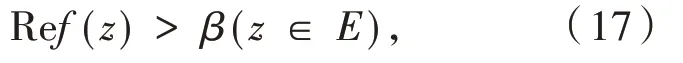
这里

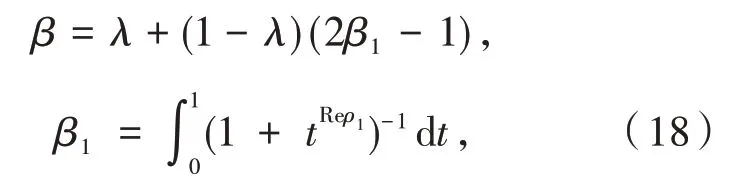
β1是Reρ1递增的函数，在某种意义上这个估计是准确的.

引 理2[8]设α=α1+iα1，β=β1+iβ2，ψ(α，β)是复函数，且满足下列条件：

（i）ψ(α，β)在域D⊂C2内连续；

（ii）(1,0)∈D且Reψ(1,0)＞0；

2 主要结论

定 理1若b＞0，则

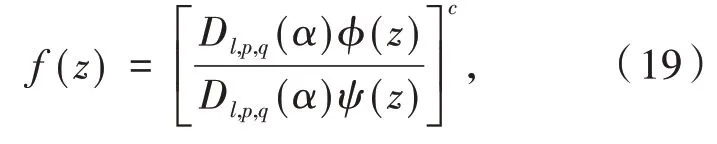
其中：f(0)=1，ψ(z)在E内解析，f(0)=1，ψ(z)满足条件（15），从说明（i）中可以得出ϕ(z)∈(α,λ,c,ω,k)的充要条件是

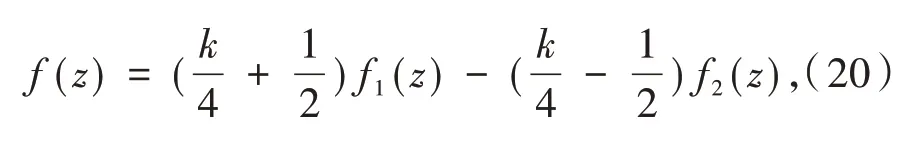
其中：f1(z)，f2(z)∈ Ω(λ).

根据微分公式（11）及式（15）可以得到如下结果.

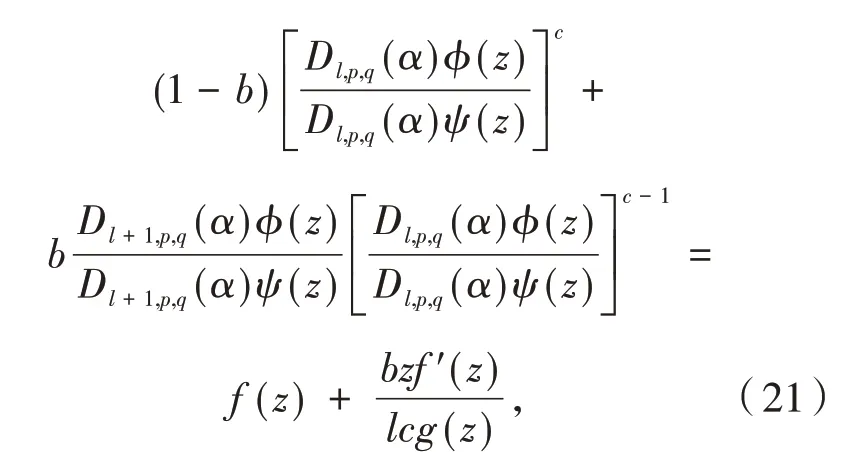
这里g(z)由式（15）给出.

由式（20）可以推导出：

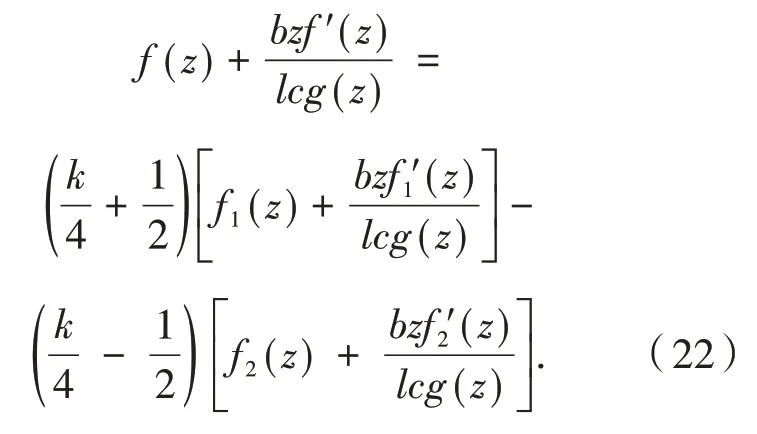
因为ϕ(z)∈(α,λ,c,ω,k)，从 式（21）和式（22）得出

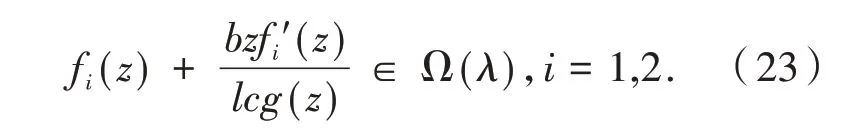
令Fi(z)=fi(z)-λ，i=1，2，上述式子变为：

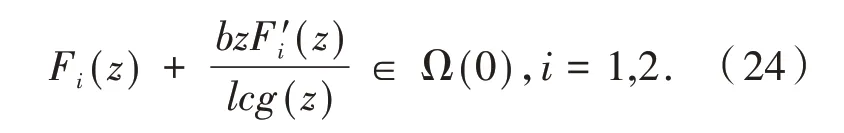
为了证明结论，需要证明式（26）包含Fi(z)∈ Ω(0)，i=1，2.定义函数ψ(α，β)，α=Fi(z)，β=zF′i(z)，故得到

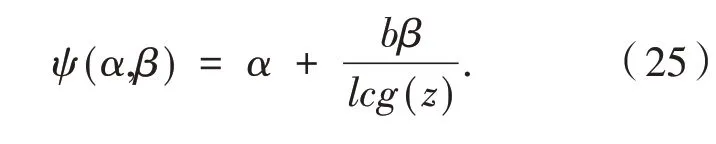
易发现ψ(α，β)满足引理2的条件（i），（ii）.因为g(z)∈ Ω(λ)，即Reg(z)＞λ，∀z∈E，0≤λ＜1，故当时，有

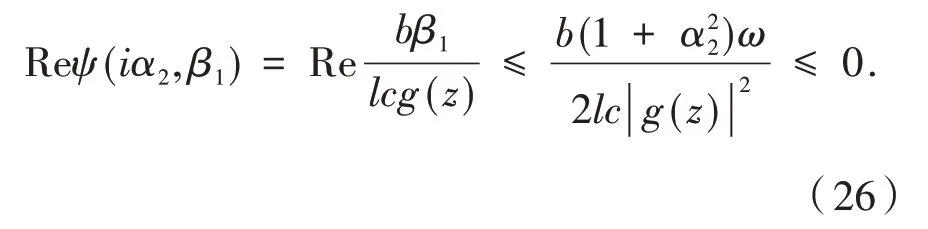
利用引理2，可以得出Fi∈Ω(0),i=1,2.

定 理2若0≤b1＜b2，则(α,λ,c,ω,k)⊂(α,λ,c,ω,k).

证明 设任意函数ϕ(z)∈(α,λ,c,ω,k)，令

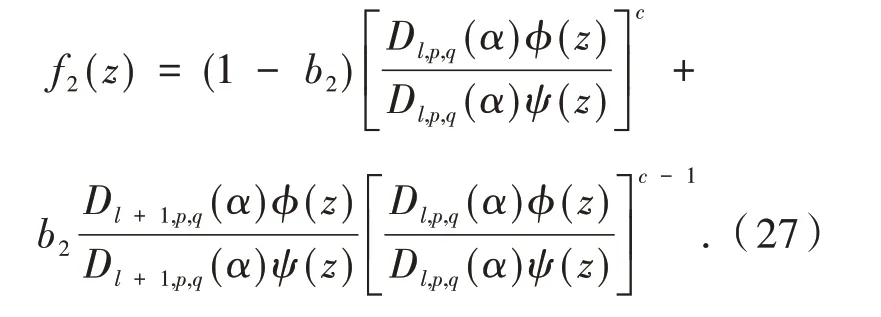
根据定理1，得到

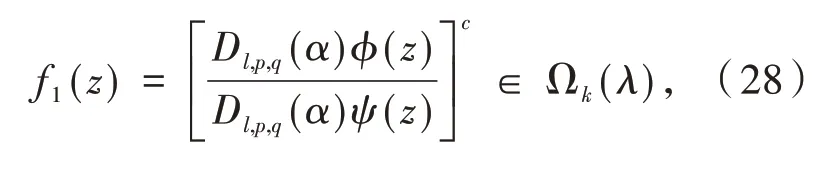
经计算

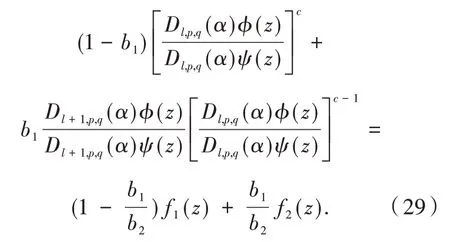
由说明（ii）知函数类Ωk(λ)是一凸集，故对于0≤b1＜b2，式（29）的右侧属于Ωk(λ)，即ϕ(z)∈(α,λ,c,ω,k).

为了证明下面定理，需要使用Bernardi定义的算子Ld，算子Ld为：

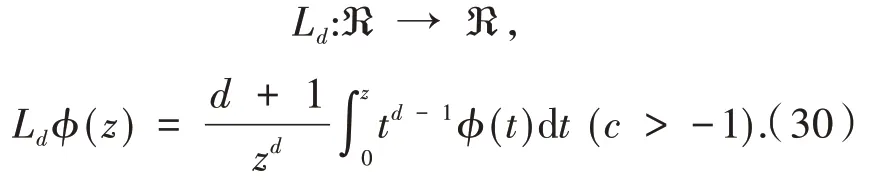
定理3若ϕ(z)∈ℜ，Ldϕ(z)由式（34）给出，设b∈C，且Reb＞0，则

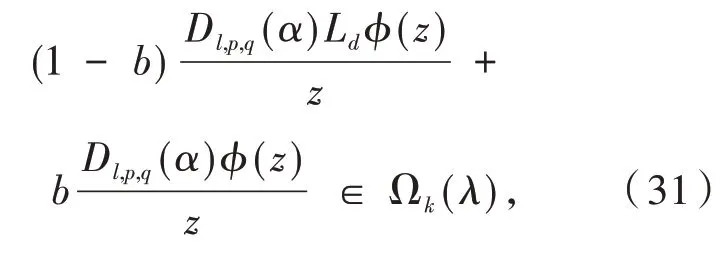
即

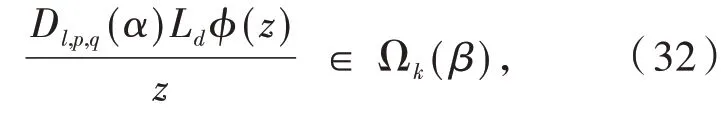
这里β是由式（18）给出，令

证明 对式（30）进行微分得到

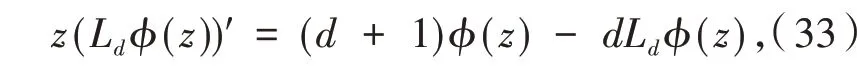
利用定义（9）得到

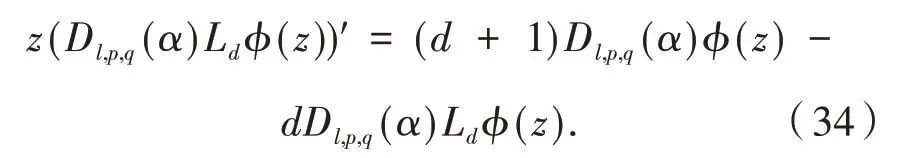
令

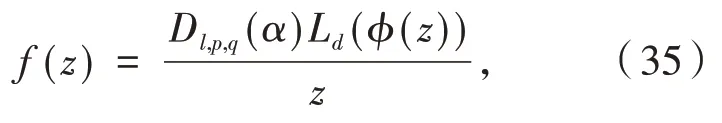
根据说明（i），那么需要证明f(z)具有如下形式：

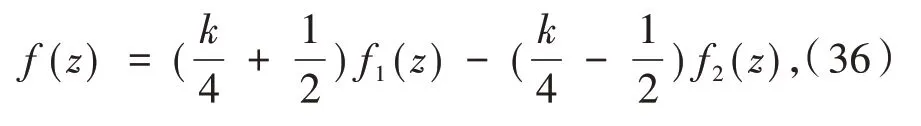
其中：f1(z)，f2(z)∈Ω(β).

综合式（34）～式（36），可以得到

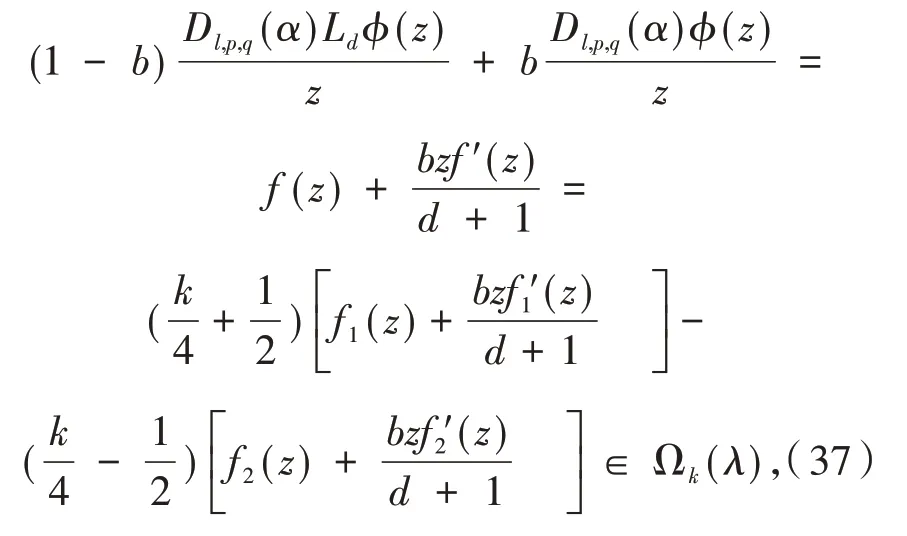
故从说明（i）看出

结合引理1，得出fi(z)∈Ω(β)，i=1，2，β由式（18）给出且

定 理4设b＞0,＜ω＜1，若ϕ(z)∈(α,0,c,ω,k)，则ϕ(z)∈(α,0,c,ω,k),|z|＜R，这里

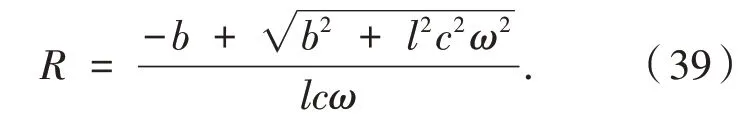
证明 令任意函数ϕ(z)∈(α,0,c,ω,k)，令

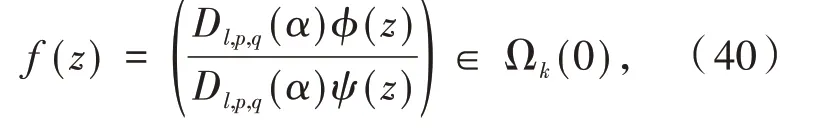
且ψ(z)∈ℜ满足条件

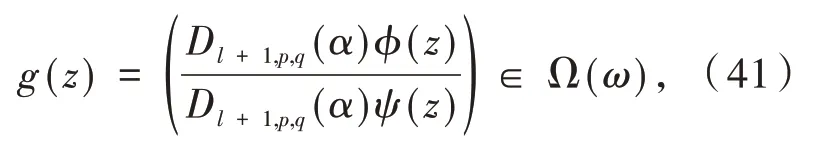
根据说明（i），式（40）成立当且仅当

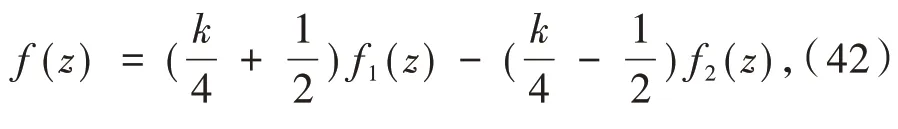
其中：f1(z)，f2(z)∈Ω(0)

类似于定理1的证明，可以得到

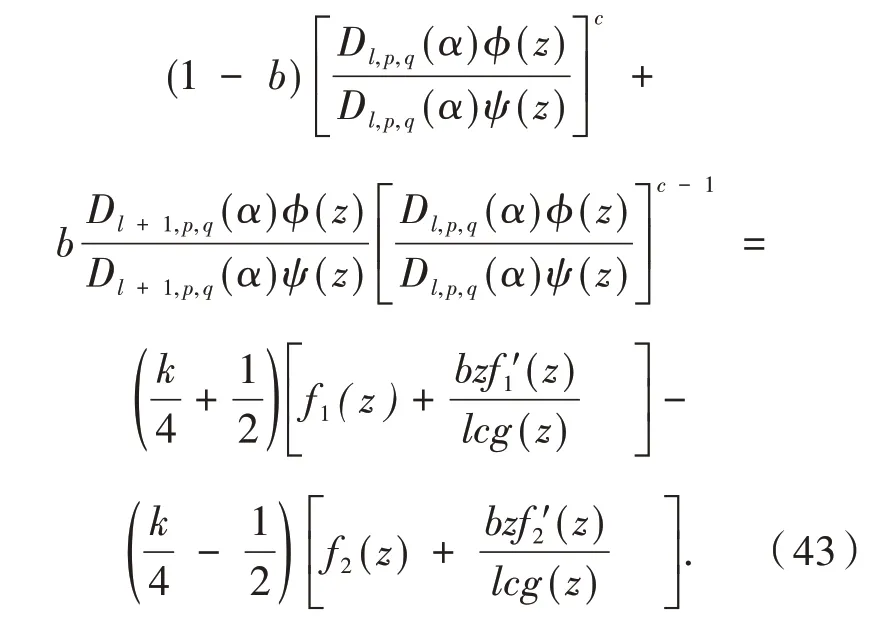
为了证明结论，需要估计R的值.

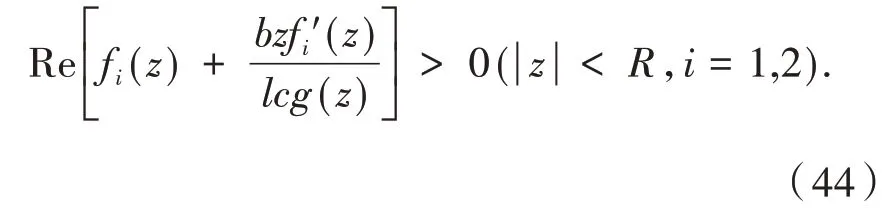
根据函数类Ω(0)的估计［9-10］，则有

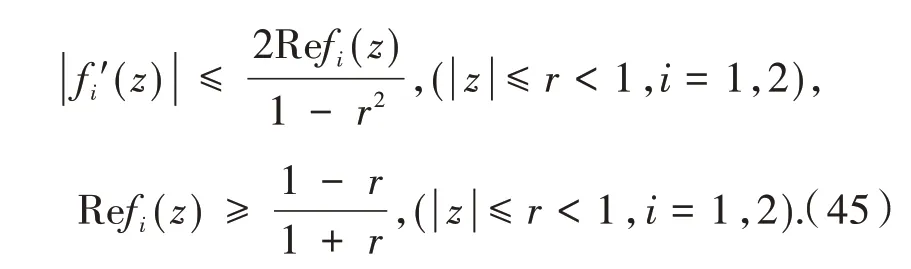
由式（41）得

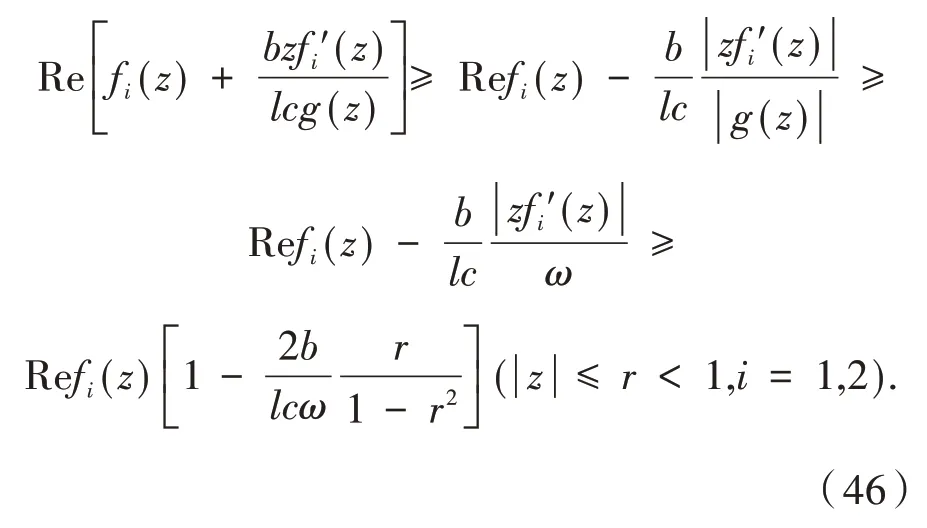
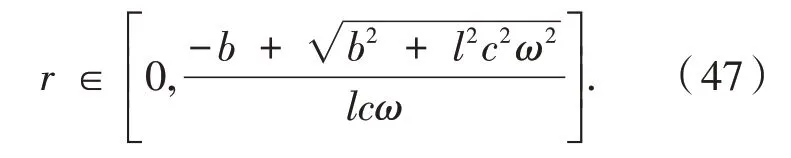
由式（46）和式（47）得到

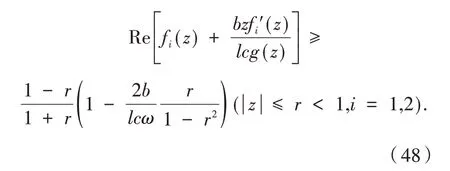
容易看出，上述不等式的右边大于或等于0的充要条件是

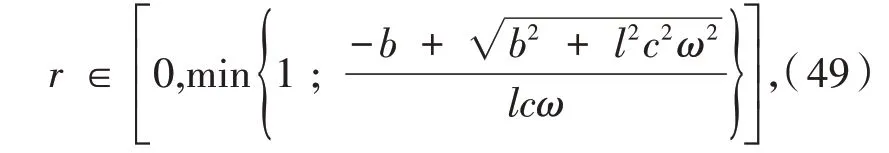
再根据式（47）即可证得结论.

3 结语

本文利用广义超几何函数得到一类新的解 析 函 数 子 类(α,λ,c,ω,k)，研 究 其 一 些 性质.本文给出新的解析函数类的构造过程，有利于广义超几何函数在几何函数理论中的研究.