径向振动匹配层换能器的设计参数及模态优化*

郭帅宏， 李 军， 王欢涛

(南京航空航天大学 机电学院, 南京 210016)

振动辅助研磨技术有效提高了研磨效率及被研工件表面质量与尺寸精度，广泛应用于兵器、船舶、核工业及航空航天等领域[1-3]。换能器作为振动辅助研磨系统的核心装置，产生的高频振动带动游离或固结的磨料及研磨液不断划擦、冲击被研工件表面，以达到高效去除材料的目的[4]。换能器内部结构形式、元件尺寸及材料性能参数等都是影响振动辅助研磨加工效率和表面质量的重要因素。

WANG等[5]提出了基于传递矩阵模型的夹心式纵向振动换能器，通过传递矩阵计算出换能器的频响特性及耦合振动特性，证实了传递矩阵模型的有效性。ZHANG等[6]推导了纵向振动换能器的机电耦合模型，获得了换能器的共振频率及各阶振型，其将能量法和等效电路法相结合，得出了压电陶瓷尺寸对机电耦合系数和共振频率的影响规律。刘泽宇[7]利用解析法设计谐振频率为35 kHz的纵向振动换能器，通过等效电路法分析电感对压电振子的影响，并推导出频率方程，验证了电路匹配理论的正确性。

夹心式纵向振动换能器虽用途广泛，但其受限于四分之一波长理论(轴向尺寸不得得超过四分之一波长)，在高频工况下，换能器的轴向厚度、质量、体积均过小，致使其加工、紧固困难。压电陶瓷片共振引起的非线性问题导致换能器辐射功率与声波辐射面积不足，电声转化效率不够理想，加之纵向振动换能器易造成被研工件厚度方向的尺寸偏差和表面缺陷，严重影响了超声研磨质量[8]。为满足振动辅助研磨要求，一种夹心式径向振动超声换能器逐渐成为研究热点。这种换能器结构简单、工作频域广、声辐射面积大且半径方向辐射均匀，可以很好地保证工件研磨质量[9-12]。

LIU等[13]分析了金属薄壁圆柱壳和压电陶瓷薄壁圆管的径向振动，基于等效电路和径向振动边界条件，推导出径向振动换能器共振频率、反共振频率、机电耦合系数与几何尺寸之间的关系。LIN[14]设计了一种新型复合压电陶瓷换能器，此换能器由在厚度方向极化的压电陶瓷细环和金属细圆环组成，通过仿真分析得出径向振动换能器发射效率高且径向声辐射均匀的结论。

夹心式径向振动换能器外壳为铝合金材料，但铝合金声阻抗较大，难以保证在各种工况下的传声效率。针对这一问题，基于匹配层外壳的压电换能器技术得到迅速发展，并逐渐成为提高换能器工作性能的主流技术[15-16]。匹配层外壳有效提高了压电换能器电声转化率、能量透射率、工作带宽、分辨率和灵敏度，且保证换能器工作时不受外界环境污染，大大改善了换能器的工作性能[17]。

为提高夹心式径向振动换能器的电声转化率和能量透射率，设计基于匹配层外壳的径向振动压电换能器，分析匹配层材料、换能器直径、压电振子厚度对换能器工作性能的影响，并结合不同设计频率下的最佳模态振型优化换能器设计参数。

1 径向振动匹配层换能器设计

1.1 压电振子及匹配层材料选取

压电振子作为换能器的核心元件，其材料参数是影响换能器工作性能的重要因素。PZT-4(发射型)压电陶瓷因其电声转换能力高、介电损耗小、可加工性及经济性好，被广泛应用于发射型压电超声换能器中。

PZT-4压电陶瓷材料的密度ρ=7 500 kg/m3。

刚度(N/m2)矩阵：

[C]=

(1)

介电常数(F/m)矩阵：

(2)

压电(C/m2)矩阵：

(3)

匹配层作为换能器辐射端有效匹配2种介质声阻抗的中间均匀层，在保护换能器不受外界环境污染的同时，大大提高了换能器的电声转化率、能量透射率及灵敏度，并拓宽了换能器的工作频域。随着对匹配层模型的不断研究，学者们提出了诸多理论以确定匹配层声阻抗值。其中，传统理论作为最常用的理论模型被广泛应用于各类工程领域中，其表述如下：

假设介质1的声阻抗为Z1，介质3的声阻抗为Z3，当忽略介质吸收的影响，且匹配层厚度为λ/4的(λ为声波在匹配层中的传播波长)奇数倍时，匹配层声阻抗Z2可表示为：

(4)

根据空气介质匹配层换能器的结构及声波传输机理可得，介质1为PZT-4压电陶瓷，其声阻抗约为30.00×106kg/(m2·s-1)，介质3为空气，其声阻抗约为440.00 ×106kg/(m2·s-1)，根据传统理论的计算公式可求得匹配层的声阻抗约为0.11 ×106kg/(m2·s-1)，但实际生产中无法制备出声阻抗如此低的固体匹配层。在环氧树脂基材中添加一定量的空心玻璃微珠制备空气耦合声匹配层，匹配层的密度、声速和声阻抗(声阻抗等于密度与声速之积)可随空心玻璃微珠性能参数及结构参数的改变而改变，使用此方法制备而成的树脂基匹配层的最小声阻抗约为1.18 ×106kg/(m2·s-1)(密度约为540 kg/m3，声速约为2 200 m/s)[18]。

1.2 径向振动匹配层换能器总体设计

径向振动匹配层换能器示意图如图1所示：1为树脂基匹配层外壳；2为性能参数一致的径向极化PZT-4压电陶瓷环组，其工作模式可按环组直径方向的准厚度振动处理；3为膨胀内芯环组，起到固定压电陶瓷环组的作用。a、b、d分别为PZT-4压电陶瓷环组、匹配层外壳及膨胀内芯环组内径，c为径向振动匹配层换能器外径。通过外加电场的作用，径向振动匹配层换能器可产生沿径向的高频振动。

图1 径向振动匹配层换能器示意图Fig. 1 Schematic diagram of radial vibration matching layer transducer

在径向振动匹配层换能器中，匹配层外壳的厚度为λ/4时(λ为声波在匹配层中的传播波长)，匹配层换能器的工作效率最高。超声换能器的匹配层外壳材料为空心玻璃微珠和环氧树脂混合制成的复合材料，声波在此匹配层中的传播速率为2 200 m/s，波长的计算公式为：

(5)

式中：c=2 200 m/s，f为匹配层超声换能器工作频率。空气介质径向振动超声换能器的工作频率一般在25～35 kHz，故在范围内选定27、30和34 kHz等3个工作频点。声波在匹配层外壳中的传播波长求解分别为81.5、73.3和64.7 mm,λ/4分别为20.375、18.325和16.175 mm。因此，对匹配层外壳厚度l1分别为20、18和16 mm的树脂基进行超声换能器设计。

根据径向振动匹配层换能器示意图及实物模型，对径向振动匹配层换能器进行设计，如图2所示(螺栓螺母、电极片等结构省略)：换能器轴向高度为60 mm，树脂基匹配层外壳厚度l1分别为20.0、18.0和16.0 mm。在PZT-4压电陶瓷环组厚度的设计方面，考虑到压电陶瓷太薄不易于声波传播，太厚又不利于激振，一般设计厚度为5～10 mm，故选取PZT-4压电陶瓷环组厚度l2分别为5.0、7.5、10.0 mm。同时，考虑到研磨盘的直径及研磨效率，径向振动换能器的直径一般为100～150 mm，对直径D分别为100、125、150 mm的换能器进行设计。通过对径向振动匹配层换能器的仿真分析，探究各尺寸参数对换能器工作性能的影响，并选出匹配层压电换能器的最佳设计尺寸。

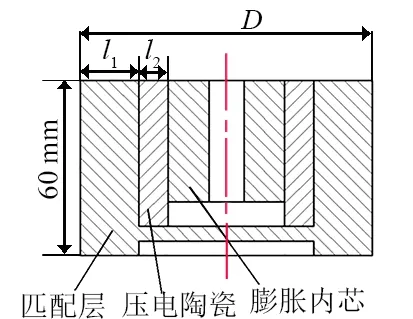
图2 径向振动匹配层换能器剖视图Fig. 2 Sectional view of radial vibration matching layer transducer

2 匹配层换能器参数优化

径向振动匹配层换能器在其谐振频率(即共振频率)处时，其振动性能被充分激发，发射效率最高。通过ANSYS有限元分析软件对匹配层-压电振子系统进行模态分析，归纳出匹配层材料参数、换能器直径、压电振子厚度对换能器工作性能的影响，并确定在设计工作频率下径向振动匹配层换能器的最佳设计尺寸及模态振型。

2.1 匹配层材料参数的影响

为研究匹配层材料参数对换能器工作性能及仿真结果的影响，保持匹配层外壳厚度20、18和16 mm，压电陶瓷环组厚度5.0、7.5、10.0 mm，换能器直径100、125、150 mm不变，仅改变匹配层材料参数进行模态分析。传统的径向振动换能器外壳为铝合金材料，密度ρ=2 700 kg/m3,声速v=6 260 m/s，声阻抗Z=16.90 ×106kg/(m2·s-1)。其模态分析结果如图3所示，在分析频率范围内共有三阶谐振模态，其固有频率(谐振频率)分别为27 129、27 131、27 155 Hz。压电振子虽充分激振，但铝合金外壳几乎没有形变与振幅，无法将压电振子振动所产生的声能传递到外界的空气介质中。由此可得，传统径向振动换能器在空气介质中工作时，其铝合金外壳不能有效地对压电振子及空气介质进行声阻抗匹配，换能器振动的能量难以传递到空气介质中，导致电声转换率和能量透射率较低。

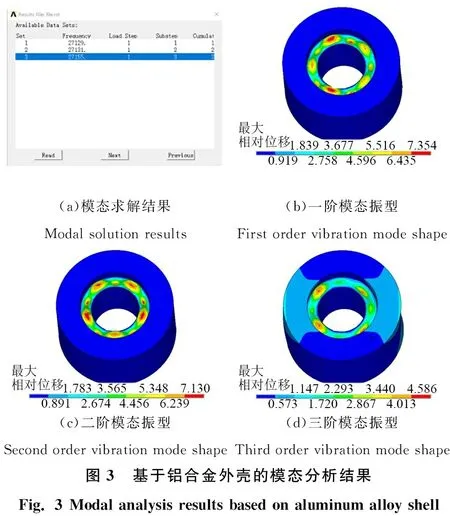
(a)模态求解结果Modal solution results(b)一阶模态振型First order vibration mode shape(c)二阶模态振型Second order vibration mode shape(d)三阶模态振型Third order vibration mode shape图3 基于铝合金外壳的模态分析结果 Fig. 3 Modal analysis results based on aluminum alloy shell

径向振动匹配层换能器外壳为树脂基匹配层材料，密度ρ=540 kg/m3,声速v=2 200 m/s，声阻抗Z=1.18 ×106kg/(m2·s-1)，其仿真结果如图4所示。

(a)一阶模态振型First order vibration mode shape(b)二阶模态振型Second order vibration mode shape图4 基于树脂基匹配层外壳的模态分析结果 Fig. 4 Modal analysis results of shell based on resin based matching layer

分析频率范围内共有二阶谐振模态，其固有频率(谐振频率)分别为27 125、27 181 Hz。与铝合金外壳相比，树脂基匹配层外壳可有效地对压电振子及空气介质进行声阻抗匹配，故在二阶模态中，树脂基匹配层都发生较为可观的形变，从而高效地将压电振子产生的能量传递到空气中，提高了换能器的空气介质中的电声转换率和能量透射率。

2.2 换能器直径的影响

在27 kHz的设计工作频率下，为研究换能器直径对仿真结果的影响，保持匹配层外壳厚度20、18和16 mm和压电陶瓷环组厚度5.0、7.5、10.0 mm不变，仅改变换能器直径进行模态分析。根据设计，换能器的直径分别为100、125、150 mm。图5为换能器直径是125 mm时的典型模态振型图。

(a)二阶模态振型径向视图Radial view of second order(b)三阶模态振型径向视图Radial view of third order(c)二阶模态振型轴向视图Axial view of second order(d)三阶模态振型轴向视图Axial view of third order图5 典型模态振型图 Fig. 5 Typical modal vibration shape diagram

通过对比可知：换能器直径增大后，由于匹配层厚度并未改变，但其泊松比较大且刚性较差，且径向变形总与纵向变形互相耦合，致使其径向与纵向变形加大，影响了换能器工作时的稳定性。同时，如图5所示，换能器直径增大后，其多个谐振模态中压电振子和匹配层并未充分激振，振幅、变形均较小，不能满足换能器设计要求。综上，换能器直径越小越有利于压电振子能量的聚集与传播，且其耦合变形较小，工作更加稳定，故在27 kHz的设计工作频率下，换能器直径最优值应取设计尺寸中的最小值100 mm进行匹配层换能器的总体设计。

2.3 压电振子厚度的影响

在设计工作频率27 kHz下，为研究压电振子厚度对仿真结果的影响，保持匹配层外壳厚度20、18和16 mm和换能器直径100、125、150 mm不变，仅改变压电振子厚度进行模态分析。压电振子厚度分别为5.0、 7.5、10.0 mm。

在共振频率下，匹配层换能器的激振越剧烈，振幅越大，工作性能越好。总体分析压电振子厚度对匹配层换能器每阶模态下最大振幅的影响，分别提取不同厚度下每一阶模态的最大振幅。按照仿真的结果，当匹配层厚度为5.0 mm时，其每阶最大振幅分别为2.29、1.76、1.49、1.67、1.66和1.61 mm；当匹配层厚度为7.5 mm时，最大振幅分别为1.46和1.64 mm；当匹配层厚度为10.0 mm时，最大振幅分别为2.32、 1.76、1.45、1.63、1.64和1.64 mm。

图6为压电振子厚度对换能器最大振幅的影响。如图6所示，在压电振子厚度逐渐变大的情况下，匹配层换能器的最大振幅并没有明显变化，可见增加压电振子的厚度并不能提高匹配层换能器的工作性能。

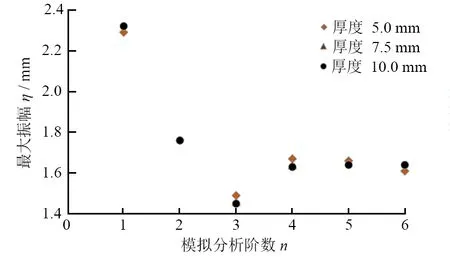
图6 压电振子厚度对换能器最大振幅的影响Fig. 6 Influence of piezoelectric vibrator thickness on the maximum amplitude of transducer

图7为压电振子厚度对各阶固有频率的影响。如图7所示，在工作频率为27 kHz时，随着压电振子厚度不断减小，其每一阶固有频率都不同程度地向上偏移，同时，每个厚度下的最佳振型只有一个，致使在不同厚度时最佳振型下的固有频率(27 094、27 180、27 342 Hz)不断远离设计频率。

图7 压电振子厚度对各阶固有频率的影响Fig. 7 Influence of piezoelectric vibrator thicknesson natural frequencies

虽然压电振子的厚度变化对换能器总体的最大振幅没有影响，但随着压电振子厚度不断减小，换能器的工作表面的最大振幅逐渐减小，即压电振子厚度减小降低了换能器工作表面的激振效果与工作性能。综上所述，压电振子最优厚度值应取设计尺寸中的最大值10.0 mm进行匹配层换能器的总体设计。

2.4 设计频率下最优尺寸及振型选择

在设计频率为27 kHz时，通过改变换能器尺寸参数并进行分析，可得最优压电振子厚度为10.0 mm，最优换能器直径为100 mm。图8为不同设计频率时的最佳振型图。如图8a所示：按照仿真结果，在此设计尺寸下，匹配层-压电振子系统的最优振型出现在第三阶固有频率处(27 094 Hz)。当换能器工作频率为30 kHz(图8b)和34 kHz(图8c)时，可以得到相同的结论。

(a)f1=27 kHz(b)f2=30 kHz(c)f3=34 kHz图8 不同设计频率时的最佳振型图Fig. 8 Optimum vibration mode shape diagrams at different design frequencies

当频率为27 kHz时，虽然其最佳轴向振型较均匀，但其匹配层外径处最大位移与最小位移有一定交叠，影响了换能器的径向激振性能；当频率为30 kHz时，其最佳振型虽与前者相似，但其径向和轴向变形并不均匀，纵径耦合振动较强，影响了换能器工作的稳定性；当频率为34 kHz时，匹配层-压电振子系统能够高效地向外传递压电振子径向振动产生的能量，使得匹配层外径边缘呈现最大振动位移，且此位移较均匀，能保证压电换能器工作的稳定性，匹配层轴向变形平缓且呈较为均匀的径向振动形式，纵径耦合振动较小，换能器径向振动被充分激发，符合径向振动设计要求。

如图9所示，在工作频率为34 kHz时，径向振动匹配层换能器匹配层厚度为16 mm，压电振子厚度为10.0 mm，换能器直径为100 mm。在谐振频率为34 729 Hz时，其工作性能最优。

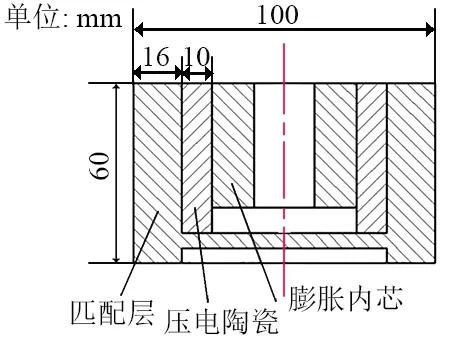
图9 径向振动匹配层换能器最佳设计尺寸Fig. 9 Optimum design size of radial vibration matching layer transducer

3 结论

设计基于匹配层外壳的径向振动超声换能器，研究匹配层材料、换能器直径、压电振子厚度对工作性能的影响，结果如下：

(1)换能器直径减小后，更利于压电振子能量的聚集与传播，且换能器耦合形变较小，工作更加稳定。因此，优化后所得换能器直径为100 mm。

(2)压电振子厚度减小后，换能器工作表面激振性能降低，且每一阶固有频率不同程度向上偏移，致使在不同厚度时最佳振型下的固有频率不断远离设计工作频率。因此，优化后所得压电振子厚度为10.0 mm。

(3)当工作频率为27、30、34 kHz时，最优压电振子厚度和最优换能器直径均为10.0 mm和100 mm。

(4)当径向振动匹配层换能器匹配层厚度为16 mm，压电振子厚度为10.0 mm，换能器直径为100 mm，且工作在第三阶谐振频率34 729 Hz时，其工作性能最优，振动辅助研磨效果显著提高。