短码元长度长波ASK信号的一种混沌检测方法*

（海军航空大学信号与信息处理山东省重点实验室 烟台 264001）

1 引言

对于对潜通信而言，其性能直接决定了战术指令的下达，进而决定了战争的走向，因此对于对潜通信的研究十分迫切。由于对潜通信处于海水的环境下，常规大气通信使用的中短波信号及其检测方法将不再适用［1］，而混沌振子以其对低频信号的敏感、强噪声下的优良检测性能［2］，开始被应用于对潜通信当中。文献［3］系统的归纳了ASK信号的混沌检测方法，并从能量的角度解释了其抗噪原理，但由文献［4］可知，混沌振子数字信号时对其载波的时频积存在下限要求，在天线驻波比曲线的特点及无码间串扰的要求下，某些带宽对应的码元长度可能小于该下限要求而无法被检测。本文正是在此背景下，根据混沌振子跳变的特点，提出了一种“嫁接”法产生待测序列的方法，并且考虑到扩展时频积不可避免地带来的计算量增大的问题，构造了新的混沌判决依据，从而减少了计算量。

2 ASK信号的混沌检测原理

Duffing振子是一个典型的非线性混沌振子，大量的研究验证了它能够产生混沌现象［5～7］，且自学者Birx将其应用到信号检测以来，已有大量的应用［8］。本文将通过该振子对ASK信号进行检测。Duffing振子的动力学方程为

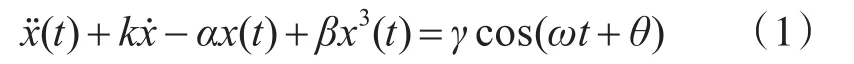
图1 分别输入0、1时Duffing振子相轨迹图

此时二者的相轨迹图有明显的区别，即可对两种码元做出判断。而当单个码元时频积不够时振子的相轨迹图如图2所示。

从图2中无法判断两个码元，这是因为混沌振子的相变过程是一个递推的过程［9～10］，时频积不足直接导致了递推过程无法不足从而未到达相变状态。

3 ASK信号的混沌检测原理

3.1 待测序列的产生

考虑到待测信号具有周期性，且在整个递推计算当中，只要保证积分步长h不变，延长时间长度将不会影响待测信号所携带的信号特征和整个递推过程。在此基础之上，考虑在接收端生成一组待测序列，该序列需保留足够的原始信号的信息，且需足够的时频积。实现以上两点最简单的方法就是周期延拓，但事实上，对接收到的信号周期延拓将会重复混入信号噪声，进而降低接收端能够检测的最低信噪比。因此拟采用一种类似“嫁接”的方法，即在原始载波信号的基础上对信号进行延拓。通过控制“嫁接”序列的幅值，在振幅键控信号载波频率对应最短时频积要求的基础之上，实现对信号的检测。

图2 单个码元时频积不够时振子的相轨迹图

在接收端生成n组待测序列，其中n为传输的波形种类数目，待测序列需满足以下三点要求：

1）“嫁接”序列频率与原始载波频率相同，且在已知此频率的条件下通过载波信号时间长度，计算“嫁接”序列的初始相位，保证待测序列相位连续。

2）“嫁接”完成后，序列的时频积为该频率下能够分辨混沌临界状态和大周期状态的最小时频积。

3）每组“嫁接”序列的幅值分别对应每个码元载波的幅值。

3.2 实现检测的判决依据

由混沌振子的敏感特性可知，大周期状态需保持每个点均处于大周期状态，否则某一个点进入混沌临界状态轨道就可能在接下来的递推过程中产生巨大的差别，导致最终状态出现差异［11］。因此，需保持原始载波与“嫁接”序列输入到Duffing振子得到的点均处于大周期状态的轨道时，才能进入大周期状态。

由以上分析过程可以得到以下两条结论：

1）当振子发生相变时，前端的载波幅值大于或者等于后端“嫁接”序列的幅值。

2）当振子不发生相变时，前端的载波幅值小于后端“嫁接”序列的幅值。

在以上两个结论的基础上，生成一个检测阵列，在检测过程中将每个待测序列对应输入到周期策动力的幅值为刚进入大周期状态的幅值减去待测序列中“嫁接”序列幅值的振子。将n-1组待测序列同时输入到n-1个Duffing振子组成的混沌阵列，利用传统的判决依据即可实现检测。但对于短码元长度数字信号而言，由递推过程可知，将码元时频积拓展到足够使得振子跳变时，会导致阵列中每个振子的运算次数增加，从而导致阵列故障率的增大。因此针对如何减小计算量的问题，需要一种新的判决依据，使得在较小计算量的条件下实现短码元长度数字信号的检测。

考虑到待测序列的时频积要保证振子发生相变，因此不能进一步减少其时间长度，进而减少每个码元检测时单个振子的运算次数。但传统判据而言，每个码元被检测时阵列中的所有振子都将进行运算，因此可以考虑从改进判决依据使用振子的数目出发，对于所有码元的检测过程而言，减少平均每个振子的运算量。

同样基于上述两条结论，按“嫁接”序列的幅值从大到小对待测序列进行排序（共n-1个序列，且n为偶数），然后将序号为奇数的待测序列输入到对应的振子，此时判决依据如下：

1）若所有振子均不跳变，则该码元为载波幅值最小时所对应的码元。

2）若所有振子均跳变，则该码元为载波幅值最大时所对应的码元。

3）若出现序号小于等于n的振子全部跳变，而大于n+2的振子均不跳变（n不为最大数）。此时该码元为“嫁接”序列序号为n或者n+1所对应的码元。此时只需再将“嫁接”序列序号为n+1所对应的待测序列输入到对应振子进行检测，若该振子跳变，则该码元为“嫁接”序列序号为n+1所对应的码元，若不跳变，则该码元为“嫁接”序列序号为n所对应的码元。

为避免每个码元检测时都使用序号为奇数的振子，造成单个振子故障次数与传统判据相比并未改变的问题，可以采用奇偶交换的方式对每个码元进行检测，即第一个码元采用序号为奇数的振子，第二个码元采用序号为偶数的振子，依此类推。序号为偶数的振子判决依据如下：

1）若所有振子均不跳变，将嫁接序列序号为n-1时所对应的待测序列输入到对应振子进行检测，若跳变，则该码元为嫁接序列序号为n-1所对应的码元，若不跳变则该码元为载波幅值最小时所对应的码元。

2）若所有振子均跳变，将“嫁接”序列序号为1时所对应的待测序列输入到对应振子进行检测，若跳变，则该码元为载波幅值最大时所对应的码元，若不跳变则该码元为“嫁接”序列序号为1时所对应的码元。

3）若出现序号小于等于n的振子全部跳变，而大于n+2的振子均不跳变（n不为最大数）。此时与序号为奇数的判据相同。

4 仿真实验

以8ASK信号为例，选取载波角频率为1rad/s，码元长度为24s，采用本文的检测方法对该数字信号进行检测，设置振子参数为ω=1rad/s，k=0.5，α=1，β=1 ，(x(0)，′(0))=(0，0)，且经二分法仿真可得到振子的γs=0.827，当采样率为0.01时，经仿真可得振子的最小时频积对应的时间长度均为24 π，以码元010（对应载波幅值为0.002）为例，若采用“嫁接”序列幅值为奇数时的待测序列，此时得到的待测序列如图3所示。

其对应的振子相轨迹图如图4所示。

由相轨迹图可以得到，“嫁接”序列幅值为0.001的待测序列并未使振子相变，而“嫁接”序列幅值为0.003、0.005、0.007的待测序列使得振子相变，因此该码元载波对应的幅值应为0.002或者0.003，只需再使用“嫁接”序列幅值为0.002的待测序列输入到振子检测即可。“嫁接”序列幅值为0.002的待测序列如图5所示。

其相轨迹图为图6。

此时该振子处于大周期状态，得到载波幅值为0.002，即实现码元11的检测。

将待测数字信号通过高斯白噪声信道，控制信号的信噪比，采用1000次蒙特卡洛算法计算本文判决依据与传统判决依据［12］的误码率，进行性能对比，具体结果如图7所示。

图3 本文方法产生的待测序列

图4 待测序列对应的相轨迹图

从图7中可以得到，两种判别依据在误码率性能上相近，即本文判别依据保留了Duffing振子在强噪声环境中对于微弱信号的检测能力。另一方面，针对8ASK信号而言，本文的判决依据检测一个码元使用了四个或者五个振子，而传统的判决依据需要七个振子，因此本文判决依据有更小的计算量，即本文判决依据条件下的接收机较传统检测依据条件下的接收机有更低的故障率。

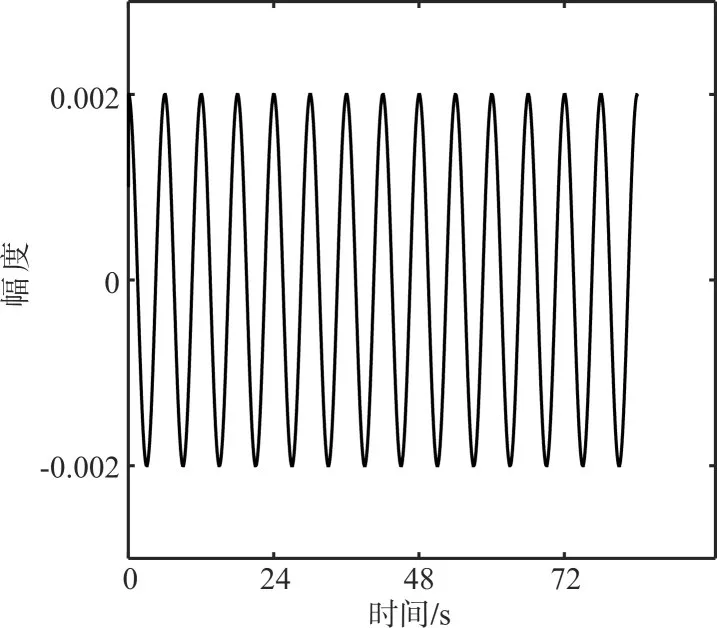
图5 “嫁接”序列幅值为0.002的待测序列

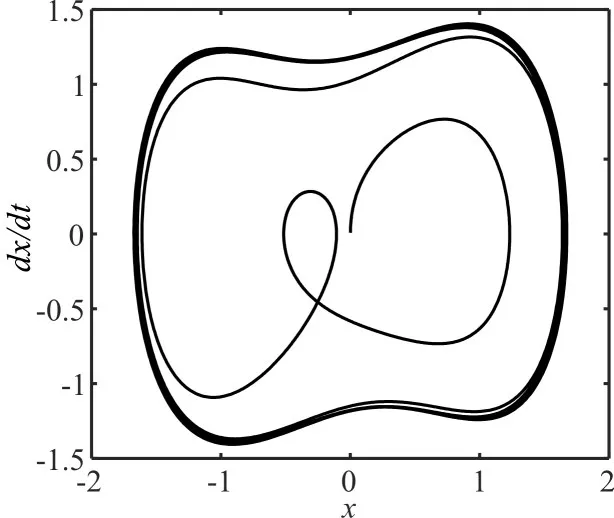
图6 “嫁接”序列幅值为0.002的待测序列对应的相轨迹图

图7 两种方法误码率与信噪比的关系

5 结语

本文提出了一种短码元长度长波ASK信号的检测方法，该方法基于混沌振子跳变时的特点，利用“嫁接”序列与原始载波序列之间的关系构造待测序列，并在此基础上构造了有更小计算量的混沌检测判决依据。仿真实验表明，该方法保留了混沌振子的优良检测特性，并且解决了拓展时频积导致的接收机故障率增大的问题。