用于水下探测的宽带超声换能器设计
刘晓晓,张 浩,曾 涛
(上海材料研究所 上海市工程材料应用与评价重点实验室,上海 200437)
迄今为止,声波是人类所发现的能在水中远距离传输信号和能量的唯一载体,现有的水声设备都依靠声波来传递信息[1]。利用声波可以完成水下目标的检测、识别、定位、通讯、导航、水中成像等[2]。水声换能器是声呐探测设备的核心部件,承担着信号发射和接收的使命,在水声探测领域发挥着重要作用[3]。
纵振换能器是水声换能器领域的一个分支,其设计理论成熟、制作工艺简单、性能稳定,在水下目标探测中有着广泛的应用[4]。为了能准确探测到障碍物位置并提前规避,使用的纵振换能器需具有低频、宽带、大功率等特性[5-6]。
目前,多模态振动耦合是拓宽纵振换能器工作带宽的有效方法之一,其能调整结构设计,使换能器中两种或两种以上的振动模态频率相距适中并有效耦合,达到拓宽带宽的目的[7]。常见的拓宽纵振换能器带宽的设计方法有纵弯、匹配层、单端激励、双激励、柔顺层等[8]。
笔者研制了一种可用于水下探测的宽带纵振换能器,采用双激励设计方法拓宽换能器带宽,并基于双激励夹心式换能器共振频率方程,对目标谐振频率为23,42 kHz的双激励纵振换能器进行了理论设计,然后通过有限元建模优化设计了一种双激励宽带纵振换能器,并制作测试了换能器样机。
1 双激励纵振换能器设计理论
1.1 双激励纵振换能器机电等效电路
双激励夹心式纵振换能器的典型结构示意如图1所示(图中R1,R2为半径;La为后盖板长度;Lm为质量块长度;Lb为前盖板长度;Le1,Le2分别为后晶堆与前晶堆的长度),其由两个金属圆柱、一个金属喇叭形前盖板和两组压电晶堆组成。压电晶堆由两个极化方向相反的压电晶片组成,压电晶片之间采用机械端串联、电端并联的方式相连接。两组压电晶堆与3个金属块通过应力螺栓相连接,在实际制备过程中,往往会在各部件连接面涂抹环氧胶,进一步加强部件间的连接。由于双激励夹心式换能器的长度可与波长相比,换能器中的压电晶堆振动模态可视为电场平行于长度方向的长度伸缩。

图1 双激励夹心式纵振换能器的典型结构示意
基于梅森等效电路和换能器的一维振动理论,可得到双激励夹心式纵振换能器的机电等效电路(见图2)[4]。图2中C1,C2分别为两组压电晶堆的一维截止电容,N1,N2分别为其机电转换系数,表达式分别为
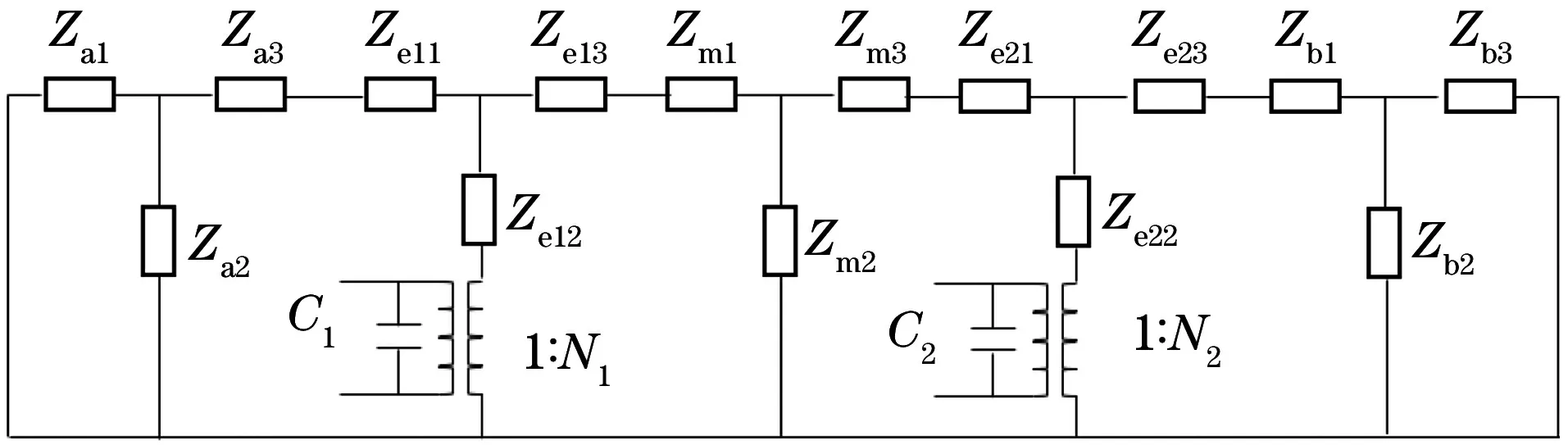
图2 双激励夹心式纵振换能器的机电等效电路
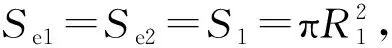
前后晶堆材料的纵向振动传播速度c0为

将图2进行多次的T型网络、Π型网络等效阻抗变换,可得到如图3所示的等效电路。图中Zq1,Zq2,Zq3为等效阻抗。
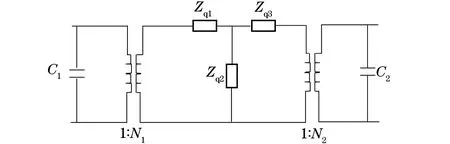
图3 双激励夹心式纵振换能器的简化等效电路
根据图3可计算得到整个双激励纵振换能器的输入阻抗Ze。根据换能器共振频率方程的定义可知,在共振频率下Ze=0,即换能器导纳曲线极大值对应的频率即为换能器共振频率点。
1.2 双激励纵振换能器共振频率方程
双激励换能器工作在低频时,前晶堆阻抗很大,近似于开路,其机械端n-N的反射阻抗ZnN为
式中:ω为角频率。
低频时的换能器机电等效电路如图4所示[11]。利用1.1节的方法,可得到低频前晶堆开路情况下换能器的共振频率方程为
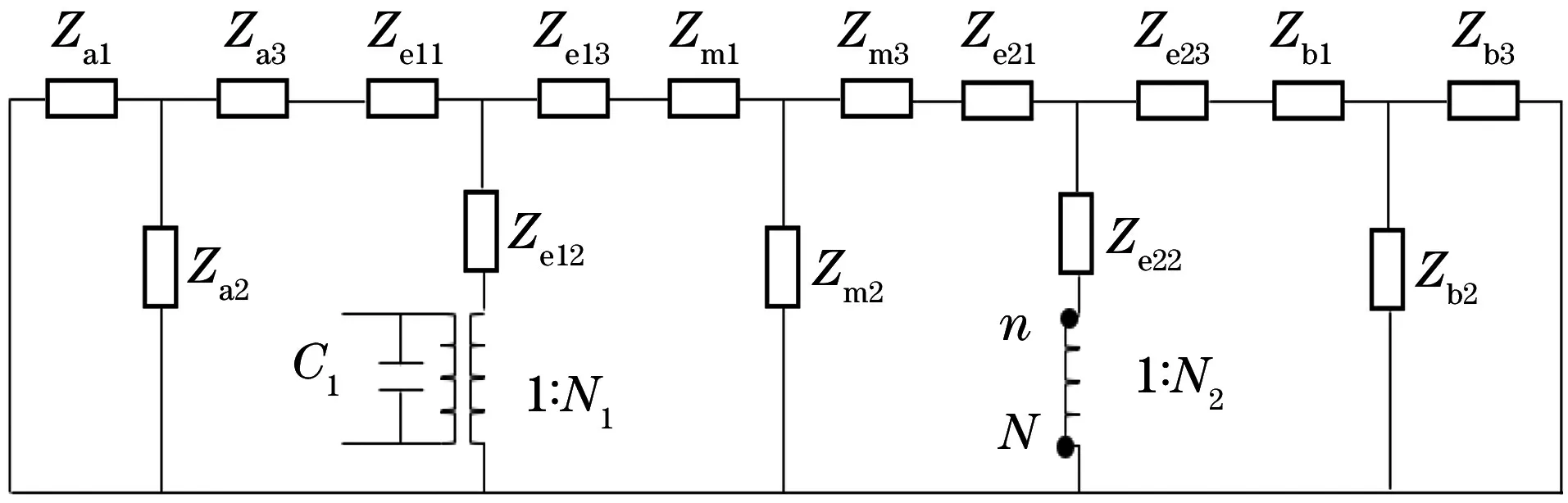
图4 低频时双激励换能器的机电等效电路
Ze-L=0
(8)
工作在高频时,后晶堆近似于短路,其机械端m-M的反射阻抗ZmM=0,则高频时的换能器机电等效电路如图5所示[11]。同样可得到高频后晶堆短路情况下换能器的共振频率方程为
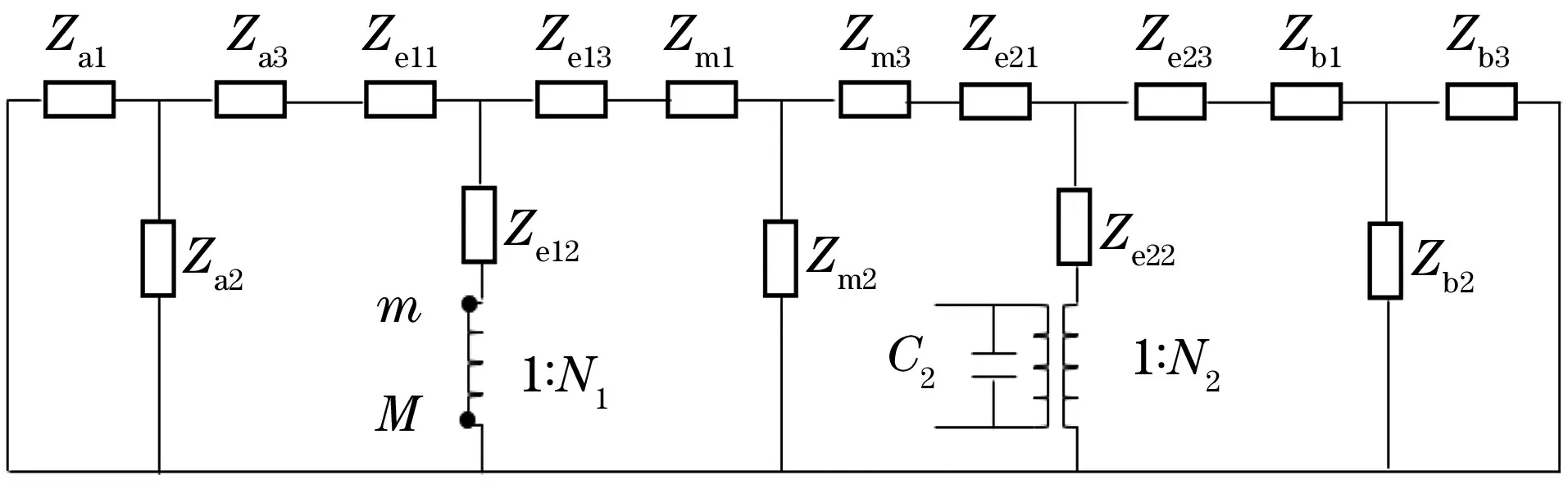
图5 高频时双激励换能器的机电等效电路
Ze-H=0
(9)
纵振换能器在振动时其中间存在振动位移为0的截面,称为节面。对于双激励纵振换能器,其在一阶谐振频率(低频)下振动时,有一个节面,在二阶谐振频率(高频)下振动时,有两个节面。为了简化计算过程,在进行双激励换能器设计时,假定双激励换能器的两个节面分别位于前、后晶堆的前、中、后3个位置,根据节面位置可将换能器分为3部分(A,B,C),节面位置如图6所示。

图6 节面位置示意
A,C部分的机电等效电路如图7所示(图中Zm为前后盖板的等效阻抗;Zpe1,Zpe2,Zpe3为等效阻抗;C0为截止电容;N0为机电转换效率)。由图7可得到低频时,A部分的共振频率方程为

图7 A,C部分的机电等效电路
ZA-L=0
(10)
高频时,C部分的共振频率方程为
ZC-H=0
(11)
在目标频率已知、换能器结构尺寸未知的情况下,Ze-L,Ze-H是La,Lm及Lb的函数;ZA-L是La的函数,ZC-H是Lb的函数。
根据以上分析,对于所研究的双激励纵振换能器,其设计步骤如下所述。
(1) 将目标频率f1,f2分别代入式(10),(11)可求得La,Lb。
(2) 将求得的La,Lb以及目标频率f1,f2代入式(8),(9),分别求得2个中间质量块的长度Lm1,Lm2。二者很可能不相同,当差距较大时,需重新选定节面组合,重复上述步骤,直至Lm1与Lm2的值接近。
(3) 将求得的La,Lb,Lm代入共振频率方程,求得该设计尺寸下双激励换能器的谐振频率,并与预设的目标频率做对比,以验证设计的准确性。
2 双激励纵振换能器仿真设计
基于上述换能器设计理论,首先利用共振频率方程计算得到23,42 kHz目标频率下换能器前、后盖板及中间质量块的长度,然后借助有限元建模将螺栓考虑在内,对换能器结构进行优化设计,并分别计算其在空气、水中的模态及频率响应。设计的双激励纵振换能器的压电材料采用PZT-4压电陶瓷,后盖板、中间质量块材料为45钢,前盖板材料为喇叭状硬铝。
2.1 理论计算
将换能器节点位置均预设于两组压电晶堆前部。利用共振频率方程求得前盖板长度Lb、后盖板长度La以及中间质量块长度Lm1,Lm2,计算得到换能器前盖板理论长度为25.6 mm;中间质量块理论长度为16.3,15.9 mm;后盖板理论长度为26.4 mm。
可以看出,通过高、低频共振频率方程求得的中间质量块长度Lm1≠Lm2,但两者相差较小(相差0.4 mm)。为进一步验证计算结果的准确性,分别计算空气中Lm=16.3 mm和Lm=15.9 mm时的换能器理论导纳曲线,计算结果如图8所示。

图8 空气中双激励换能器导纳曲线的理论计算结果
从图8可以看出,当Lm=15.9 mm时,计算得到的换能器理论谐振频率为23.065,42.035 kHz;当Lm=16.3 mm时,理论谐振频率为22.995,41.825 kHz。两者计算结果接近,且与预设目标频率23,42 kHz相吻合。由于Lm=15.9 mm时,其计算结果与目标频率更为接近,所以初步确定换能器中间质量块的长度为15.9 mm。
为进一步验证理论计算结果的准确性,利用有限元软件对上述设计的换能器进行建模仿真,由于其具有轴对称性,为简化模型,建立了二维对称模型进行计算,其导纳计算结果如图9所示。图9中前两阶频率分别为23.233,39.273 kHz,与理论计算相比,一阶谐振频率的误差为0.168 kHz,二阶谐振频率误差为2.762 kHz,误差产生的原因在于:① 理论计算参数与有限元材料参数存在误差;② 理论计算过程忽略了换能器的机械损耗、介电损耗以及其他损耗的影响。

图9 空气中双激励换能器导纳曲线的模拟计算结果
双激励换能器在2个谐振频率下的振动模态如图10所示。从图10可以看出:换能器在23.233 kHz谐振频率下,只有一个节点,位移最大值在换能器两端且振动相位相反,此时换能器为纵向振动模式;在39.273 kHz谐振频率下,换能器有两个振动节点(位于前、后盖板与晶堆的接触面上),此时换能器为二阶纵向振动模式。
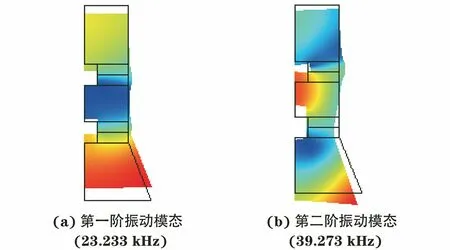
图10 双激励换能器在2个谐振频率下的振动模态
2.2 有限元模拟优化设计
在实际换能器制作过程中,需要预应力螺栓施加预应力,在上节的有限元建模中未考虑螺栓。此外,相比于目标频率42 kHz,上节设计换能器的二阶谐振频率较低,且其对应的导纳过低,这会导致换能器在水中的发射电压响应起伏过大,因此本节将预应力螺栓纳入模型中,并对双激励换能器的结构尺寸进行调整,使其谐振频率更接近目标频率,且在目标频率内,在水中的发射电压响应起伏较小。
基于上节理论计算得到的双激励换能器设计参数,利用有限元软件对换能器设计进行优化,优化后的换能器前盖板长度为32 mm,中间质量块长度为8 mm,后盖板长度为30 mm。
优化后的双激励换能器,除前、中、后质量块长度发生变化外,喇叭状前盖板的辐射面直径也进行了调整,且考虑到制备换能器过程中,压电晶堆与前盖板的对中问题,在前盖板上设计了一定厚度的台阶,优化后的双激励纵振换能器二维模型如图11所示。

图11 优化后的双激励纵振换能器二维模型
对优化设计后的双激励换能器在空气中的振动模态进行仿真模拟,模拟计算结果如图12所示。从图12可以看出,其在空气中的前两阶谐振频率为22.56,41.56 kHz,与预设目标频率接近,对应的导纳为53.4,22.7 mS。
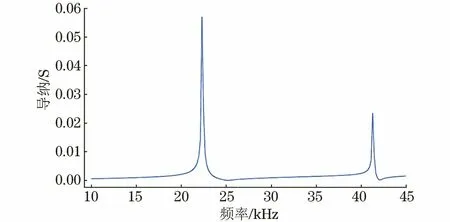
图12 优化后双激励纵振换能器在空气中的导纳曲线模拟计算结果
同时,利用有限元软件对优化后双激励换能器在水中的导纳曲线、发射电压响应曲线进行模拟计算,结果如图13,14所示。由图13可知,该换能器在水中工作时,导纳存在两个谐振峰,分别为22.261,40.754 kHz。相较于空气,水中的谐振频率有所下降,这是因为水的声阻抗大于空气的,所以前盖板的等效阻抗增大,前后盖板的振速比减小,从而使得换能器在水中的谐振频率向低频移动。从换能器发射电压响应曲线可以看出,频率为19.5 kHz~43.2 kHz时,最大发射电压响应为147.1 dB,最小发射电压响应为140.4 dB,起伏为6.7 dB,带宽为23.7 kHz。

图13 优化后双激励纵振换能器在水中的导纳曲线模拟计算结果
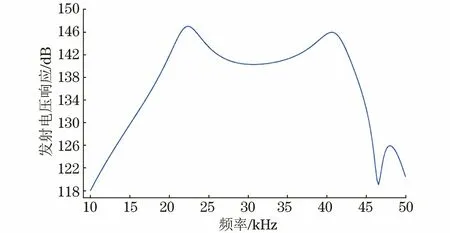
图14 优化后双激励纵振换能器在水中的发射电压响应曲线
3 换能器性能测试
根据理论计算及优化设计的结果,制作了双激励纵振换能器样机,其实物如图15所示。

图15 双激励纵振换能器实物
使用阻抗分析仪对制作的双激励换能器输入导纳进行测试,得到换能器在空气中的输入导纳实测曲线(见图16)。从图16可以看出,制作的换能器实测频率为22.14,41.2 kHz,对应的导纳为47.4,17.7 mS,实测与仿真结果的谐振频率对比如表1所示。从表1可以看出,制作的双激励换能器在空气中实测的谐振频率及其对应的导纳较仿真结果略低,主要原因为仿真时未考虑环氧树脂、电极片的影响,且实际结构的材料参数与仿真的有区别,但实测与仿真的结果相差不大,仿真结果可以为实际制作换能器提供理论依据。
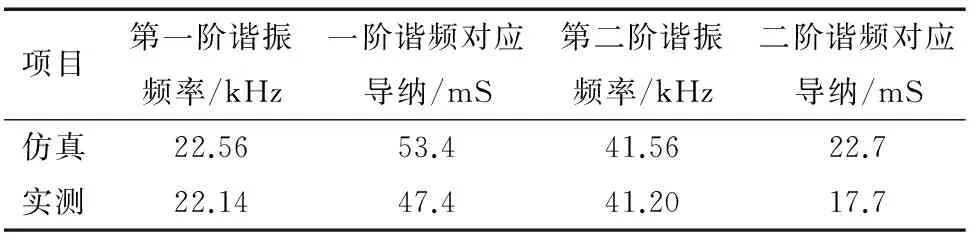
表1 空气中双激励纵振换能器实测与仿真的谐振频率
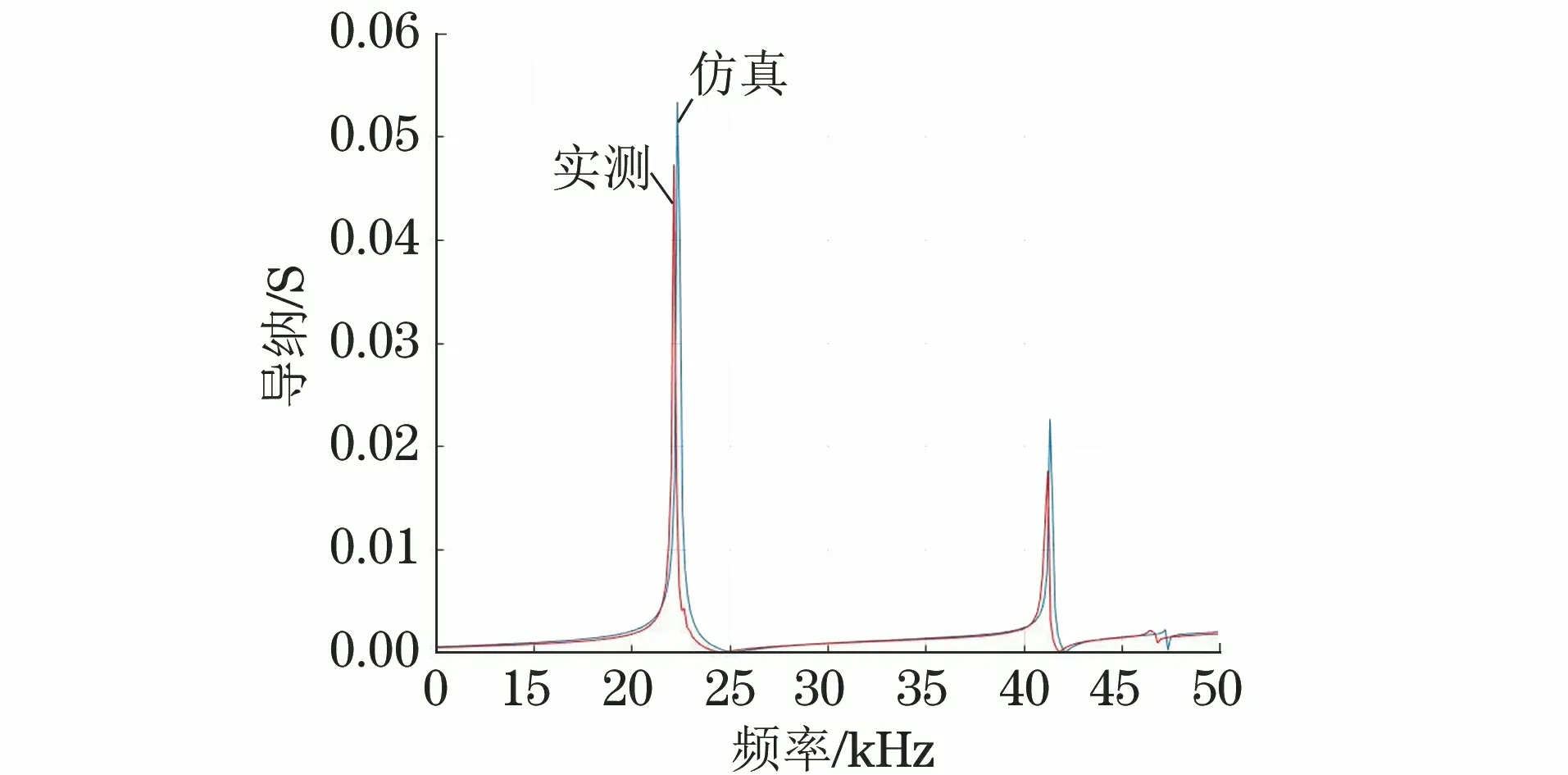
图16 空气中双激励纵振换能器导纳曲线的实测与仿真结果
利用水中测量系统对制作的换能器的水下发射电压响应进行了测试,结果如图17所示。从图17可以看出,在19 kHz43.5 kHz频带内,发射电压响应起伏为8 dB,发射电压响应为137145 dB,相较于仿真结果,实测的响应值整体有所降低,起伏增加了1 dB。
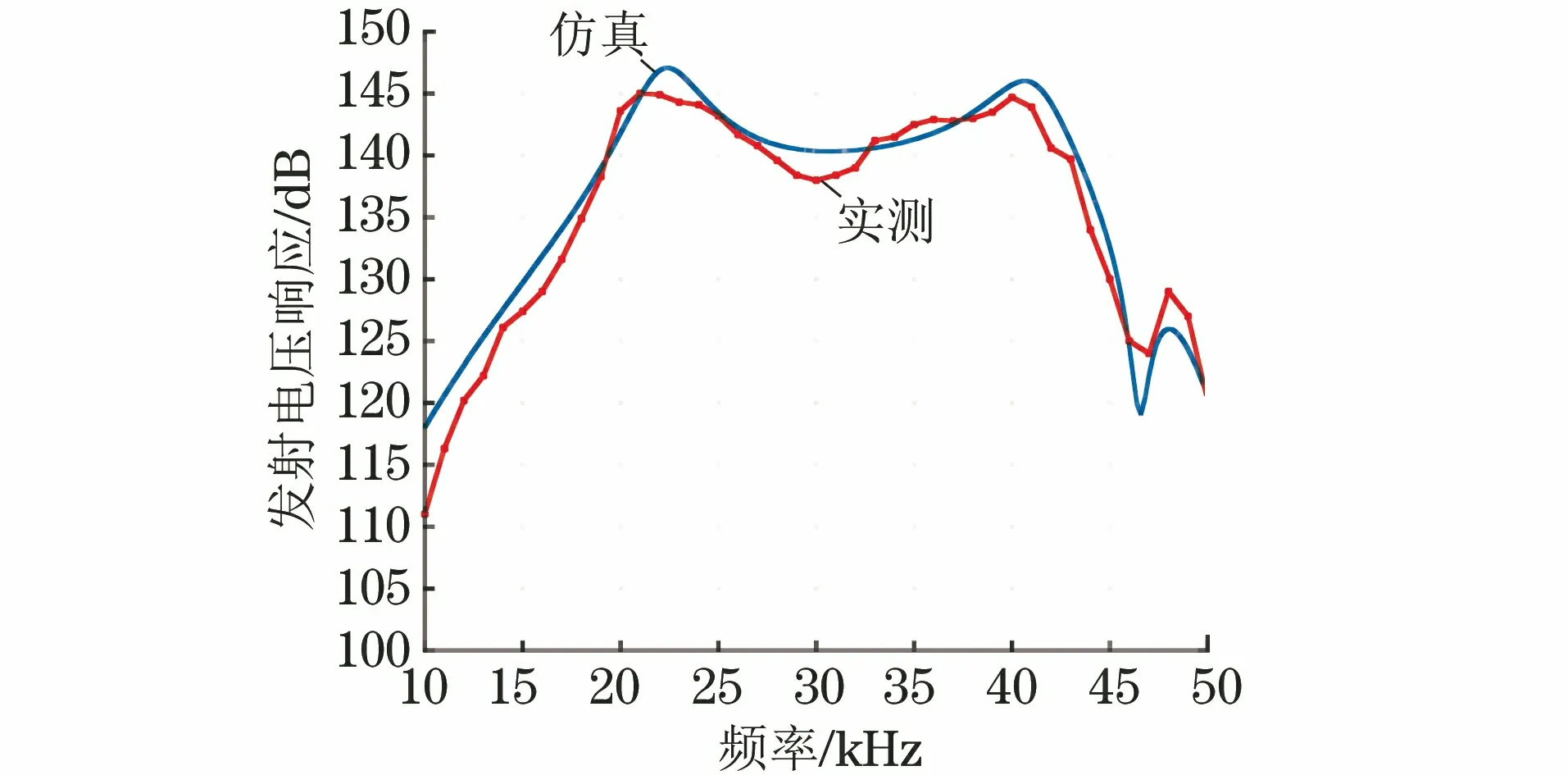
图17 双激励纵振换能器水中发射电压响应的实测与仿真结果
4 结语
首先基于双激励换能器的共振频率方程初步确定换能器尺寸,并通过有限元软件验证了理论计算的正确性。同时在理论设计的基础上,利用有限元软件对换能器进行优化设计,并分别计算了其在空气、水中的导纳曲线和发射电压响应。在此基础上制作了双激励纵振换能器,并对其性能进行测试,实测结果与仿真结果基本吻合。这表明了双激励纵振换能器理论设计方法可以为实际换能器的制作提供依据,为进一步研制双激励纵振换能器奠定了基础。

