二阶离散Holling-Ⅳ型差分系统稳定性分析

李 峥，柏思宇，王 悦，曹名圆

(北华大学数学与统计学院，吉林 吉林 132013)

在捕食者-食饵系统中，功能反应函数起着重要作用[1]，其中Holling-Ⅰ～Ⅲ型功能反应函数在第一象限单调非减，而Holling-Ⅳ型功能反应函数[2]用来描述当食饵密度达到较高水平时，捕食者生长可能受到抑制的非单调反应.随着生物系统的不断发展，学者们利用离散变量对Holling-Ⅳ型差分系统的性质进行了研究[3-8].

如Cinar[3]研究了如下差分系统的正解

Clark和Kulenovi[4，5]研究了如下差分系统的性质

基于离散动力系统的初步研究，本文研究Holling-Ⅳ型差分系统

(1)

正解的渐近性，其中参数α1、β1、γ1、α2、β2、γ2及初始条件u-1、u0、v-1、v0均为正数.本文考虑un和vn的两种不同取法，即un=xn，vn=yn与un=yn，vn=xn.针对这两个差分系统，分别研究它们的平衡点及其稳定性.

1 稳定性分析

首先考虑取un=xn，vn=yn时，系统(1)的稳定性，即

(2)

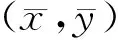
为了构造系统(2)对应的线性化形式，作如下变换

(xn，xn-1，yn，yn-1)→(f，f1，g，g1)

(3)

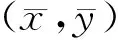
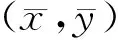
(4)

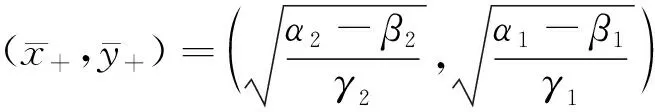
其特征多项式

(5)

定理2如果α1<β1，α2<β2，则系统(2)的平衡点(0，0)局部渐近稳定.

证明：由式(4)易知，系统(2)在点(0，0)处的雅可比矩阵为

其特征多项式

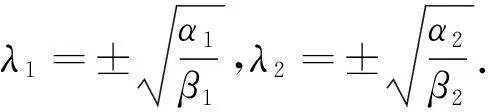
定理3系统(2)的平衡点(0，0)全局渐近稳定.

证明：在定理2结论的基础上，如果平衡点(0，0)是全局吸引子，那么(0，0)是全局渐近稳定的.因此，我们只需证明(0，0)是全局吸引子.

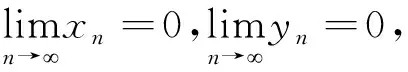
现在考虑第2种取法系统(1)的稳定性，即取un=yn，vn=xn，则有

(6)

与第1种证法类似，作如下变换

(xn，xn-1，yn，yn-1)→(f，f1，g，g1)

(7)

这里f=xn+1，f1=xn，g=yn+1，g1=yn.系统(6)有唯一的平衡点(0，0).基于变换(7)，在点(0，0)处的雅可比矩阵为

(8)

定理4如果α3<β3，α4<β4，则系统(6)的唯一平衡点(0，0)全局渐近稳定.

然后证明(0，0)是一个全局吸引子.因为对系统(6)有

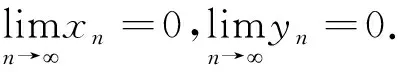
2 数值算例

为了验证我们的结果，本节考虑简单的数值模拟.

例1选取系统(2)初始条件x-1=0.8，x0=3.5，y-1=1.7，y0=1.1，参数α1=118，β1=125，γ1=10，α2=135，β2=140，γ2=12，则系统(2)变为

此时，该系统的仿真结果见图1.

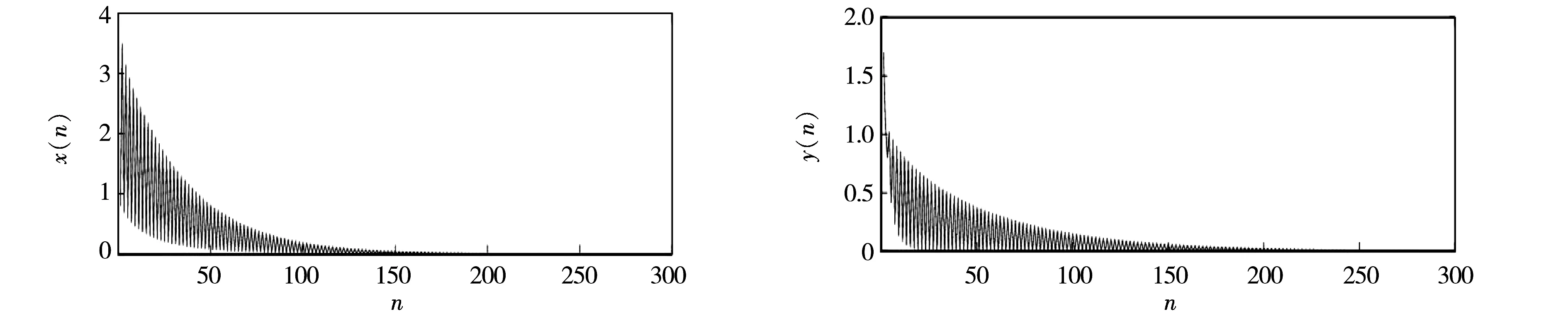
图1 参数α1=118，β1=125，γ1=10，α2=135，β2=140，γ2=12时，系统(2)中xn，yn的时序Fig.1 Plot of solutions xn，ynto Eq.(2) with parameters α1=118，β1=125，γ1=10，α2=135，β2=140，γ2=12

例2选取系统(6)初始条件x1=0.7，x0=1.8，y1=2，y0=1.1，参数α3=150，β3=151，γ3=2.3，α4=165，β4=175，γ4=8，则系统(6)变为

此时，该系统的仿真结果见图2.

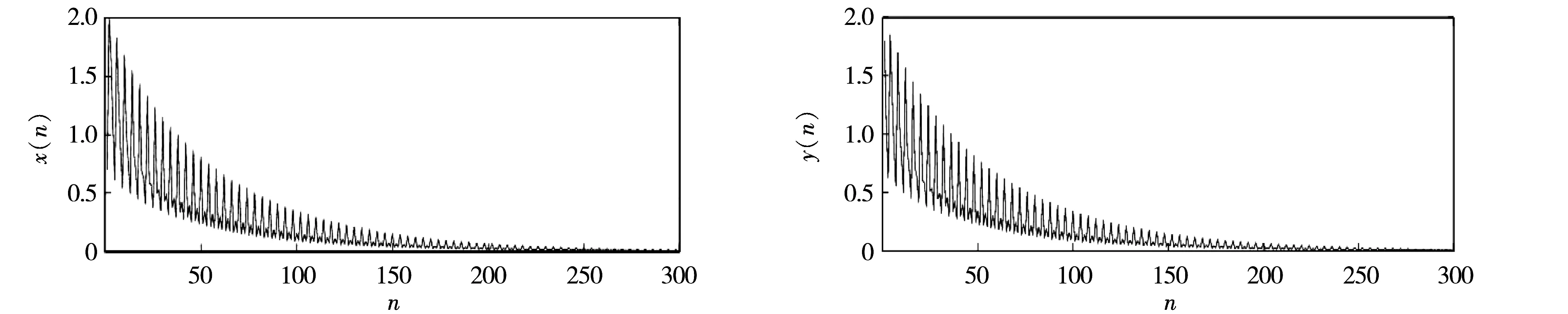
图2 参数α3=150，β3=151，γ3=2.3，α4=165，β4=175，γ4=8时，系统(7)中xn，yn的时序Fig.2 Plot of solutions xn，yn to Eq.(7) with parameters α3=150，β3=151，γ3=2.3，α4=165，β4=175，γ4=8

由图1和图2可见：在两组参数条件下，系统(2)和(6)的解都趋向于平衡点(0，0).这说明系统(2)和(6)的参数只要分别满足条件α1<β1，α2<β2和α3<β3，α4<β4，则平衡点(0，0)均全局渐近稳定.