基于粗糙集理论的信息熵组合权重评价方法

路云龙，李文钰，徐加阳，马 铭

(1.北华大学数学与统计学院，吉林 吉林 132013；2.长春市新凯旋科技有限公司，吉林 长春 130012；3.北华大学大数据与智慧校园管理中心，吉林 吉林 132013)

教学质量评价是高等学校教学管理中的重要环节.在评价数据爆发式增长的环境下，客观、公正、科学地对高校教师教学质量进行综合评价，深入挖掘和研究评价数据背后隐藏的有价值信息，是实现教育数据服务教学的重要课题.高校教师教学质量评价是高校教学质量评价的重要组成部分，评价方法较多，如层次分析评价法、模糊评价法、简单加权法、投入产出评价法等[1].围绕教师评价指标体系权重计算，出现了各种不同的评价模式与方法，但归根结底可以分为3类：主观赋权法、客观赋权法及主客观结合的综合赋权法[2].随着人工智能的不断发展，涌现出了神经网络、遗传算法等智能评价方法[3-6]；文献[7-8]介绍了几种利用数据挖掘方法分析教学相关数据的原理和思路.但借助粗糙集理论挖掘原始定性评价数据，重构评价指标体系，利用不同类型评价方法优势构建新评价方法的研究还不多见.本文利用粗糙集理论对原教师教学评价指标体系进行属性约简，获得优化后的评价指标体系；利用评价数据所包含的信息，结合熵权法确定约简后的评价指标客观权重，利用改进的层次分析法确定评价指标的主观权重，从而获得组合权重；以13名一线教师为例，对比教务系统原有算法，以及学院的教师评价排名，验证本文方法的有效性.

1 相关算法

1.1 自适应遗传的粗糙集约简算法

粗糙集属性约简的目的是利用粗糙集理论约简评教数据中的评价指标集合，删除冗余评价指标，形成一个新的最小约简评价指标集合，优化教师教学质量评价指标.具体是以属性核为起点，以信息熵或者其他准则来评估指标属性的重要度，利用启发式方法逐步向集合中添加核外重要性最高的属性，最后得到最小约简.本文采用基于自适应遗传算法的粗糙集约简算法对教学评价指标属性集合进行约简[9].该算法从属性核出发，按照一定规则操作(选择、交叉、变异等)，使得对应于属性核中的个体基因在整个遗传过程中都会受到保护.

算法1：基于遗传算法的粗糙集约简算法

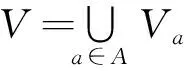
输出：最小约简集合c∈C.

1)计算决策属性D对于条件属性C的依赖度.

2)计算每个c∈C对D的重要性，计算条件属性核，如果条件属性核的依赖度等于1)中计算的依赖度，算法终止；否则转3).

3)按照2)计算的属性核，初始化种群.

4)计算种群中单独个体的适应度值，进行遗传算子操作(选择、交叉、变异).

5)判断若干代个体适应度值是否不再提高，如果不再提高算法终止；否则转4).

1.2 评价指标权重算法

对于经算法1属性约简后的评价指标体系，利用熵权法确定约简后评价指标的客观权重，再利用改进的三标度层次分析法确定主观权重，将二者加权做和获得评价指标的组合权重，进而建立评价模型.

1.2.1 互信息的客观权重法

在信息论中，熵是对不确定性信息的一种度量，通过计算指标的信息熵来判断其相对变化程度 (离散程度).指标的相对变化程度越大，其信息的效用价值就越大，该指标在综合评价中对系统整体的影响也就越大，则对该指标赋予较大的权重.因此，我们可以把它作为一种对评价指标客观赋权的方法.

对于知识表达系统S，考虑到决策属性对条件属性的依赖性，引入互信息，建立客观权重算法.下面给出相关理论[10]：

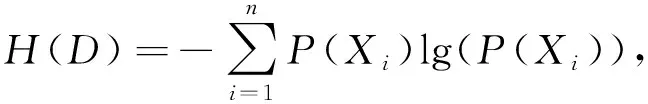
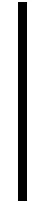
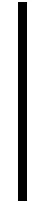
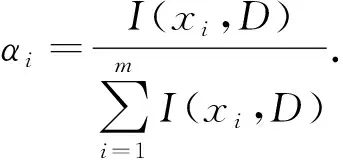
算法2：粗糙集互信息的客观权重法

1)根据学生评教数据随机抽取建立信息系统S.

2)初始化信息系统S，若被评价对象U中出现相同评价结果，则需保留1个.

3)根据信息熵概念，进一步简化信息系统，计算每个属性x和决策D的互信息I(xi，D)，i=1，2，…，m的值，计算方法见定义4.

4)计算各评价指标的客观权重αi，i=1，2，…，m，见定义5，其值越大表示该评价指标在评价体系中的重要性越大，对教学水平的影响也越大.

1.2.2 层次分析的主观权重法

层次分析法(Analytic Hierarchy Process)是一种定性和定量相结合的，系统化、层次化的决策方法.由于传统的层次分析法存在判断矩阵不易构造且一致性差等问题，需要多次构造判断矩阵并检验一致性，增加了计算代价.文献[11]提出了三标度法，该方法易于构造判断矩阵，但计算精度低于传统的1-9标度法；文献[12]提出指数标度法，该方法计算精确，获得的判断矩阵的一致性优于传统的1-9标度法，但判断矩阵构造困难；文献[13]提出指数(0，2)标度AHP法，该方法具有判断矩阵易构造、计算精度高等优点.

本文对文献[13]中的方法给予如下3方面改进，使得改进后的方法更加适用于研究实际问题.

ⅰ) 将(0，2)互补性三标度法改成(-1，1)互反性标度法.因为指数标度法是用互反性标度来构造的，所以这样做能够提高两种方法的契合度，已有实例也验证了这一点.

ⅱ)求解判断矩阵算法的改进.文献[13]计算判断矩阵的运算规则忽略了三标度法能够转换成其他标度法这一特性，而本文在原算法基础上，结合指数标度法，设计了新规则来计算判断矩阵，使得改进后的算法既符合指数标度的计算要求，又保留了三标度法算法的优越性.

ⅲ)改用特征向量法计算权向量.文献[14]论证了在指数标度中利用特征向量法确定权向量要优于根法.

算法3：改进的三标度层次分析法

1)设同一层次中的n个元素，对上一层中某一元素进行两两比较，依三标度法可得如下比较矩阵A：

各标度值含义见表1.

表1 标度值含义Tab.1 Scale meanings

2)计算各元素的重要性排序指数ri：

若用Amax表示最大排序指数对应的元素，Amin表示最小排序指数对应的元素，bm表示Amax与Amin比较时按九标度法给出的重要程度，则判断矩阵B中元素为

(1)

3)基于判断矩阵B构造指数判断矩阵C：

其中：a为大于1的实参数.决策者可通过调整a值获得满意的排序权值.

4)利用特征向量法计算主观权重βi，并进行一致性检验.通过算法2和算法3计算主客观权重，进而计算组合权重，获得评价指标的最终权重.

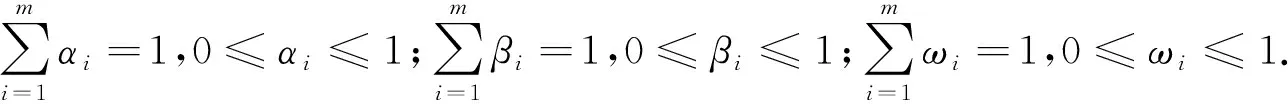
ωi=μαi+(1-μ)βi，i=1，2，…，m

(2)

这里，μ表示决策者偏好的主观或客观程度.

2 模型构建

将上节介绍的3种算法相结合，建立一种新的教学质量评价模型，见图1.

图1 评价模型Fig.1 The evaluation model

2.1 基于粗糙集约简算法的教师教学评价指标体系

构建合理的评价指标体系是评价的核心环节.表2为某高校教师教学质量评价指标体系.每名同学通过教学管理系统的10个指标对教师教学质量进行评价，评价分为好、较好、一般3个等级，量化标准见表3.

表2 某高校现行教学质量评价指标体系Tab.2 The current teaching quality evaluation index system of some university

表3 单指标数据处理准则Tab.3 Data processing rules of single index

利用学生评教数据集并结合算法1对上述10个指标进行属性约简.随机抽取13 位教师的原始评价数据，建立知识表达系统S，见表4，其中，条件属性值为{好，较好，一般}，决策属性值为{好，较好，一般，较差，差}.根据粗糙集约简理论，由于u7、u9、u10、u12、u13这5位教师的评价指标下的取值完全相同(所在的行)，因此，只需保留u7.

表4 决策Tab.4 Decision

调用基于算法1编制的 ROSETTA软件[15]，通过分析提取规则，并咨询专家意见，从29条约简结果中选择评价指标体系为

{C1，C3，C5，C7}.

2.2 教学评价体系指标权重的确立

前面已经获得约简后的教学质量评价指标体系，接下来要确定指标的权重，进而建立评价模型.

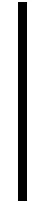
依据定义5，计算客观权重：

α1=0.210，α3=0.239，α5=0.321，α7=0.230

(3)

利用算法3，计算主观权重.

1)由三标度法建立比较矩阵A：

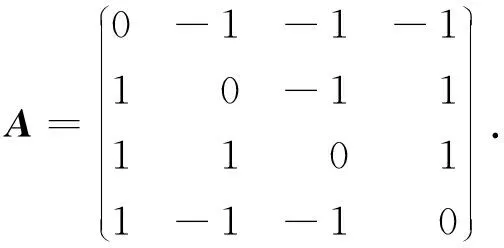
2)计算各元素的重要性排序指数ri，并由式(1)得到判断矩阵B，其中，bm的值按照1-9标度给出，bm=5：

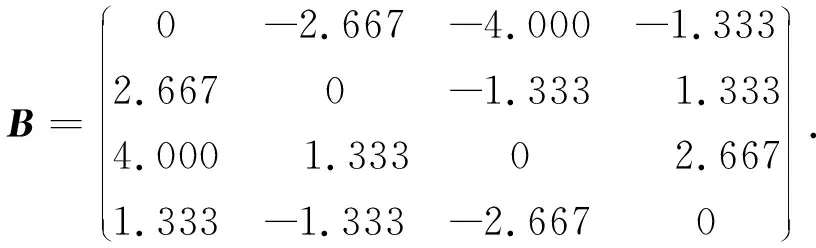
3)基于判断矩阵B构造指数判断矩阵C，取a=1.316[16]：

利用特征向量法计算主观权重并通过一致性检验，求得主观权重

β1=0.133，β3=0.276，β5=0.399，β7=0.192

(4)

由式(2)、(3)、(4)可得组合权重ω1=0.172，ω3=0.257，ω5=0.360，ω7=0.211，这里取μ=0.5.

3 教学评价结果分析

将利用本文算法计算的13名教师教学评价综合评分及排名与教务系统、学院中教师的教学评价结果进行比较.

依据约简后的学生评价指标体系(C1、C3、C5、C7)及组合权重，利用

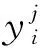
表5 总评分Tab.5 Total score

3.1 评价分数对比

由图2发现：综合评分曲线位于教务处评分和学院评分曲线之间，说明该方法既能考虑学生评分又能兼顾学院专家评分，得到综合的评价结果，该评价结果可为教学管理部门制定合理的指标权重提供重要依据.

3.2 评价排名对比

由图3可见：折线前、后部分综合评分排名与学生评分排名的折线完全重合，说明本文所提方法能够非常准确地捕捉到排名靠前和靠后的教师，与学生评价的结果基本相符；学院专家评分折线整体波动较大，与学生评分折线有很大出入；综合评分折线上仅编号3和12的教师排名有明显变化，但变化不太大.分析了解教师实际课堂授课情况，以及学生对排名中间的教师可能出现不够认真负责的态度认为，本文的评价结果更加符合实际情况，建议学院采取更为合理的教师教学质量评价方法.

图2评分对比Fig.2Comparison of scores图3排名对比Fig.3Comparison of ranking

4 结论与讨论

本文提出了基于粗糙集理论的信息熵组合权重评价方法.结合一线教师和教学管理部门的意见，利用基于遗传算法中的粗糙集算法对教务系统中使用的评价指标体系进行约简，获得新的评价指标体系；结合信息熵法和层次分析法获得评价指标体系的组合权重；对某学院13名一线教师进行测算，并同教务系统的评价结果及学院评价结果进行比较.结果表明，所提算法能够优化评价指标体系，更好地反映教师的教学情况，同时可为教学管理部门进行教学管理及规划提供参考.本文将粗糙集理论作为一种数据挖掘技术应用于教师教学质量评价还有许多方面需要完善，例如，属性约简的计算方法及择优，以及同其他评价方法集成等都是值得关注的方向.