基于差别矩阵的区间值决策系统β分布约简
李磊涛,张 楠*,童向荣,岳晓冬
(1.数据科学与智能技术山东省高校重点实验室(烟台大学),山东烟台 264005;2.烟台大学计算机与控制工程学院,山东烟台 264005;3.上海大学计算机工程与科学学院,上海 200444)
0 引言
粗糙集理论[1-5]是一个重要的数据处理工具,可以用来处理数据中的不确定性问题,最先由Pawlak[1]提出,已应用于许多领域。属性约简[1-7]是粗糙集理论的核心研究内容之一。当前,消除不必要的属性、缩小数据规模从而加速数据的处理显得尤为重要,而属性约简的目的就是尽可能消除数据中不必要的属性,得到决策系统中某种分类特征不变的最小属性子集。通过属性约简既可以缩小数据规模又不会破坏知识的原始信息,恰好满足了当前的需求。目前已经有许多学者对知识约简做了大量工作。1992年,Skowron 等[8]提出了一种基于差别矩阵的正域约简方法,随后国内外许多学者对此做了大量的扩展工作;1999年,苗夺谦等[9]提出了在决策信息表中属性重要性度量的概念;2003 年,张文修等[10]提出了最大分布属性约简以及分配属性约简的算法;2007 年,徐伟华等[11]在不协调信息系统中提出了基于优势关系的经典分布和最大分布约简的概念,并建立了相应的差别矩阵;2017年,Su等[12]提出了一种基于组合子集的编码方法,并给出了一种基于粗糙集理论和鱼群算法的最小化属性约简的搜索策略;2018年,Liu 等[13]在决策系统中提出了特定类β分布保持约简的概念;2020年,Abdolrazzagh-Nezhad 等[14]通过构造一个新的成本函数并利用改进的文化算法来解决多目标属性约简问题,最后提出了无监督属性约简的新方法。
以上传统的粗糙集理论都是处理单一值数据,并不适合于处理区间值数据。实际应用中存在许多区间值形式的数据,它们通过不精确的估计数值范围来描述对象,因此在粗糙集领域中,区间值信息系统受到广泛研究。2008 年,Leung等[15]考虑到两个区间值数据的相似度问题提出了误分率的概念,揭示了在两个区间值数据的交集部分被错误分类为另一个区间值的程度;2009 年,张楠等[2]提出了极大相容块的概念,去除了相容类中不满足传递性的对象,提高了分类精度,并在区间值信息系统中构造了对于任意对象的新的粗糙近似;2011 年,Dai 等[16]基于相容关系提出了扩展条件熵和粗糙决策熵以及区间近似粗糙度的概念,实验结果表明粗糙决策熵的度量要优于区间近似粗糙度;2014年,徐菲菲等[7]提出了基于属性的依赖度以及互信息的区间值启发式属性约简,选择属性依赖度高、互信息低的属性加入约简集合;2015 年,Yang等[17]提出了一种基于α参数优势的粗糙集方法处理区间值信息系统问题,并为了简化决策规则而引入了上下近似约简;2016 年,张楠等[18]在区间值决策系统中基于正域的确定性以及边界域的不确定性提出了确定性规则和不确定性规则保持约简;2018 年,尹继亮等[19]基于区间值决策系统提出了最大分布约简的概念,只将最大的分布值进行处理,实验结果表明该算法的效率高于经典的分布约简;2020 年,Liu 等[20]在区间值信息系统中提出了一种无监督属性约简方法,利用模糊类构造α-近似等价关系以及近似等价类,从而提出了新的属性重要性的度量方式。基于以上研究可知,文献[7]提出了依赖度以及互信息的约简目标,文献[16-20]则提出了决策熵、条件熵、确定性、不确定性以及最大分布的约简目标。
目前,未有对区间值决策系统下β分布约简的讨论,最大分布约简虽然提高了效率,但只考虑了最大的分布,所以会损失一些信息,因此本文提出了在区间值决策系统下β分布约简的概念,可以有效处理区间类型的数据。该方法通过放松构造差别矩阵的条件减少差别矩阵的元素,可以保留分布信息并减小约简长度。
1 基本知识
1.1 区间值决策系统
在应用中存在大量的区间值数据,它规定了某个属性的取值范围,接下来给出相关概念。


1.2 相似度
相似度表示两个区间值数据之间相似的程度,通过相似度可以求出区间值系统的相容关系及相容类,接下来给出相关定义。

对于区间值决策系统IdS=(U,C∪D,V,f),U为包含n个对象的论域,则在相似度阈值θ下相容类集合定义如下:

在单值决策系统中应用经典粗糙集理论时,对象之间的等价关系具有自反性、对称性、传递性,由此获得的等价类实现了对于论域U的划分,而区间值决策系统中的相容类实现了对于论域U的覆盖。
例1 对于给定的区间值决策系统,如表1所示,论域U={x1,x2,…,x6}为对象的集合,C={a1,a2,a3,a4}为条件属性的集合,决策属性D={d}。

表1 区间值决策系统Tab.1 Interval-valued decision system


1.3 区间值决策系统的经典分布约简
文献[22]中提出了区间值决策系统经典分布约简的思想,下面给出其相关定义和经典分布约简算法的描述。
定义6假设IdS=(U,C∪D,V,f)是区间值决策系统,IdS的差别矩阵为n×n的矩阵,记为M=(cij)n×n,其中cij满足:
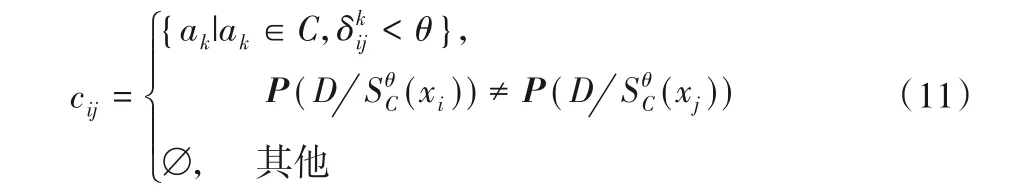
其中:cij为差别矩阵的第i行、第j列元素,i,j=1,2,…,|U|。[22]
定义7设IdS=(U,C∪D,V,f)是区间值决策系统,ak表示条件属性的第k个属性,cij为差别矩阵的第i行、第j列元素,该区间值决策系统对应的θ-相容类分布约简的差别函数是由与条件属性对应的变元构成,该函数如下:

其中:∨cij=∨ak,ak∈cij表示所有属性对应变元的析取项。通过吸收律和分配律将合取范式Fθ(IdS)转化为析取范式Hθ(IdS)。[22]
定理1设IdS=(U,C∪D,V,f)是区间值决策系统,Hθ(IdS)是分布约简的差别函数Fθ(IdS)的转化,若R是一个分布约简结果,当且仅当R是Hθ(IdS)的一个包含项。[22]
基于差别矩阵的分布约简算法(Distribution Reduction Algorithm based on Discernibility Matrix,DRADM)描述如下。

2 区间值决策系统的β分布约简
本章在区间值决策系统中应用β概率分布,提出了基于差别矩阵的区间值决策系统β分布约简算法。






在步骤6通过差别函数转化求得β分布约简部分:首先计算差别函数的项数,最差情况下整个下三角部分均需计算,因此项数为|U|22;然后计算每两项的转化时间,假设最坏情况下每一项均有最多|C|个元素,因此时间复杂度为O(|C|2),所以总的时间复杂度为

3 实验与结果分析
在本章将基于差别矩阵的区间值决策系统β分布约简算法通过UCI(University of California-Irvine)数据集进行实验验证,具体实验包括:约简结果的对比和算法效率差异的对比。
实验环境为:个人笔记本电脑,Inter Core i5-8300H CPU,主频为2.30 GHz,内存为8 GB,操作系统为64 位Windows 10家庭版,程序运行环境为Python 3.7。
实验选取了14 组UCI 数据集,数据集的相关信息如表2所示(表中|U|为对象数目,|C|为条件属性数目)。对于非数值的类别数据用0,1,2,…数值数据代替,对于缺失值则用该缺失值所在列的最频繁项的值代替,由于这些数据集每一项的值都是单值,因此要把这些数据集转化为区间值数据集,本文采用文献[23]中介绍的转化方法。

表2 UCI数据集Tab.2 UCI datasets

3.1 约简结果对比
本节在表2 所示的14 组UCI 数据集上将本文提出的β-DRIVS 与DRADM[22]以及最大分布约简算法(Maximum Distribution Reduction Algorithm based on Discernibility Matrix,MDRADM)[19]的约简结果和对应的压缩比(压缩比为最小约简长度与属性长度的比值)进行比较。当τ=2,θ=0.4,0.5,0.6,β=0.3,0.5,0.7时进行实验,结果如表3~5所示。为描述方便,表3~5中较长的集合在表6中列出。
从实验结果可以看出,大多情况β分布约简结果中的蕴涵项是DRADM 约简结果的子集,这是因为当β=0.5时,假设数据集的概率分布形如可得:此时经典概率分布与β概率分布所得差别矩阵相同,因此两者约简结果相同。
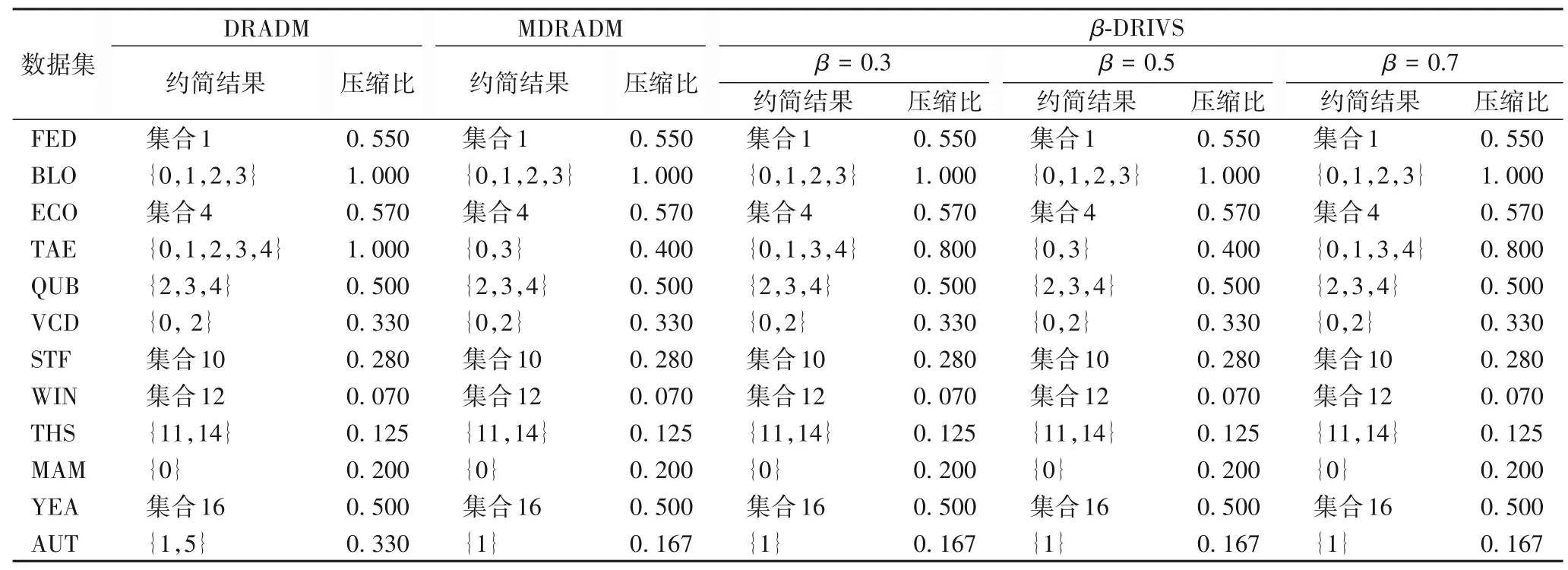
表3 θ=0.4时UCI数据集约简结果对比Tab.3 Comparison of reduction results on UCI datasets when θ=0.4
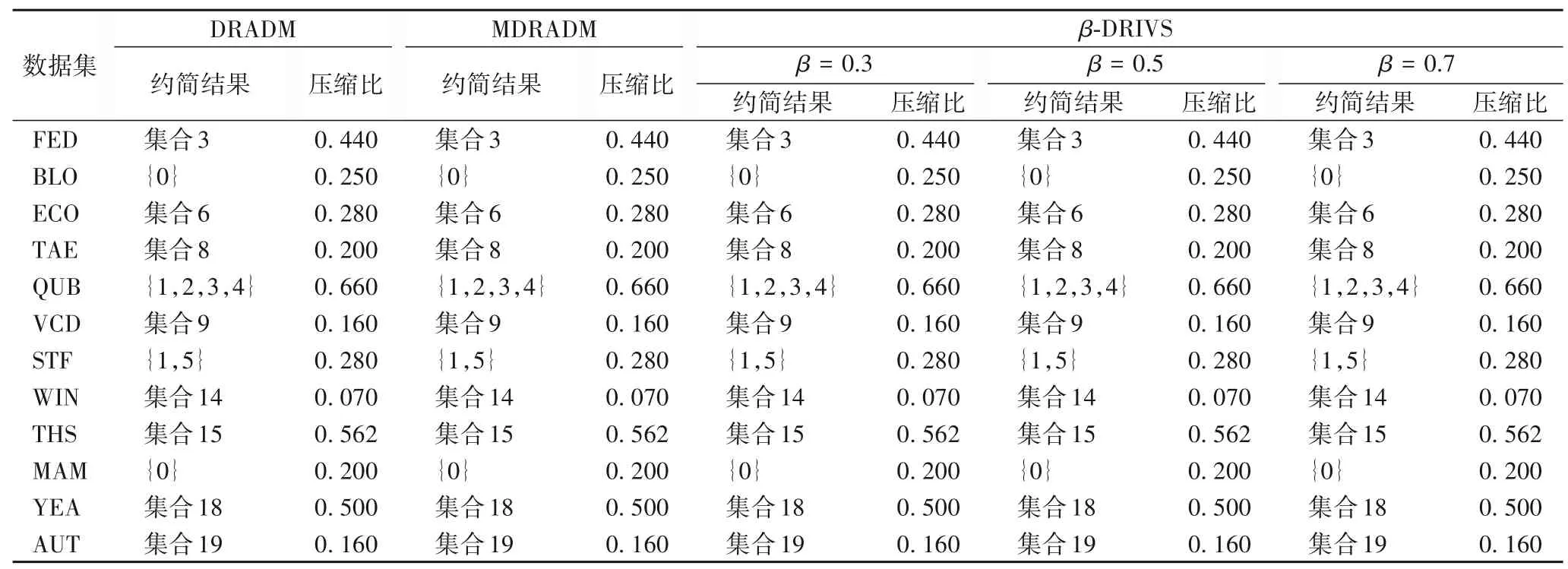
表5 θ=0.6时UCI数据集约简结果对比Tab.5 Comparison of reduction results on UCI datasets when θ=0.6

表6 较长的集合列表Tab.6 Longer collection list
表7~9 分别是当θ=0.4、θ=0.5、θ=0.6,τ取2 时在Statlog 数据集上取不同β值的β-DRIVS 以及DRADM 和MDRADM 在不同对象数目条件下约简结果的对比。表中,约简长度指每个算法的约简集合中最短的约简长度。相应的集合为:集合1={{4,0},{5,0},{14,0},{4,6},{4,8},{4,10},{4,11},{5,6},{5,8},{5,10},{5,11},{14,6},{14,8},{14,11},{14,10,1},{14,10,7},{14,10,13},{14,10,15}};集合2={{0,5},{5,6},{8,5},{10,5},{11,5}};集合3={{5},{14,0},{0,4},{0,9},{0,13},{0,15},{14,1},{14,2},{14,4},{6,4},{8,4},{10,4},{11,4},{14,6},{6,9},{6,13},{6,15},{14,7},{14,8},{8,9},{8,13},{8,15},{14,9},{10,9},{11,9},{14,10},{10,13},{10,15},{14,11},{11,13},{11,15},{14,12},{14,13},{14,15},{0,16,1},{6,16,1},{8,16,1},{10,16,1},{11,16,1}}。
在表9 中,当对象数目分别为100、200、400、600、846 时,β-DRIVS 的平均约简长度分别为1.6、2.2、1.4、2.4、2.6,DRADM 约简长度分别为2.0、3.0、3.0、4.0、4.0,MDRADM 约简长度分别为2.0、3.0、3.0、4.0、3.0,本文提出的算法约简长度最短。从表7~9 可以看出,随着β值的改变,β分布约简的约简结果也发生了变化。当β=0.5 时,假设数据集概率分布形如当β=0.4 时不同β值的算法得到的差别矩阵不同,因此随着β的变化,所得的约简结果也发生变化,此时约简效率也会变化。3.2节将讨论β取值的变化对于约简效率的影响。
3.2 约简效率差异对比
本节在数据集Liver Disorders、BLOGGER、Teaching Assistant Evaluation、Auto Mpg 上,当相似度阈值θ=0.4,0.5,0.6 时,对不同β取值的β-DRIVS 进行约简效率差异对比。由于β=0.3 与β=0.7 的约简结果相同,β=0.1 与β=0.9 的约简结果相同,因此在本节只对β=0.1,0.3,0.5 三种情况下的算法进行约简效率差异对比。
在上述四个数据集上,计算相容类花费了大部分时间,而通过差别函数的转化求得约简时间相对较少,不同β取值只会对差别函数转化的效率产生影响,因此通过曲线无法体现不同β取值对约简效率的影响。本节通过Wilcoxon 秩和检验[24]来展现约简效率差异,通常设置显著性水平为0.05。对于本文算法:假设两个不同β取值的β-DRIVS 约简效率没有明显变化。本实验每次对两组约简效率数据进行检验,每组数据为20 次约简的时间消耗(在20 个数据下,检验结果相对较好)。如果返回的p-value小于0.05,那么假设不成立,即约简效率有明显变化;反之假设成立。
表10 是当θ=0.4、θ=0.5、θ=0.6,τ取2 时,不同β取值的β-DRIVS 在数据集Liver Disorders、BLOGGER、Teaching Assistant Evaluation、Auto Mpg 上p-value的取值,其中下划线标注的是小于0.05的p-value数据。
由表10 可以看出,在数据集Liver Disorders、Teaching Assistant Evaluation、Auto Mpg 上,当相似度阈值θ=0.5,0.6时,以及在数据集BLOGGER 上相似度阈值θ=0.6时,对不同β值下的约简效率进行秩和检验所得的p-value均大于0.05,此时β值对于约简效率几乎没有影响。在这种情况下输出分布结果,发现分布均为(0,1)。此时β值不能使概率分布发生变化,因此不能影响约简效率。

表7 θ=0.4时Statlog数据集约简结果对比Tab.7 Comparison of reduction results on Statlog datasets when θ=0.4

表8 θ=0.5时Statlog数据集约简结果对比Tab.8 Comparison of reduction results on Statlog datasets when θ=0.5

表9 θ=0.6时Statlog数据集约简结果对比Tab.9 Comparison of reduction results on Statlog datasets when θ=0.6

表10 约简效率差异的对比Tab.10 Comparison of reduction efficiency difference

在数据集BLOGGER 上:当θ=0.4 时,根据所得的p-value值,可以看出β取0.1 或0.3 与β取0.5 的约简效率有较大差异,而β取0.1和0.3时约简效率几乎没有差异;当θ=0.5时,β取0.1 或0.5 与β取0.3 的约简效率有较大差异,而β取0.1和0.5时约简效率几乎没有差异,原因是这几种情况下β分布相同。在数据集Teaching Assistant Evaluation 上,根据p-value可知β取0.3 或0.5 与β取0.1 的约简效率有较大差异。β取0.3 和0.5 时约简效率几乎没有差异,原因与BLOGGER 数据集情况类似,此处不再赘述。在数据集Auto Mpg 上,根据pvalue可知三种不同的β取值对于约简效率均有很大影响,原因与Liver Disorders数据集情况相同,此处不再赘述。
4 结语
为了有效处理区间类型数据,本文提出了区间值决策系统β分布约简的概念,构造了对应的差别矩阵和差别函数,提出了基于差别矩阵的区间值决策系统β分布约简算法,并在14 组UCI 数据集上通过与DRADM 和MDRADM 的约简结果对比来验证算法的有效性,而且在不同的β取值下做了约简效率的对比。由于不同的β值会对约简效率产生影响,因此在未来的研究中要选取合适的β值来简化差别矩阵。本文的算法是在一定条件下提出的,因此在更加泛化的关系下获得约简是未来的研究方向之一。

