改进回溯搜索算法解决光伏模型参数识别问题

张伟伟，陶 聪，范 岩，于坤杰，文笑雨，张卫正*

（1.郑州轻工业大学计算机与通信工程学院，郑州 450000；2.郑州大学电气工程学院，郑州 450000）

0 引言

可再生能源的利用是当前研究热点之一。太阳能通过光伏发电系统被转化为电能，是一种非常好的可再生能源。但是，光伏发电系统一般运行在室外环境，其光伏阵列很容易出现故障，这将严重影响太阳能的利用效率。基于实测的电压电流数据建立精确的光伏阵列模型，对光伏系统进行及时的控制和优化是非常重要的。近年来学者们建立了若干数学模型，成功地描述了光伏系统的性能和非线性行为，其中Alam等［1］运用了单二极管模型和双二极管模型来描述光伏系统。此外，光伏模型的准确性主要取决于其模型参数，但是这些参数通常由于老化、故障和不稳定的运行条件不断变化导致可用性下降。因此，准确、可靠地识别模型参数对于光伏模型的评价、优化和控制是十分重要的，这也推动了近年来各种参数识别研究的发展。

光伏模型的参数识别是一个多变量且具有多个局部极值的非线性多模态问题［2-12］，在采用确定性技术进行参数识别时，很容易陷入局部最优［9-11］。启发式方法由于对问题特性没有特别的限制，尤其适合求解各种复杂的“黑箱问题”，因此被广泛应用于光伏模型的参数识别等问题上。

在文献［2］中，提出了一种基于扰动变异分类的粒子群优化（Classified Perturbation Mutation based Particle Swarm Optimization，CPMPSO）算法，并利用阻尼约束处理策略解决陷入局部最优问题。在文献［3］中，通过引入搜索算子，提出了一种扰动随机分形搜索（perturbed Stochastic Fractal Search，pSFS）算法的参数估计方法。在文献［4］中，提出了一种基于生物地理学的异质杜鹃搜索（Biogeography-based Heterogeneous Cuckoo Search，BHCS）算法，该算法将杜鹃搜索（Cuckoo Search，CS）和基于生物地理的优化（Biogeography-Based Optimization，BBO）进行融合，应用于解决不同光伏模型的参数估计问题。在文献［5］中，提出了一种基于自适应教与 学 的 优 化（Self-Adaptive Teaching-Learning-Based Optimization，SATLBO）算法用于光伏模型的参数识别。在文献［6］中，提出一种基于广义对立的教与学优化（Generalized Oppositional Teaching Learning Based Optimization，GOTLBO）算法来识别太阳能电池模型的参数。在文献［7］中，设计了一种简化的基于教与学的优化（Simplified Teaching-Learning-Based Optimization，STLBO）方法，该方法采用精英策略和局部搜索来识别太阳能电池的参数。在文献［8］中，提出一种逻辑混沌JAYA（Logistic Chaotic JAYA，LCJAYA）算法，在LCJAYA 中将logistic 混沌映射策略引入到JAYA 算法的求解更新阶段，提高算法的种群多样性。在文献［9］中，提出一种性能导向的JAYA（Performance-Guided JAYA，PGJAYA）算法来提取不同光伏模型的参数。在文献［10］中，提出了多重学习回溯搜索算法（Multiple Learning Backtracking Search Algorithm，MLBSA）来解决不同光伏模型的参数识别问题。Yu 等［11］提出了一种改进的JAYA（Improved JAYA，IJAYA）优化算法用于解决不同光伏模型的参数识别问题。文献［13］中将广义反向学习与差分进化的改进变异和交叉机制混合到粒子群优化算法中，解决约束优化问题。文献［14］中提出一种基于教与学的优化（Teaching-Learning-Based Optimization，TLBO）算法解决机械设计优化问题。

文献［15］提出的回溯搜索算法（Backtracking Search Algorithm，BSA）具有结构简单、高效、快速的特点，并且对初值不敏感，在选择操作中不依赖“精英选择”策略，从而更适合求解多模态优化问题；另外，BSA 同时使用当前种群和历史种群来更新个体，相较于单一的种群，增加了种群间的信息交流，不仅提高了种群多样性，还增加了引导信息指导当前种群个体进化。鉴于其以上优点，BSA 已经被广泛地用于参数识别［16-17］、流水车间调度［18-19］等。在求解光伏模型参数识别问题时，Yu 等［10］针对BSA 存在收敛速度慢，易陷入局部最优的问题进行改进提出了多重学习回溯搜索算法（MLBSA）。在MLBSA 中，种群个体同时利用当前种群和历史种群进行学习，保持了种群多样性，增加了算法的探索能力。其他个体向当前种群的最优个体进行学习，提高了收敛速度。然而，MLBSA 的全局寻优和局部收敛能力之间的平衡主要靠两个随机数的关系来确定，这将对算法的稳定性带来负面的影响。

针对以上问题，本文提出了改进回溯搜索算法（Modified BSA，MBSA）。本文的主要工作如下：

1）针对BSA 容易陷入局部最优，以及全局寻优与局部收敛能力不均衡的问题，引入了个体适应度量化排队机制；

2）为提升种群的多样性，引入差分进化算法学习策略；

3）针对BSA 收敛速度较慢的问题，引入自适应权值策略提升算法收敛速度；

4）采用混沌精英学习策略，提升种群局部搜索的能力。

1 光伏系统组件数学模型

目前已有多个光伏模型描述了太阳能电池和光伏组件的伏安特性。其中，单二极管模型和双二极管模型在实际应用中最为普遍。

1.1 太阳能电池模型

1）单二极管模型。

单二极管模型由于简单、准确等优点，被广泛用于描述太阳能电池的静态特性。图1 给出了单二极管模型的等效电路图。

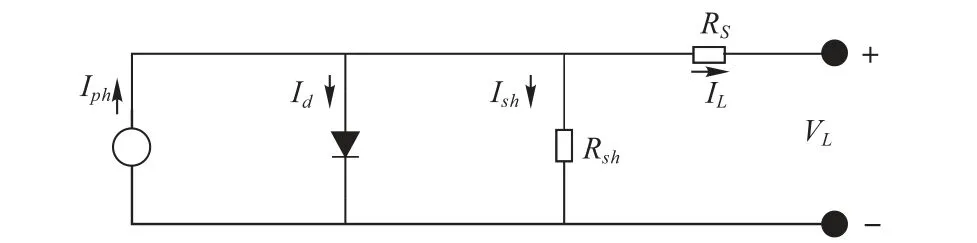
图1 单二极管模型的等效电路图Fig.1 Equivalent circuit diagram for single diode model

该模型由并联于二极管的电流源、表示泄漏电流的分流电阻和表示负载电流相关损耗的串联电阻组成。输出电流由式（1）计算：

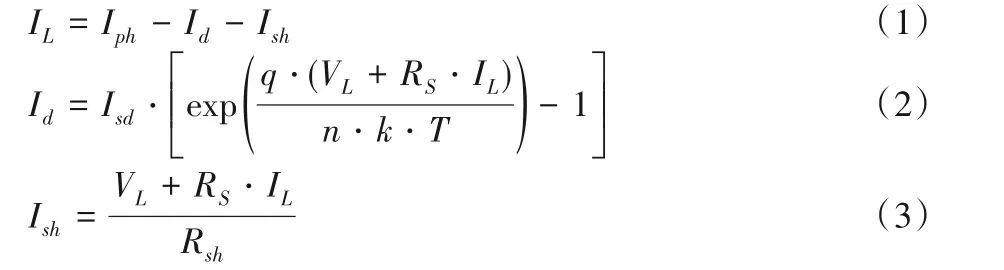
其中：IL为输出电流；Iph为光生电流；Id是二极管电流；Ish是并联电阻电流；Isd为二极管的反向饱和电流；RS和Rsh分别表示串联电阻和分流电阻；VL为输出电压；n为二极管理想因子；k为玻尔兹曼常数（1.380 650 3×10-23J/K）；q为电子的电荷量（1.602 176 46×10-19C）；T为电池的开尔文温度。因此，式（1）可改写为式（4）：

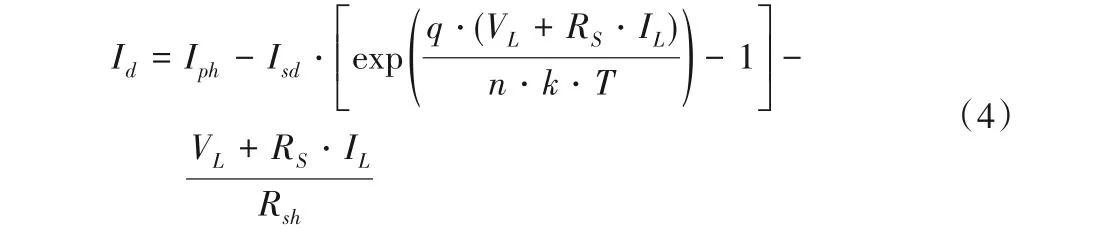
由式（4）可知，单二极管模型有5 个未知参数（Iph，Isd，RS，Rsh，n）。这些参数的准确估计对反映太阳能电池的性能具有十分重要的意义。

2）双二极管模型。

上述单二极管模型忽略了损耗区复合电流损耗的影响，如果考虑损耗，可以得到更精确的双二极管模型。该模型具有两个与电流源并联的二极管和一个用于分流光生电流源的分流电阻。一个作为整流器，另一个用来模拟电荷复合电流。双二极管模型的等效电路如图2所示。

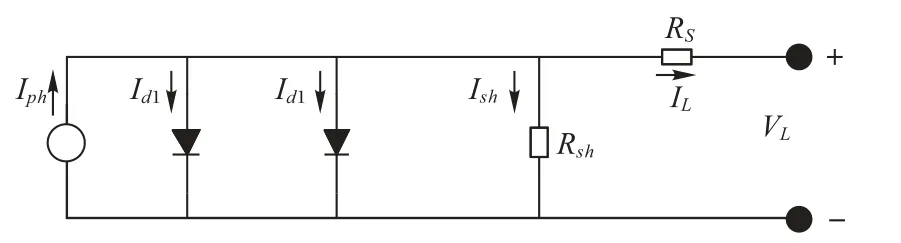
图2 双二极管模型的等效电路Fig.2 Equivalent circuit diagram for double diode model

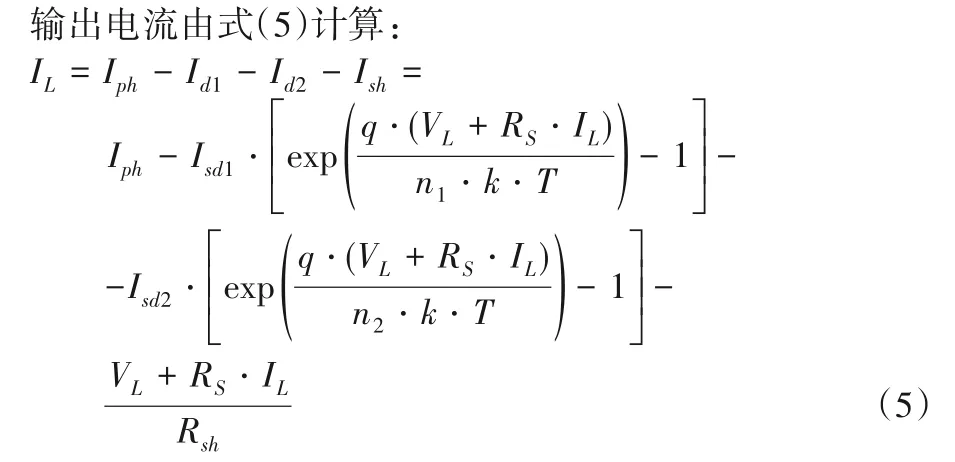
其中：Isd1和Isd2分别表示扩散电流和饱和电流；n1和n2分别代表了扩散和复合二极管理想因子。由式（5）可知，双二极管模型涉及7 个未知参数（Iph，Isd1，Isd2，RS，Rsh，n1，n2），它们需要准确识别才能获知太阳能电池的实际行为。

1.2 光伏模块模型

光伏组件模型通常包含几个串联或并联的太阳能电池。图3给出了单个二极管光伏模块的等效电路。

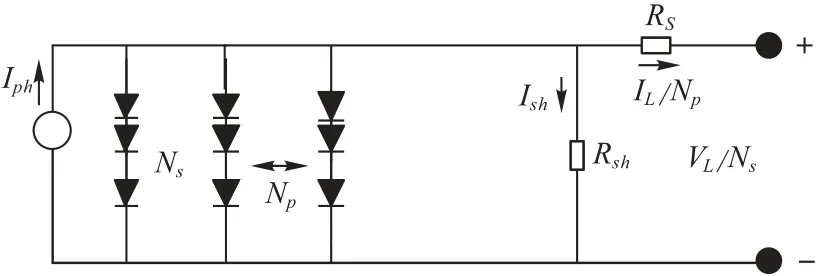
图3 光伏模块模型的等效电路Fig.3 Equivalent circuit of photovoltaic module model

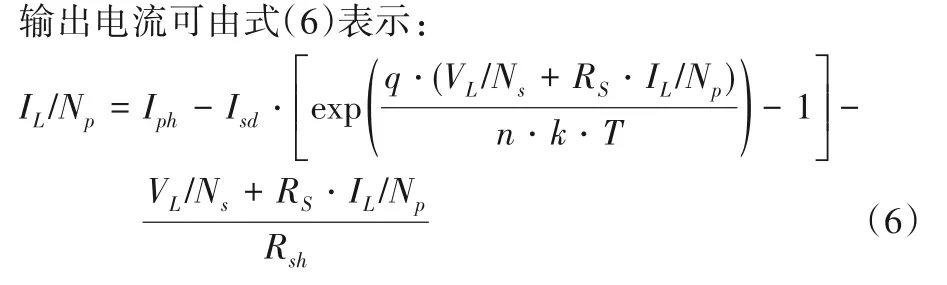
其中：Np表示并联的太阳能电池数量；Ns表示串联的太阳能电池数量。与单二极管模型相同，光伏模块模型也需要估计5个未知参数（Iph，Isd，RS，Rsh，n）。

1.3 目标函数

对于光伏模型的参数辨识问题，其主要目的是寻找未知参数的最优值，使实测数据与计算电流数据的差值最小化。因此，需要给出每一对测量和计算的电流数据点的误差函数。式（7）和式（8）分别适用于单二极管模型和双二极管模型。然后通过式（9）定义的均方根误差（Root Mean Squared Error，RMSE）对总体差异进行量化，将RMSE 作为目标函数。因此，在本文中，优化过程是通过调整每一代的解向量x来最小化目标函数RMSE（x）。

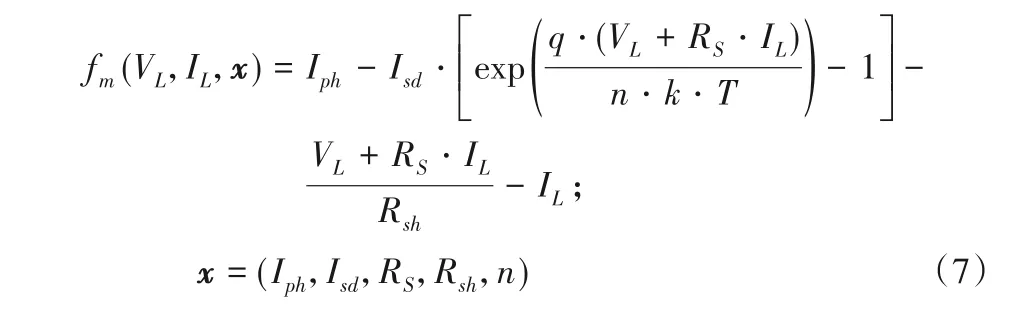
2 改进回溯搜索算法

本文提出的改进回溯搜索算法基本框架如算法1 所示。首先对种群进行初始化，并评估个体的适应度，然后采用BSA选择机制重新定义历史种群，并采用个体适应度量化排队机制计算个体的概率，根据不同的概率值采用不同的策略产生新的子代个体，最后执行混沌自适应精英搜索策略强化局部搜索，直到满足停止条件。

2.1 初始化种群

在搜索空间内随机初始化当前种群与历史种群：

其中：i=1，2，…，NP，NP是种群的大小；j=1，2，…，D，D是变量的维数；upj和lowj是分别是第j个变量的上下限；rand是［0，1］内随机分布的随机数。

2.2 BSA选择机制

在每次迭代开始时，通过式（12）重新定义历史中群oldP，并通过式（13）随机改变历史中群中的个体顺序：

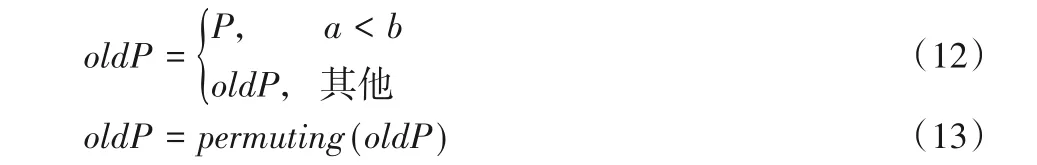
其中：a和b是0 和1 之间的两个均匀分布的随机数；permuting是将序列打乱顺序的函数。

2.3 个体适应度量化排队机制

针对算法在搜索过程中存在全局搜索与局部搜索能力的不均衡问题，本文算法引入文献［9］中个体适应度量化排队机制。即个体在整个种群中的表现是通过概率来量化的，排序的原则是适应度高的个体具有较大的概率，而适应度低的个体具有较小的概率，每个个体可以根据其概率自适应地选择属于自己的进化策略，以提高全局搜索与局部搜索能力。特别地，适应度较差的个体进行局部搜索，而较优的个体进行全局搜索。

首先，种群中的个体根据适应度值按升序排序（从最好到最差）。根据式（14）计算第i个个体的排名，然后根据每个个体的排名，用式（15）计算出每个个体的概率，适应度高的个体有着较大的概率。

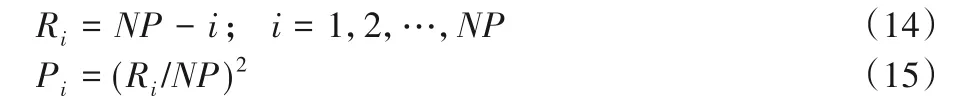
其中：NP是种群的大小；R是一个序列，代表每个个体的排名；Pi是在［0，1］范围的浮点数，表示第i个个体的概率。

2.4 基于自适应权值的进化策略

在BSA中，没有考虑最优个体对于局部搜索的引导作用，个体可能无法快速找到由最优个体引导的搜索区域，这会导致BSA 的收敛速度较慢。而在IJAYA 算法中，主要引入了自适应权值来调整趋近最优解和远离最差解的趋势。在JAYA算法的搜索过程中，期望种群在搜索空间的早期阶段接近有希望的区域，在搜索后期阶段进行局部搜索，以提高种群的质量。因此，Yu等［11］引入式（16）中的权值来调整最优解的趋近程度和最差解的避免程度，进而得到改进的更新方式见式（17）：

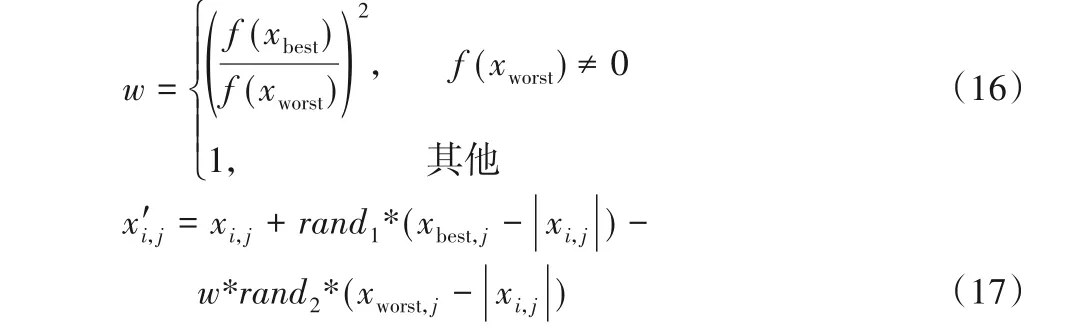
其中：xbest、f(xbest)分别为种群中的最优解及其适应度函数值，xworst、f(xworst)分别为最差解及其适应度函数值；xi，j为第i个候选解的第j个变量的值，x′i，j是xi，j的更新值；rand1和rand2分别为［0，1］区间内的随机数。可以看出，引入的权重因子可以自适应调节。随着搜索过程的进行，最优解与最差解之间的函数值差越来越小，权值逐渐增大。因此，在早期，由于w值较小，当前趋势主要是接近最优解；随着搜索的进行，w值越来越大，开始越来越侧重局部收敛，不仅可以继续接近最优解而且可以不断远离最差解。

2.5 差分进化学习策略

在BSA中变异阶段只是单纯利用历史种群来进行更新新个体，这使得在迭代的过程中，种群的多样性会迅速下降。针对这一缺点，本文算法引入差分进化学习策略，对当前种群也进行差分进化学习，期望借助此方法提高种群多样性。因此，改进的公式如式（18）所示：

其中：Vi，j是产生的新个体；Ph，j、Ph′，j和Ph′′，j是在现有种群中随机挑选的三个互不相同的个体；oldPi，j与Pi，j分别是历史种群与现有种群中的个体；mapi，j是一个大小为NP*D的二进整数值矩阵，元素值由混合率参数（mix rate）控制，混合率参数一般取1，它被用来引导交叉方向；F是控制搜索方向矩阵振幅的尺度因子，其值通常设置为3*randn，其中：randn～N(0，1)，即randn为服从均值为0，标准差为1的正态分布的随机数；F1是自适应的变异系数。F1的计算公式如下：

2.6 自适应的混沌精英搜索策略

为了进一步提高种群的质量，本文算法引入文献［9-11］中的自适应混沌精英搜索策略，在当前的最优解附近寻找新解，然后将这个新解代替最差解。

在该搜索策略中，最优解吸引其他个体靠近，从而逐步地提高全体种群的质量。但是光伏模型参数识别是典型的非线性多模态问题，其最优个体经常处于局部最优，它如果持续吸引其他个体，就会造成整个种群早熟收敛。而混沌序列具有随机性与便利性，这对通过生成新的解来进一步提高种群的质量非常有帮助。这里使用的混沌序列是使用logistic 映射所得到的，如式（20）所示：

在搜索的早期，需要在最优解附近尽可能地搜索，拓展空间，增强全局搜索能力；而在搜索后期需要深入探索，加快收敛速度。采用式（21）产生最优解附近的新解：

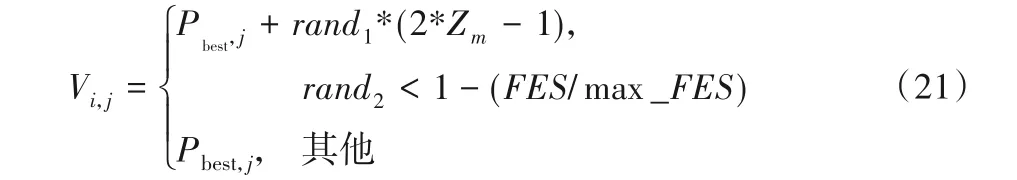
其中：m为迭代次数；Zm为第m次混沌迭代的值，其初始值Z0在［0，1］中随机产生。rand1和rand2是两个［0，1］范围内的随机数。

2.7 MBSA的时间复杂度分析

在时间复杂度上，BSA 的时间复杂度为O(Gmax*(NP*D)，与原始的BSA 相比，MBSA 的额外复杂度主要来自于个体适应度量化排队机制、基于IJAYA算法的改进策略、差分进化学习策略和自适应的混沌精英搜索策略。O(2*(NP-1))是引入的IJAYA 算法中寻找最优个体和最差个体的花费，计算每个个体概率的花费是O(NP)，种群中所有个体排序的花费是O(NP*log(NP))，实现混沌精英搜索策略的花费是O(D)，Gmax为适应度最大评价次数。MBSA 的总的时间复杂度为：O(Gmax*(NP*D+D+NP*log(NP)+2*(NP-1) +NP))。一般来说，种群大小NP与待求解问题的维数D成正比，因此根据时间复杂度运算规则，MBSA 的时间复杂度为O(Gmax*NP*D)，与BSA的时间复杂度相同。

3 实验与结果分析

3.1 实验参数设置

为验证算法在解决参数识别问题的有效性，本文采用实验电流电压数据［20］作为基准数据对算法性能进行验证。表1给出了各参数的取值范围，为保证实验公平性，本文中实验所比较的算法涉及的参数取值范围均保持一致。为消除种群大小对于各个算法性能的影响，本文统一将各算法的种群大小设置为50，而MBSA 的引入的参数F0设置为0.6、混合率参数（mix rate）设置为1。每个算法设置最大函数评价次数为50 000，每个算法独立运行30次。在比较结果中，所有算法的总体最佳RMSE值用粗体标记。

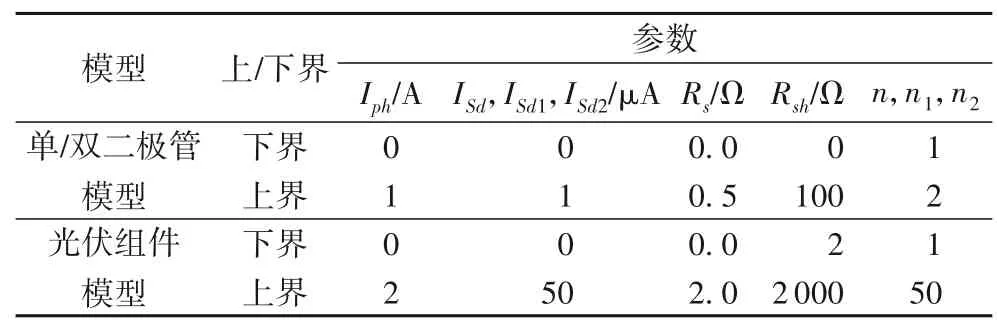
表1 光伏电池（RTC，France）和光伏组件（Photo Watt-PWP 201）的参数范围Tab.1 Parameter ranges of photovoltaic cell（RTC，France）and photovoltaic module（Photo Watt-PWP 201）

3.2 本文所提策略的有效性分析

为了测试本文所提策略的有效性，对算法中引入的策略进行了验证。本节中以BSA 为基本算法，逐步添加所引入的策略。将个体适应度量化排队机制称为A、将基于IJAYA 算法的改进策略称为B、将差分进化学习策略称为C、将自适应的混沌精英搜索策略称为D。图4 展示了参与对比的5 种算法在单二极管模型上独立运行30 次的RMSE 均值的收敛曲线，其中BSA+A+B+C+D 即为本文提出的MBSA。表2 是5 种对比算法在单二极管、双二极管以及光伏模型上获得的RMSE的均值和标准差结果。

表2 不同算法在单二极管、双二极管和光伏组件模型上获得的RMES结果Tab.2 RMES results of different algorithms on single diode，double diode and photovoltaic module models

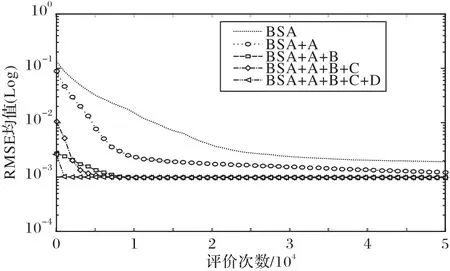
图4 不同算法在单二极管模型上的收敛图Fig.4 Convergence diagram of different algorithms on single diode model

从图4 中对比可以明显看出，通过引入四种策略，算法整体的收敛速度和准确性都在逐渐稳步提升。可以看到基准的BSA 表现最差。通过添加个体适应度量化排序机制使每个个体可以根据其概率自适应地选择属于自己的进化策略，从而提高了寻优速度，从图4 中可以明显看到其收敛速度有了很大提升。而基于IJAYA 算法的改进策略旨在增强算法的局部收敛能力，结合表2 数据中单二极管模型对应的数据中可以看到，算法的准确性以及稳定性得到了进一步提升。差分进化学习策略意图通过差分学习进一步增加种群多样性，结合其对应的单二极管模型的仿真数据可以看到，此时算法的全局寻优能力有明显提升。最后，在此基础上添加解决整个种群早熟收敛的策略，由于其策略中独特的随机性混沌序列，使算法增加跳出局部最优解的能力。如表2 所示，算法的稳定性得到了进一步的提升。综上，文中引入的策略从算法的收敛性和多样性上对BSA 起到了提升作用，提高了算法的寻优能力和结果的稳定性。

3.3 与先进算法对比分析

为了进一步验证算法的有效性，本文选取了八种先进算法与本文所提算法进行比较，包括：BSA［15］、MLBSA［10］、TLBO［14］、LCJAYA［8］、PGJAYA［9］、IJAYA［11］、STLBO［7］、JAYA［21］。其中与BSA 和MLBSA 的对比用于测试本文所提策略对BSA的改进效果，而其余几种算法则是目前在求解光伏模型参数识别问题上表现较好的算法。

在比较结果中，所有算法的总体最佳RMSE 值用粗体标记。如表3 所示，在单二极管模型的实验中，算法MBSA、PGJAYA、MLBSA 得到了最小RMSE 值9.860 2E-04，但是这三种算法中MBSA 的RMSE 值最小，意味着其可靠性最高。而在双二极管模型的实验中，只有MBSA 得到了最小RMSE值9.857 6E-04，剩下的几种算法中只有PGJAYA 算法得到的最小RMSE 值9.867 2E-04 与之最接近，但是MBSA 比PGJAYA 算法的整体表现要好得多，可靠性也很高。最后，在光伏组件中，得到最小RMSE值2.425 1E-03的算法有MBSA、LCJAYA 和STLBO，然而，在这三种算法中只有MBSA 的可靠性更高、更稳定。

为了直观地表示不同算法在30 次运行中得到的结果分布，图5 给出了每个算法的箱线图。通过比较每个算法的最佳RMSE 值的箱线图的分布情况，可以清晰地看出MBSA 的准确性与鲁棒性明显优于其他用于比较的八种算法。

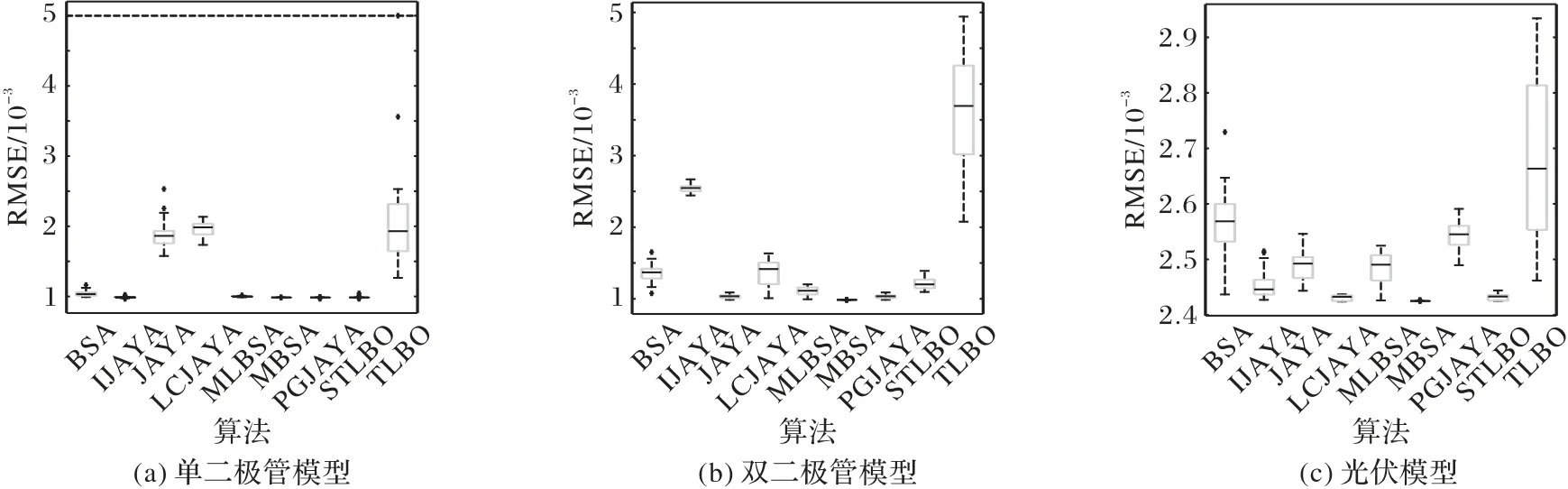
图5 光伏电池和光伏组件运行30次下九种算法的最佳RMSE值的箱线图Fig.5 Boxplot of optimal RMSE values of nine algorithms under 30 runs of photovoltaic cell and photovoltaic module

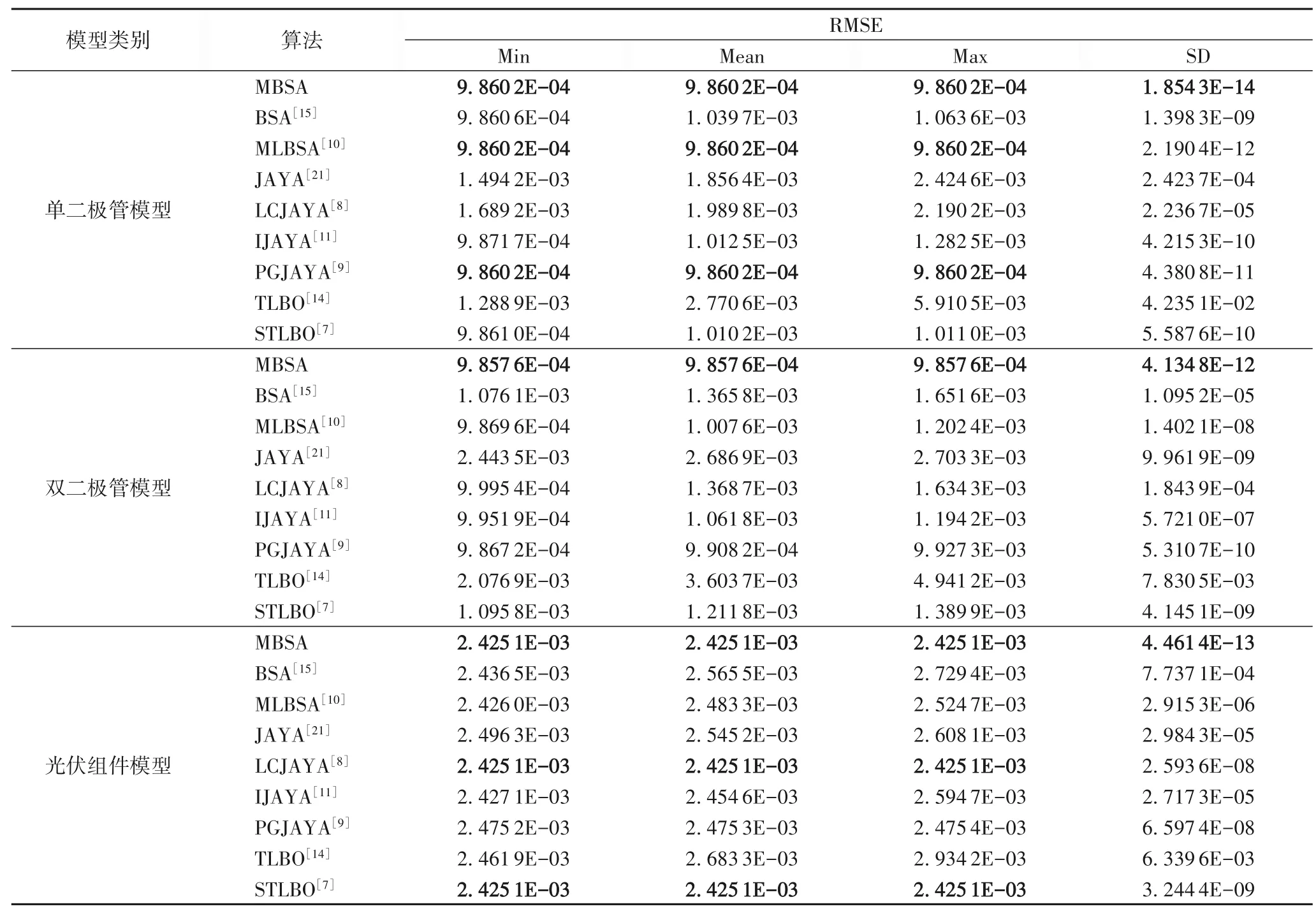
表3 光伏电池（RTC，France）和光伏组件（Photo Watt-PWP 201）的计算结果Tab.3 Calculation results of photovoltaic cell（RTC，France）and photovoltaic module（Photo Watt-PWP 201）

3.4 来自厂家数据表的实验数据结果

为了进一步评价所提MBSA 的可靠性，本节利用从三个不同类型的光伏组件制造商的数据表中获得的真实数据对算法进行实际测试。实验涉及的三种不同类型的光伏组件是：薄膜（ST40）、单晶（SM55）和多晶（KC200GT）［22］。使用的实验数据直接从厂商数据表中给出的五种不同光照水平（1 000 W/m2、800 W/m2、600 W/m2、400 W/m2、200 W/m2）和不同温度水平下的电流电压曲线中提取。

未知参数的范围是Iph∈[0，2*Isc]，ISd∈[0，100]，Rs∈[0，2]，Rsh∈［0，5 000］，n∈[0，4]。如式（22）所示，非标准实验条件下的Isc由标准实验条件（Standard Test Condition，STC）下的数据表参数决定：

其中：Isc_stc为短路电流；α为短路电流的温度系数；G和T分别代表光照水平和温度。

如表4所示，MBSA 在25℃不同光照条件下对三种光伏组件预测了最佳参数，因为没有准确的参数值来验证得到的参数，于是绘制了三种光伏组件在25℃不同光照水平下的I_V特性曲线，如图6 所示。在图6 中，可以清晰地看到预测数据与实测数据的拟合程度非常高，验证了MBSA 在三种光伏组件仿真实验中的准确性。

如表5 所示，MBSA 在1 000 W/m2光照强度下，对三种光伏组件进行了最优参数预测。如图7所示，绘制了1 000 W/m2光照强度不同温度下的I_V特性曲线，同样地，预测数据与实测数据二者十分接近。

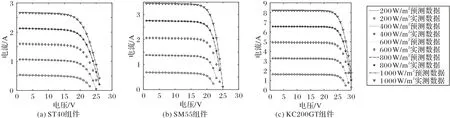
图6 三种光伏组件在不同光照强度下预测数据与实测数据的比较结果Fig.6 Comparison between predicted data and measured data of three photovoltaic modules under different illumination intensities

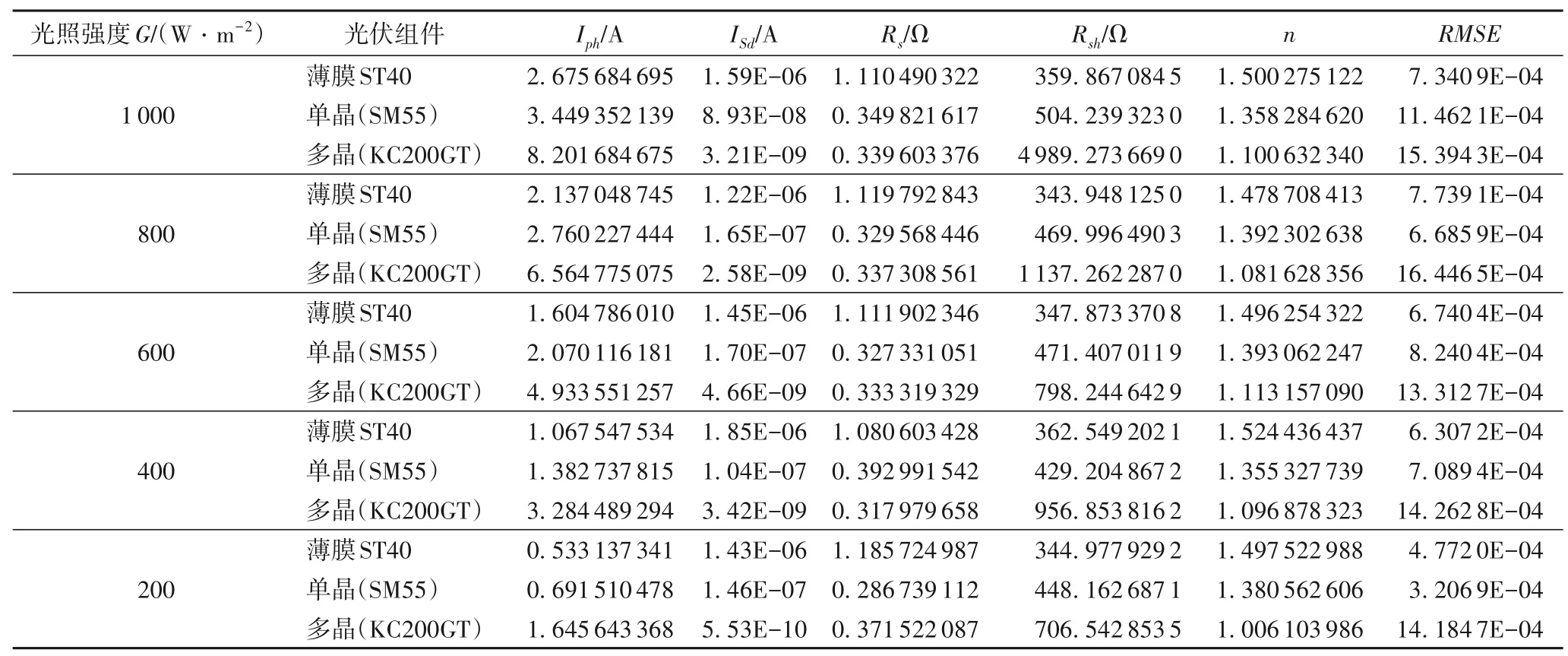
表4 MBSA在25℃不同光照条件下对三种光伏组件的预测的最佳参数结果Tab.4 Results of optimal parameters predicted by MBSA for 3 photovoltaic modules under different illumination conditions at 25℃

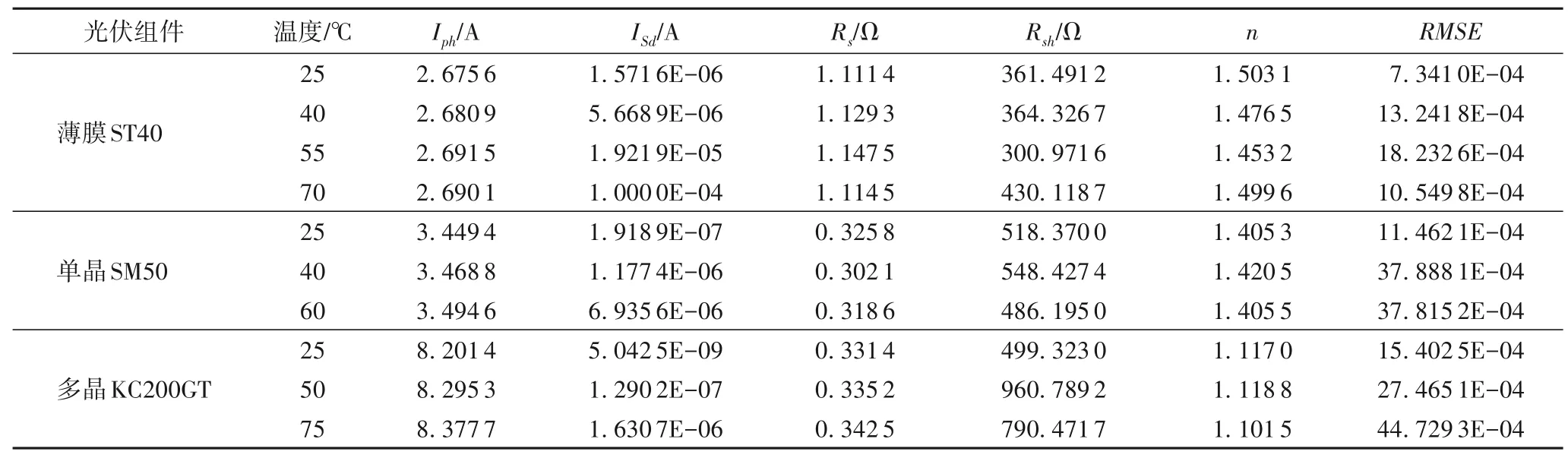
表5 MBSA在1 000 W/m2和不同温度条件下对三种光伏组件的预测最佳参数的结果Tab.5 Results of optimal parameters predicted by IJAYABSA for three photovoltaic modules under 1 000 W/m2 and at different temperatures

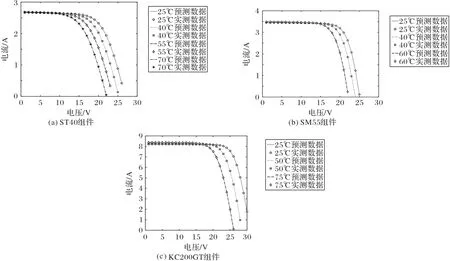
图7 三种光伏组件在不同温度下预测数据与实测数据比较Fig.7 Comparison between predicted and measured data of three photovoltaic modules at different temperatures

4 结语

本文提出了一种基于IJAYA 算法的改进回溯搜索算法（MBSA）识别光伏模型参数。首先，利用排序量化个体在种群中的表现为每个个体分配一个概率，在此基础上，每个个体自适应地选择合适的进化策略，增强相应的搜索能力；其次，根据随机概率同时学习历史种群信息和当前种群信息，并运用差分进化算法对当前种群进行进化变异，以增强种群多样性；再者，运用IJAYA 算法在向最优个体靠近的同时还远离最差个体，并且IJAYA 算法特有的参数帮助算法在早期阶段接近潜在区域，在后期阶段实现局部搜索的特点，来增强算法的挖掘能力和提高算法的收敛速度；最后，运用混沌精英学习策略利用当前最优解搜索出更好的解来代替最劣解，以提高每一代种群的质量。通过在单二极管、双二极管和光伏组件模型的参数识别的仿真实验验证算法的性能，并与现有的其他八种优秀算法进行比较分析表明了本文所提算法的优越性。最后根据真实厂商数据，在三种不同类型的光伏组件上进行不同光照强度和不同温度的实验，进一步检验MBSA 的有效性。综上所述，本文所提的算法具有一定的竞争力和优越性，预期可广泛地应用到其他领域的参数识别问题当中。