基于负荷平衡的电动汽车模糊多目标充电调度算法
周美玲,陈淮莉
(上海海事大学物流科学与工程研究院,上海 201306)
0 引言
随着化石能源消耗的日益增长和新能源技术的发展,电动汽车(Electric Vehicle,EV)迅速发展起来。但EV充电负荷使电网负荷“峰上加峰”,导致配电网线路过载、三相不平衡等问题。三相不平衡会影响用电设备的安全运行,不利于电网的安全运行和电力系统的可靠稳定,因此需引导EV的充电行为,以提高配电网接纳EV的安全性与稳定性。
EV 充电调度策略按控制策略分为分散式充电和集中式充电[1]。分散式的核心是对单辆EV 优化[2],但在平抑负荷波动和把握系统全局信息方面存在不足。集中式充电基本服务于居民小区[3],部分学者并没有考虑三相不平衡对电网的影响,而是以等效的单相系统或假设三相平衡为前提,从用户、充电站和配电网的角度来研究问题,以用户充电成本最小化[4]、用户充电满意度最大[5-6]、配电网运行成本最小化[4,6]、运营商利润最大[7]、平滑负荷曲线[5,8]等为优化目标,建立含不同约束的混合整数单目标或多目标模型,再用遗传算法、粒子群算法等进行求解。由于充电站的不同约束,计算成本最小化或用户满意度最大化等目标的可行时间表不能有效减小峰谷负荷差[9],甚至会造成另一个高峰。
黄小庆等[5]和Singh 等[10]研究了EV 充电对三相不平衡的影响,认为负荷应在三相之间合理分配。基于此,占恺峤等[11]提出了以控制三相负荷平衡和降低网损为目标的充电调度策略,但并不能满足实时充电需求。李佩杰等[12]引入滚动时域控制理论提出实时调度策略,采用内点法求解来控制三相负荷,但当EV 规模较大时,由于模型维数较高不能满足实时优化要求。Hernández-Arauzo 等[13]则提出将三相问题分解成三个实体从而解决一个个排序问题来实现三相平衡。上述文献虽可以降低三相不平衡度,但是未考虑EV实时充电所导致的负荷峰谷差以及能量分配的公平性。
在求解多目标问题上,思路有:1)对多目标进行加权求和转化为单目标[14]求解,但是权重的选择标准难以确定和具有主观性;2)基于帕累托最优解集得到Pareto 最优前沿,不求折中解或通过目标权重法[15]等指标获得折中解。改进非支配排序遗传算法-Ⅱ(Non-dominated Sorting Genetic Algorithm-Ⅱ,NSGA-Ⅱ)是求解多目标的进化算法,在求解多目标问题上被广泛应用。
针对上述问题,本文将三相不平衡度和负荷峰谷差视为一种约束,提出一种考虑负荷平衡的电动汽车多目标充电静态和在线调度策略。通过滑动窗口得到EV 的充电时间并生成可行时间表,使得总延迟时间最小且尽可能实现公平充电。本文采用改进NSGA-Ⅱ算法进行求解,通过模糊隶属度方法在Pareto 最优前沿面中得到最优折中解。最后以某小区为例,对本文所提模型和策略进行验证。
1 电动汽车充电调度模型
本文研究在小区停车场充电的私家EV,假设用户在私人停车位加充电桩充电,EV 充电的地点以及所在相固定。假设该停车场有M个停车位,每条停车线Li有Mi个充电点。在停车场每个私人停车位都有一个充电点,连接到一个单相,当它有效时以恒定的功率进行充电,充电控制架构如图1所示。

图1 电动汽车有序充电控制架构示意图Fig.1 Schematic diagram of electric vehicle orderly charging control architecture
当用户到达停车场接入智能充电桩,充电桩读取EV到达时间和电池剩余电量,用户输入期望离开时间,中央控制器通过本文调度策略安排EV的充电时间。其中,通过限制每条线路上可以同时充电的电动汽车数量N来平抑负荷波动,通过将三相负荷不平衡度Δ作为约束,使得三条线路的负荷在所设置的范围内。
1.1 静态调度模型
1.1.1 问题描述
在静态模型中,问题表述如下:考虑三条线路Li(i=1,2,3),每条Li上有mi车辆到达,车辆被表示为:已知EV 到达时间tij≥0,充电时间pij>0,以及期望离开时间dij。根据文献[8-9]可知在18:00—21:00负荷叠加后会超出变压器总量,甚至会超出总量的10%左右,威胁电网安全运行。为简化计算,18:00—21:00 的可同时充电的电动汽车数量设为N-5,从而减少该时间段的充电车辆。
1.1.2 目标函数
模型同时考虑两个优化目标,具体如下:
1)目标1。
该充电策略是为得到可行时间表,为车辆vij分配决策变量的充电时间xij(i=1,2,3,1 ≤j≤mi),并得到车辆的充电完成时间Cij,即xij中的最后一个充电时间。目标函数是总延迟时间最小化,定义如下:

2)目标2。
由于部分EV 可能无法充满,因此应尽可能公平充电,将EV 在期望离开时间之前的充电量与所需总充电量的比值的差值的绝对值Xij的总和最小化作为另一个目标,如下所示:

其中:Tij是车辆vij进行充电的所有时间段;t'为在期望离开时间之前的时刻;xijt是车辆vij在一个时间段的充电量分别是vij在期望离开时间之前得到的充电量和所需总充电量。
1.1.3 约束条件
1)车辆vij在一个时间段ΔT的充电量xijt。

其中:u为额定充电功率;η为充电效率。
2)车辆vij的充电量不大于其需求Dij。

3)车辆只能在其可用的充电时间段内充电。

4)每条线路上车辆的开始充电时间stij不能小于它的到达时间tij。

5)在t时刻,Li线路上的车辆同时可活动充电点数量Ni(t)不得超过N。
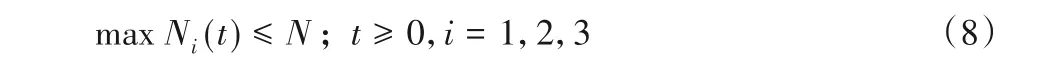
通过限制线每条线路上每个时间段的同时充电车辆数量,降低每个时间段的负荷峰值,从而减小负荷峰谷差。
6)在t时刻,用任意两条线路上同时充电的车辆数量差与N的比值来衡量三相不平衡度,Δ为最大允许的三相不平衡度。

对EV进行调度时,选择该线路在车辆分配充电时间段与其他线路计算得到的三相不平衡度最大值与Δ比较,若不符合式(9)则重新安排开始充电时间,直到约束得到满足。
1.2 在线调度模型
在实际情况中,车辆的到达时间和充电时间是未知的,因此是在线调度问题。在线调度问题可以看成是每个时刻下产生的静态问题实例P1、P2、…、Pn。
在时间Tk上的实例Pk由已经到达充电站但还未开始充电的车辆和已经在充电的车辆组成,车辆可表示为{vi1,vi2,…,viai,…,vimi}。已知vij的充电时间pij和期望离开时间dij。其中一部分车辆(vi1,vi2,…,viai)在充电,但未充完,即对所有车辆1 ≤j≤ai,满足Cij>Tk和stij>Tk。剩下的车辆(viai+1,viai+2,…,vimi)尚未开始充电。
在给定时间t中的实例Pk中,在Li上可为新车辆充电的容量按以下方式计算:
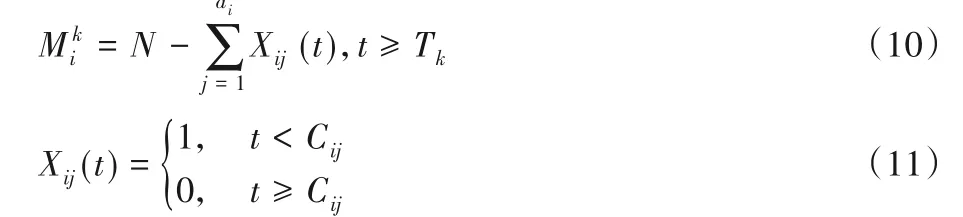
该充电策略是为在Tk上的Pk中的EV 分配满足静态问题所有约束的充电时间x'ij,得到该Pk的可行时间表。
考虑到无法预测未来EV的接入时间和充电需求,因此本文按Tk-1-Tk=ΔT(10 min)建立144 个时段,并采用滑动窗口方案[17],如图2所示。
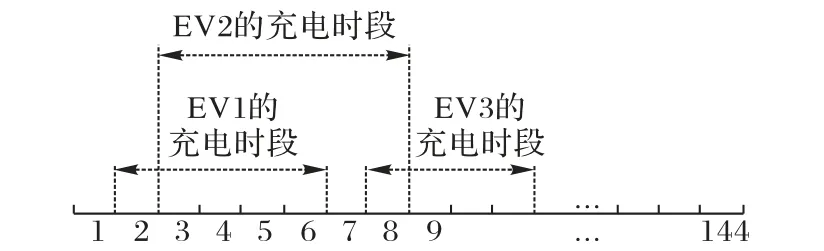
图2 控制时段示意图Fig.2 Schematic diagram of control period
在每个Tk内,控制系统监测在[Tk-1,Tk]内的到达车辆来创建Pk,并检查该时间段EV 的充电信息,再为随后的调度定义新的滑动窗口。新的滑动窗口被定义为满足N和Δ约束的新EV 到达和正在充电的EV 的最新可用充电时间之间的时间。随后,控制系统根据新的滑动窗口得到新的解决方案sk,而sk会取代之前的解决方案sk-1。若车辆未能在期望离开时间之前完成充电,则生成满足约束的开始充电时间进行充电直到充满。在Tk内,只要车辆还没有充电,可以在不同的Pk中分配不同的x'ij。一旦该车辆正在充电,该车辆的x'ij就不能再改动。
2 模型求解
2.1 改进的NSGA-Ⅱ算法
对于该模型而言,决策变量是车辆充电时间。改进非支配排序遗传算法Ⅱ(NSGA-Ⅱ)的特点是对种群进行非支配排序和拥挤度计算,生成子代后选择父代与子代中的优先个体作为新种群,最后得到Pareto最优解集。主要内容如下:
2.1.1 编码方法
本 文 用A={ai,j,t|i∈[0,3],j∈[0,Mi],t∈[0,144],i,j,t∈N}来描述EV 的分配状况,ai,j,t表示在线路i上第j辆EV是否在t时刻正在充电。
2.1.2 种群初始化
根据规则和约束(7)随机生成初始种群,依次将EV 分配到充电位置,若正在充电,则令ai,j,t=1。
传统的NSGA-Ⅱ算法中初始解的构建是随机的,因此本文运用顺序贪婪随机(Sequential Greedy Stochastic,SGS)算法分配EV的充电时间,得到初始解。
为了尽量减少延迟时间,在每个时间表α中未充电车辆的最早可能充电时间为E(α),所有没有安排充电的车辆即ai,j,t=0时在E(α)时充电的选择概率Πj为:
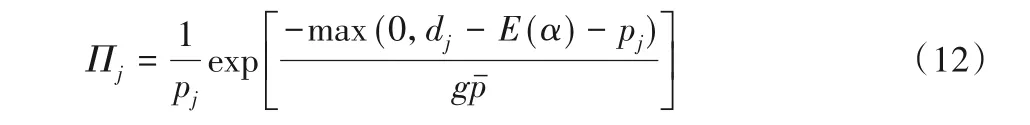
为得到不同的解决方案,首先对选择概率按升序对所有车辆进行排序;然后执行竞赛选择,选择tSize数量的随机车辆并从中取出最优个体放入到列表中,从而得到优先级列表;最后遍历列表,按列表中顺序为车辆分配满足所有约束的尽可能早的充电时间,从而得到初始解。其中,tSize若较小会导致几乎随机的解,而较大的值会产生相似的解,因此本文设置tSize=8。
在该算法下,一定可以获得一个满足所有约束的初始解,在最坏的情况下即将EV的最大完成时间作为开始充电时间。因此,在N>0和Δ>1/N的情况下,得到可行时间表。
2.1.3 适应度函数和选择算子
适应度函数F=1/f,在选择过程中,将父代和子代种群合并进行非支配排序和拥挤度计算,从中选取最优个体组成新种群进行交叉、变异等操作。
2.1.4 交叉算子
本文比较三种交叉算子并选择最优的一种,交叉策略如下:
1)单点交叉。随机选择染色体的位置,对在p1、p2中选择该位置的车辆进行交叉,产生o1、o2。
2)基于到达时间的交叉算子。生成随机数x,若x<pc,则随机选择到达时间t0,在p1中选出到达时间大于t0的车辆,按照这些车辆在p2中出现顺序放在o1的末尾,o2也是如此创建。图3展示了该交叉方式的操作,假设p1中车辆到达时间为(9,11,10,15,17,16,18,18,21,17,17),p2为(9,11,17,16,21,10,18,17,18,15,17)。随机选择到达时间t0=17,则子代如图3所示。
3)基于离开时间的交叉算子。随机选择到达时间t1,在p1中选出到达时间大于t1的车辆,按照这些车辆在p2中出现顺序放在o1的末尾,o2也是如此创建。

图3 基于到达时间的交叉算子Fig.3 Crossover operator based on arrival time
2.1.5 变异算子
采用自适应变异概率,若f>favg,pm=0.1;否则pm=0.01。若下一代最优个体适应度值大于当前最优个体适应值,则用轮盘赌法保存最优个体,替代较差个体。
2.1.6 外部档案集合
通过设置一定容量的外部档案以保存先前找到的帕累托最优解,每次通过判定是否被外部档案内个体支配和是否支配外部档案个体来迭代和更新Pareto 最优解集。当外部档案的大小超过上限时,则根据拥挤度对外部档案执进行轮盘赌选择存入外部档案集合的解。
2.1.7 拥挤度判定
过于拥挤或稀疏的Pareto 解集不利于选取折中最优解,因此采用拥挤度判定使Pareto前沿面更均衡,公式为:

其中:z为目标函数个数;a、c分别为待拥挤判定解b的相邻解。
2.2 Pareto前沿面的最优折中解
本文所求是目标值最小,因此采用偏小型模糊隶属度函数[18],再计算Pareto 最优解集中各最优决策满意度,函数值越大则满意程度越高,满意度最高的解将作为折中解,模糊隶属度函数为:
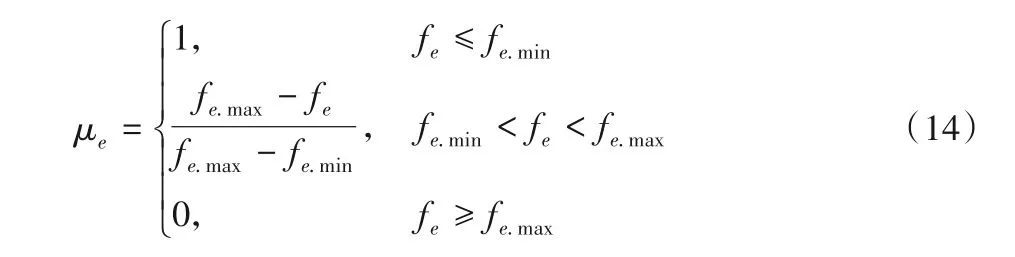
其中:fe.min、fe.max为在满足约束条件下的目标函数最小值、最大值;e=1,2。利用满意程度作评价标准,公式为:

其中:Y表示最优解个数;μs表示标准化条件下第s个最优解的满意度。
2.3 局部优化
由于约束(9)中最大三相不平衡的约束会导致一些EV分配到不理想的充电时间,因此本文运用局部优化方法[14]进行改进,如图4所示。
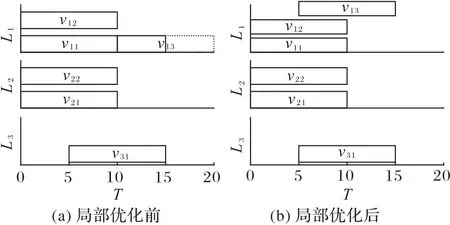
图4 局部优化示意图Fig.4 Schematic diagram of local optimization
假设N=3,Δ=2/3;v31的到达时间为5,其他车辆的到达时间为0;所有车辆充电时间为10;v13、v31的期望离开时间为15,其他车辆离开时间为10。对车辆进行排序得到排列V(v11、v12、v21、v22、v13、v31)。
先对前四辆EV进行调度,再根据约束(9)可计算出在[0,10]内ΔL13=2/3,若v13的开始充电时间为0,则在[0,10]内ΔL13=1>2/3,因此需对v13重新调度,其开始充电时间为10。按顺序对v31进行调度,其开始充电时间为5,此时总延迟时间为5,如图4(a)所示。但v31的调度使得在[5,10]内ΔL13=1/3,因此重新给v13分配开始充电时间为5,此时ΔL13=2/3,如图4(b),此时总延迟时间为0。
此示例说明需要运用局部优化方法,因此按下列方式重新调度车辆。当为新车辆调度时,检查Lj上充电时间为p'的可行开始充电时间为t'的电动汽车v'的调度是否会在[t',t'+p']打破先前车辆充电的不平衡限制。
当且仅当在调度之前,在Li和Lj上达到了最大不平衡限制即不能再对EV进行调度,形式上,∀t∈[t′,t′+p′]满足:

若以上约束都能满足,则意味着对v'的调度打破了[t',t'+p']的不平衡限制,则可对部分EV重新进行调度。若出现这种情况,则取消Li中所有x'ij≥t'的EV 的调度,使得在满足所有约束的前提下这些车辆的x'ij能更早。
3 算例分析
3.1 基础数据
本文以居民小区配电网为例分析,采用2009 年全美家庭出行调查(National Household Travel Survey,NHTS)的结果,车辆到达时间、期望离开时间、日行驶里程的概率密度表达式见文献[5]。
假设EV 电池容量为50 kW·h,额定充电功率u=7 kW,充电效率η=0.92;电动汽车数量M=180;假定用户期望离开荷电状态为1,用户未在充电完成时间前将车辆开走。
为说明本文模型和策略的有效性,选取两种不同类型进行测试。类型1:每条Li有60 辆车辆到达;类型2:60%到达L1,30%到达L2,10%到达L3。显然类型2 加剧线路之间的不平衡。选取4 种不平衡度值Δ(0.2,0.4,0.6,0.8)和3 种N值(20,30,40),因此总共有由类型、N、Δ组成的48种情形。
在Matlab 环境下编程,种群大小为100,交叉概率为0.9,自适应变异概率为0.1 和0.01,迭代的最大次数为120 或者找到一个零延迟的解。外部档案容量上限为种群大小。考虑到算法的随机性,运行30次得到具有统计意义的结果。
3.2 改进NSGA-Ⅱ算法参数选择
本文用非参数统计检验来分析不同参数的差异,先用SW(Shapiro-Wilk)检验数据的非正态性,再用Wilcoxon 匹配对符号秩检验计算p值来验证差异是否具有统计学意义。在这些检验中,设置置信度为95%,备择假设是“平均总延迟值之间的差不等于0”。
3.2.1 交叉概率选择
表1 列出静态和在线调度不同交叉概率pc下最优折中解下的平均总延迟时间。可看出pc=0.9 的结果优于pc=0.8 和pc=0.6,且p值都小于0.1,差异具有统计学意义。

表1 静态和在线调度不同交叉概率的平均总延迟时间 单位:hTab.1 Average total delay time of static and online scheduling with different crossing probability unit:h
3.2.2 交叉算子选择
表2 显示静态和在线调度三种交叉算子最优折中解下的平均总延迟时间,可看出基于到达时间的交叉算子能够得到更优的解,且p值都小于0.1,可知基于到达时间的交叉算子与其他算子之间存在统计学上的显著差异。

表2 静态和在线调度三种交叉算子的平均总延迟时间 单位:hTab.2 Average total delay time of static and online scheduling with three crossover operators unit:h
3.3 算法分析
为分析局部优化对解决方案的作用,图5 显示使用和不使用局部优化的总延迟时间的差值。可知在使用局部优化后结果更优。且随着Δ的增加,使用局部优化的改进量减小;在给定Δ值下,随着参数N的增加,改进量随之减小。
运用改进NSGA-Ⅱ算法得到N=20 和Δ=0.2 下的Pareto最优前沿和折中最优解,如图6(a)所示;图6(b)所示为遗传算法(Genetic Algorithm,GA)得到的Pareto 最优前沿。从图6可知,采用改进NSGA-Ⅱ算法能够得到更加完整的Pareto 最优前沿,基于拥挤度筛选后的Pareto 最优前沿更加均匀。然后采用模糊隶属度函数求解折中最优解,如表3 所示,在极端解的情况下,其他目标优化较小甚至出现劣化现象。

图5 使用与不使用局部优化的总延迟时间差值Fig.5 Difference in total delay time with and without local optimization
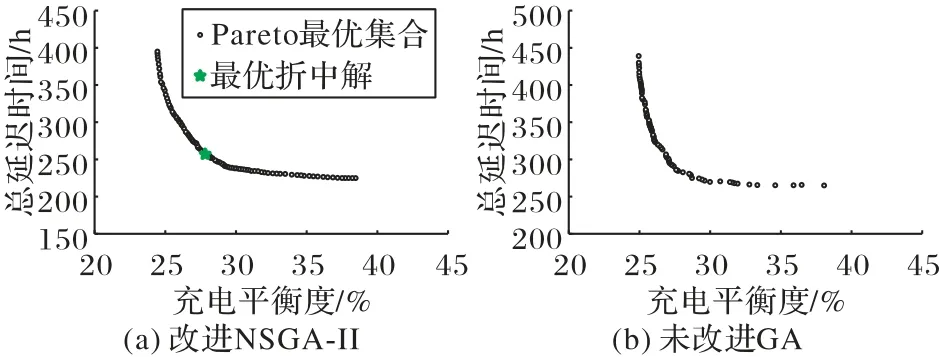
图6 两种算法的Pareto最优前沿Fig.6 Pareto optimal frontiers of two algorithms
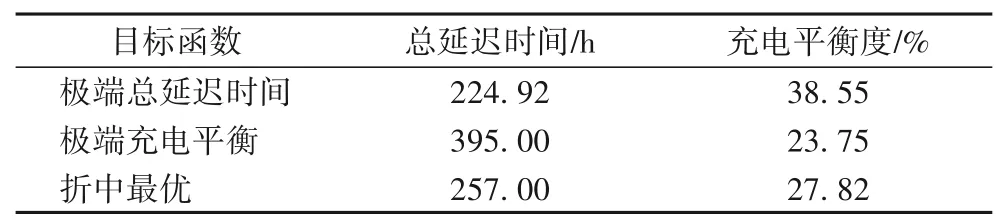
表3 系统极端解和折中最优解Tab.3 System extreme solution and optimal compromise solution
表4 给出GA 算法和改进NSGA-Ⅱ算法在最优折中解下的平均总延迟时间和平均充电平衡的结果。由表4 可知,相较于GA算法,改进NSGA-Ⅱ算法的折中解更优。

表4 两种算法实验结果对比Tab.4 Comparison of experimental results of two algorithms
3.4 结果分析
根据式(9)可知三相不平衡度的计算与N有关,因此在不同的N下,无序充电中的不平衡度值也不同。表5 给出无序充电和充电调度策略下折中最优解的结果,在本文充电调度策略下,EV 接入电网后负荷调度效果明显。与无序充电相比,在约束最严格时峰谷差、负荷方差、三相不平衡度和三相不平衡度方差分别下降56.54%、67.64%、69.23%、93.49%;而在约束最宽松的情形下(N=40 时,目标值为0)分别下降35.43%、53.99%、38.46%、47.47%。这表明与无序充电相比,该策略能够明显降低峰谷负荷差和三相负荷不平衡度,平抑负荷曲线波动,起到改善负荷特性的效果。
以类型1 中代表性的组合来说明该策略在降低负荷峰谷差的作用,图7 为无序充电和充电调度策略不同组合同时充电的车辆数。可知在无序充电下,大部分EV 集中在18:00—24:00 充电,加大了峰谷负荷值,不利于电网系统安全稳定运行。N=20 时,负荷削峰填谷效果非常明显。随着N的增加,峰值降低的程度随之下降,但与无序充电相比峰谷负荷差仍显著性降低。在N=40和Δ=0.2时,虽然峰值削减的力度没有其他组合的大,但避开电网负荷的高峰时段,使EV 负荷能在更长时间内分配,减小了对电网的冲击,从而更有效地平滑电网负荷波动。

表5 无序充电和充电调度策略下的指标对比Tab.5 Comparison of indexes under disorder charging and charging scheduling strategy
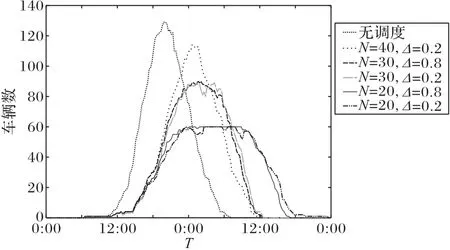
图7 无序充电和充电调度策略不同参数组合下的充电车辆数Fig.7 Numbers of charging vehicles under parameter of disorderly charging and charging scheduling strategy with different combinations
为进一步说明该充电策略对三相不平衡度的影响,根据不同N值以L1和L3的三相不平衡度来分析无序充电和调度策略。如图8 所示,在所有参数组合下,三相不平衡度基本低于0.2,且波动较小,利于电网的安全稳定。无序充电中三相不平衡度高达0.65,三相不平衡度值在整个时间范围内波动较大,影响配电网安全运行。而在采取调度策略后,三相不平衡度整体趋势较为平稳。随着N值的增加即约束更加宽松,三相不平衡度仍显著降低且波动不大。由此可见,将三相不平衡度作为一种约束,不仅对降低三相不平衡度有着重要意义,还使得三相负荷波动平稳,验证了该模型和策略的有效性。
为分析该充电策略对总延迟时间的影响,对静态和在线调度的48 种情形计算得到最优折中解下的平均总延迟时间,如表6 所示。从表6 中可看出,在折中最优解下,静态调度的总延迟时间要低于在线调度。另外,在静态调度类型1 中要找到总延迟时间为0的解是较容易的(N=40)。这是由于在线调度对EV 充电时间的分配受到实时限制,部分EV 的充电时段不能进行局部优化,得到不理想的充电时间。
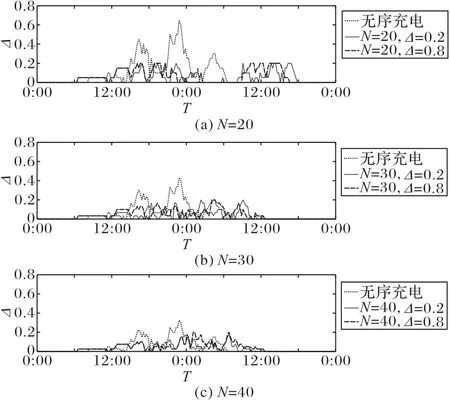
图8 无序充电和充电调度策略中不同N值的三相不平衡度Fig.8 Three-phase unbalance value under disorderly charging and charging scheduling strategy with different values of N
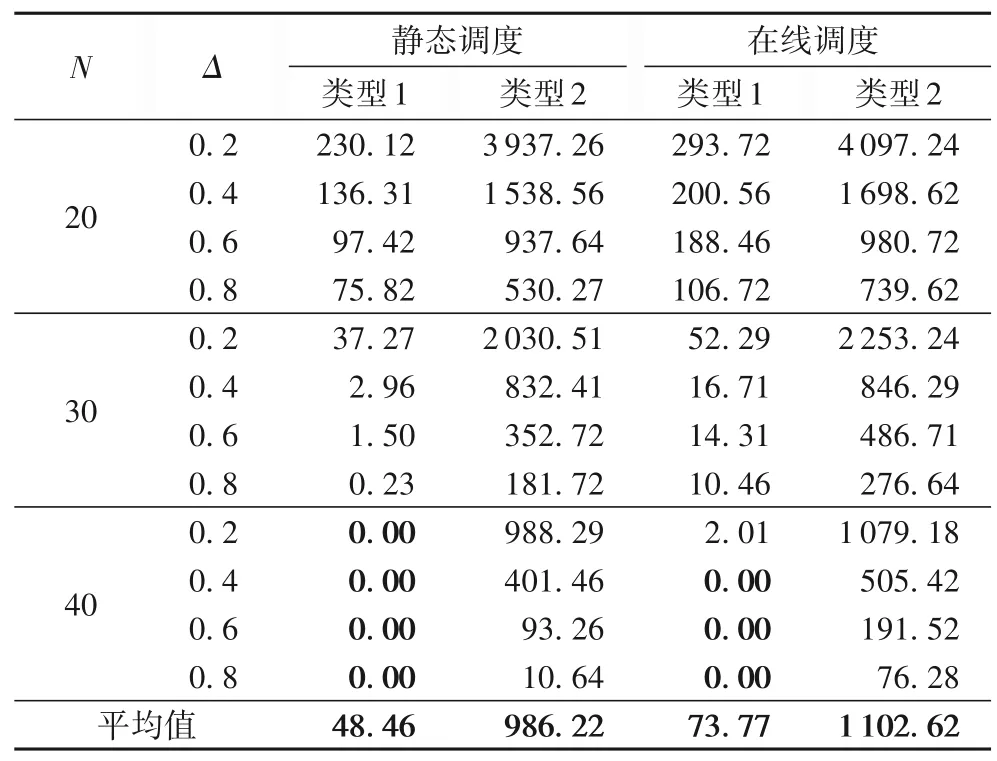
表6 静态和在线调度不同参数组合的平均总延迟时间 单位:hTab.6 Average total delay time of different parameter combinations of static and online scheduling unit:h
为进一步对EV不同到达类型进行分析,主要比较不同参数组合的平均总延迟时间。在每个参数组合下,类型1 中的总延迟时间要低于类型2,这是因为类型1中线路上的车辆分布是均匀的。而类型2 中车辆到达的差异非常大(L1为60%,L2为30%,L3为10%),由于三相不平衡限制使得总延迟时间的增加较为显著。
根据表6 可看出总延迟时间的大小取决于参数N和Δ的值,随着N和Δ值的减小即约束更加严格,总延迟时间会随之增加。在最极端的情况下,可参考在线调度类型2(N=20,Δ=0.2)的结果,车辆的平均延迟时间超过24 h。这主要是由于当L3中的18 辆EV 完成充电后,由于Δ=0.2 的限制,L1和L2中可同时充电的电动汽车数量值为4,使得L1和L2中的车辆充电时间出现巨大的延迟。这种极端的参数组合不能反映实际情况,但这些情况有助于测试调度算法管理极端情况的能力。该算法可以利用EV的到达时间、充电时间和期望离开时间的所有数据来获得较好的解决方案。
4 结语
本文提出一种兼顾负荷波动和三相不平衡的电动汽车多目标静态和在线调度充电策略,具有现实意义。采用改进NSGA-Ⅱ算法求解多目标问题,得到更加完整均匀的Pareto前沿面,并采用模糊隶属度函数得到折中最优解,避免了传统权重系数法对多目标优化的主观影响。实验结果表明,在不同约束组合下,该充电策略能够有效做到平抑负荷波动和实现三相平衡,并尽可能实现公平充电。随着可同时活动充电点数量和三相不平衡度值的减小,对于平抑负荷差和降低三相不平衡度的作用就越大,但总延迟时间也会随之增加,运营商可以根据实时情况进行选择,具有较好的参考意义。
另外静态调度中的目标值要优于在线调度,因此可以尽量获取到小区内车辆的数据,从而能够更好地解决在线调度问题。

