一种局部视角的类别近似质量属性约简加速方法
李智远 饶先胜 宋晶晶* 杨习贝
1(江苏师范大学科文学院 江苏 徐州 221116) 2(江苏科技大学计算机学院 江苏 镇江 212003)
0 引 言
属性约简,作为粗糙集理论研究的核心问题,不仅能有效降低数据的维度,且所得约简结果具有明确的语义解释,因而受到广泛的关注[1-7]。所谓属性约简,是指利用在某种度量标准上构造的约束条件,删除数据中冗余的属性,以提升后续学习算法的性能[8-9]。
在粗糙集理论中,近似质量[10]作为一种常用的度量标准,可以用于刻画样本空间的不确定性。具体而言,近似质量用下近似集合中的样本占所有样本比例的大小来表征不确定性的程度。近似质量的变化可以表现为下近似集合中样本数目的变化。以近似质量度量标准构造约束条件,采用前向贪心搜索算法,可以计算得到一个约简结果。值得注意的是,文献[11]指出,在求解约简的过程中,这一约简策略并未考虑到每一个决策类的下近似集合在约简前后的变化情况。也就是说,计算得到的约简并不一定会使得与每一个决策类的下近似有关的约束条件得到满足。因此,李智远等[11]从单个决策类的角度研究了这一问题,提出了类别近似质量和类别近似质量约简的定义,并设计了相应的算法来计算类别近似质量约简。
通过使用前向贪心搜索策略,求解类别近似质量约简,对于每个决策类,可以得到使其近似质量不发生降低的属性子集。与传统的近似质量约简求解的过程不同,求解类别近似质量约简,对于每个决策类会得到一个约简结果。值得注意的是,在利用前向贪心搜索策略求解类别近似质量约简的过程中,类别近似质量的计算是评估候选属性重要度必不可少的步骤,且在计算类别近似质量时,需要遍历论域中所有的样本,考虑样本的邻域与当前决策类之间的包含关系。显然,当面临的数据规模较大时,类别近似质量约简的求解会具有较高的时间消耗。然而,文献[12]和文献[13]指出,在计算某一决策类的下近似时,可以从局部的视角进行考虑,即仅考虑决策类中样本,决策类外的样本对于计算当前决策类的下近似并无帮助。因此,为降低求解约简的时间消耗,从局部视角出发,提出了一种求解类别近似质量约简的加速方法,借助于邻域粗糙集模型,设计了相应的约简求解加速算法,通过在约简求解的过程中减少计算规模,以加快类别近似质量约简求解的过程。
1 邻域粗糙集
经典粗糙集[14-15]由波兰学者Pawlak教授提出,是建立在严格的不可分辨关系[16]基础之上,适用于离散型数据。但在实际应用中,连续型数据广泛存在,当面向连续型数据时,经典粗糙集并不能直接对数据进行分析和处理,具有一定的局限性。为提高粗糙集模型的适用性,许多扩展的粗糙集模型被提出[17-21]。其中邻域粗糙集[17-18]由于能直接分析和处理连续型数据甚至与混合型数据,而受到广泛的关注[22-23]。
在邻域粗糙集中,一个决策系统可以表示为DS=
给定一个决策系统DS,对于论域U中的任意样本xi, 可以在某一距离度量标准上,通过给定的邻域半径,对样本xi的邻居进行考察,进而得出样本xi的邻域。值得注意的是,当给定的邻域半径过小时,容易导致样本的邻域仅包含其自身。为避免这一问题的出现,本文将采用邻域区间[18]的方式考察样本的邻居。∀xi∈U和∀A⊆AT, 给定一个邻域半径δ∈[0,1], 样本xi的邻域区间可表示为:
(1)
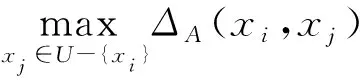
δA(xi)={xj∈U:ΔA(xi,xj)≤Int(xi)}
(2)
定义1[17]给定一个决策系统DS和邻域半径δ, ∀A⊆AT, 决策属性d关于条件属性集合A的下、上近似集为:
(3)
(4)
式中:Xp∈U/INDd。且:
(5)
(6)
定义2[18]给定一个决策系统DS和邻域半径δ,∀A⊆AT, 决策属性d关于条件属性集合A的近似质量为:
(7)
式中:|X|表示集合X的基数。
在条件属性集合A的基础上,定义2所示的近似质量表示了确定属于某一决策类的样本占所有样本的比例。因此,近似质量的大小可以用于刻画样本空间的不确定性程度。显然,γA(d)的值越大,样本空间的不确定性程度越低,且γA(d)∈[0,1]。
2 类别近似质量约简与加速方法
2.1 类别近似质量约简
根据定义2中的近似质量构造相应的约束条件,利用前向贪心搜索策略,可以计算得到一个近似质量约简。但值得注意的是,所得约简结果并不能保证约简后每一个决策类的近似质量得到保持或提升。因此,文献[11]在每个决策类别上单独进行考虑,提出了类别近似质量的概念,并给出了类别近似质量约简的定义。
定义3[11]给定一个决策系统DS和邻域半径δ, ∀A⊆AT和∀Xp∈U/INDd,类别Xp关于条件属性集合A的近似质量为:
(8)
定义4[11]给定一个决策系统DS和邻域半径δ, 对于决策类Xp∈U/INDd, ∀A⊆AT,A被称为一个类别近似质量约简当且仅当:
(1)γA(Xp)≥γAT(XP)。
(2) ∀B⊂A,γB(Xp)≤γAT(Xp)。
在定义4所示的类别近似质量约简描述中,约束条件(1)是用于寻找所有相关的属性,而约束条件(2)是为了确保所得约简中不包含冗余属性。值得注意的是,由定义4得到的类别近似质量约简是使得决策类XP的近似质量不发生降低的最小属性子集。在定义4所示的类别近似质量约简基础上,可进一步定义如下用于评估候选属性重要度的函数。
定义5[11]给定一个决策系统DS和邻域半径δ, 对于决策类Xp∈U/INDd, ∀A⊂AT,∀a∈AT-A,属性a相对于条件属性集合A关于类别近似质量的重要度为:
Sig(a,A,Xp)=γA∪{a}(XP)-γA(Xp)
(9)
式中:Sig(a,A,Xp)是用来描述当a加入到条件属性集合A中后,类别近似质量的变化情况。∀a∈A-AT, 若Sig(a,A,Xp)的值越大,则表明属性a对提升决策类Xp的近似质量作用越大,即属性a越重要。因此,可以将这一评估属性重要度的函数用于求解类别近似质量约简的前向贪心搜索算法中。
在使用前向贪心搜索算法求解类别近似质量约简时,会对候选属性的重要度进行评估,在每轮迭代的过程中,相对于当前约简集合具有最大重要度的候选属性会被选择并加入到当前约简集合中,直至满足所定义的约束条件。详细的过程如算法1所示。
算法1求解类别近似质量约简的前向贪心搜索算法
输入: 决策系统DS,邻域半径δ, 类别标记p。
输出: 一个类别近似质量约简A。
步骤1A←∅。
步骤2根据式(5)和式(8)计算γAT(Xp)和γA(Xp)。
//γφ(Xp)=-∞
WhileγA(Xp)<γAT(Xp) do
(1) ∀a∈AT-A, 根据式(5)、式(8)和式(9)计算属性重要度Sig(a,A,Xp);
(2)b=arg max{Sig(a,A,Xp) :a∈AT-A}
(3)A←A∪{b}, 并根据式(5)和式(8)计算γA(Xp)。
End While
步骤4输出类别近似质量约简A。
由算法1的过程可知,类别近似质量约简求解的主要时间消耗在于对候选属性的重要度进行评估,而类别近似质量的计算是评估属性重要度过程中必不可少的步骤。值得注意的是,计算决策类Xp的近似质量时,需要考虑论域中所有样本的邻域与决策类Xp之间包含关系。显然,当决策系统的样本规模较大时,类别近似质量约简的计算会具有较高的时间消耗。然而,文献[12]和文献[13]指出,在计算决策类的下近似时,可以从局部的视角进行考虑,即仅需要考虑当前决策类中样本的邻域与当前决策类之间包含关系,这是因为样本的邻域包含其自身,而当前决策类之外样本的邻域不可能包含于当前决策类,即不在当前决策类中的样本对于计算当前决策类的下近似并无帮助。因此,可以从局部的视角出发,通过减少计算规模,设计求解类别近似质量约简的加速方法,以降低计算约简的时间消耗。
2.2 类别近似质量约简求解的加速方法
给定一个决策系统DS和邻域半径δ, ∀A⊆AT,为加快计算Xp的下近似集合,可采用式(10)。
(10)
与式(5)不同的是,利用式(10)计算决策类Xp的下近似集合时,仅需考虑决策类Xp中样本的邻域与Xp之间的包含关系,无须遍历论域中所有的样本。此外,由上述的讨论可知,与式(5)相比,使用式(10)不会改变决策类Xp的下近似集合结果,但可能会具有相对较低的时间复杂度。因此,可以从局部视角出发,用式(10)来加快类别近似质量的计算,以降低求解类别近似质量约简的时间消耗。加速求解类别近似质量约简的详细过程如算法2所示。
算法2加速求解类别近似质量约简的前向贪心搜索算法
输入: 决策系统DS,邻域半径δ, 类别标记p。
输出: 一个类别近似质量约简A。
步骤1A←∅。
步骤2根据式(10)和式(8)计算γAT(Xp)和γA(Xp)。
//γφ(Xp)=-∞
WhileγA(Xp)<γAT(Xp) do
(1) ∀a∈AT-A, 根据式(10)、式(8)和式(9)计算属性重要度Sig(a,A,Xp)。
(2)b=arg max{Sig(a,A,Xp):a∈AT-A}
(3)A←A∪{b}, 并根据式(10)和式(8)计算γA(Xp)。
End While
步骤4输出类别近似质量约简A。
与算法1不同的是,在算法2计算类别近似质量的过程中,下近似集合的迭代更新使用的是式(10), 即在算法2中计算某一个决策类的下近似集合时,仅考虑当前决策类中的样本而不是论域中所有的样本。因此,使用算法2能减少属性搜索过程中的计算规模,进而可能会提高求解类别近似质量约简的时间效率。
3 实验与结果分析
为验证本文方法的有效性,选取了8组UCI数据集进行了实验,数据集的描述如表1所示。在实验中选择了10个邻域半径,它们的值为0.02,0.04,…,0.20。样本之间的距离度量使用的是欧氏距离。此外,在进行实验之前,对所有数据集的属性值进行了归一化处理。

表1 数据集描述
3.1 算法时间消耗的比较
分别使用算法1和算法2计算上述数据集的所有类别近似质量约简,并对算法求解所有类别近似质量约简的总时间消耗进行比较。详细的比较结果如图1所示。

(a) Amphetamines Consumption
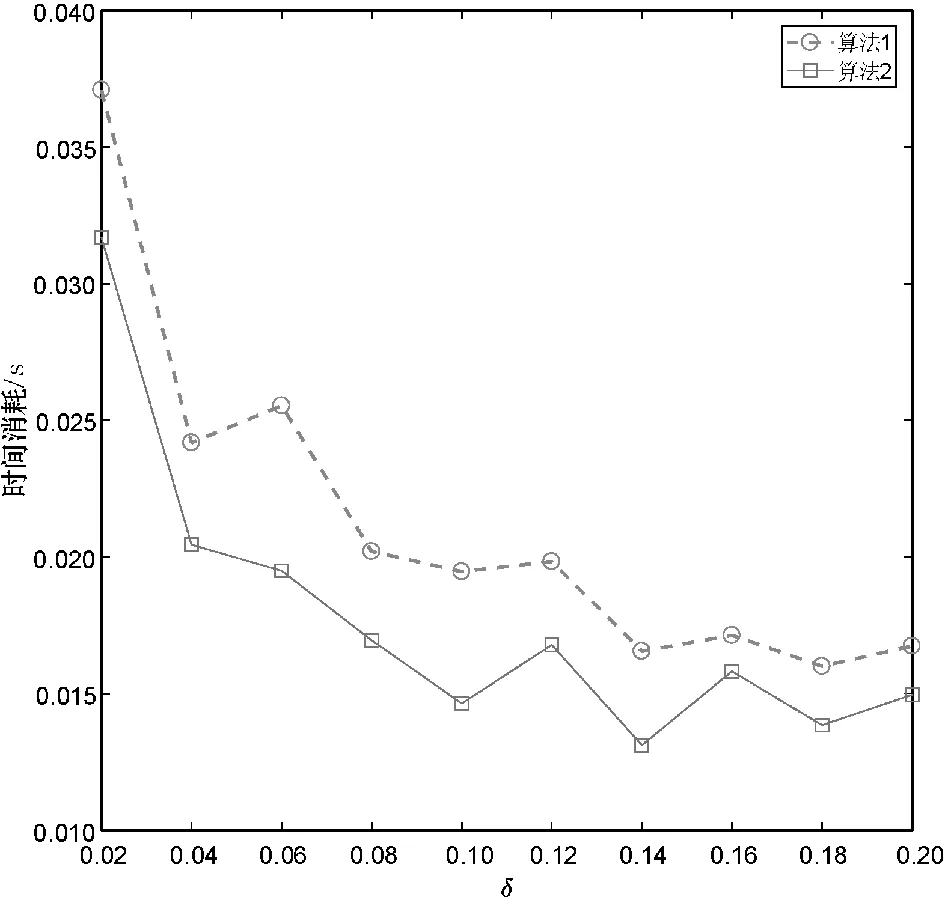
(b) Breast Tissue
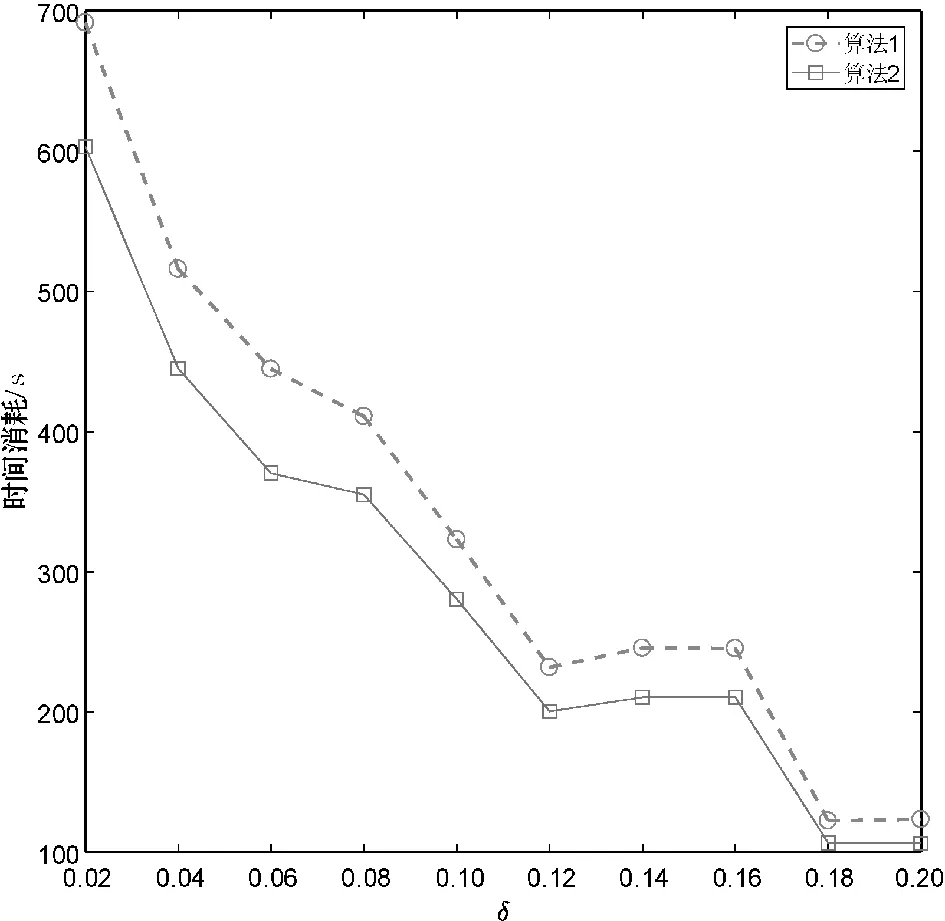
(c) Gesture Phase
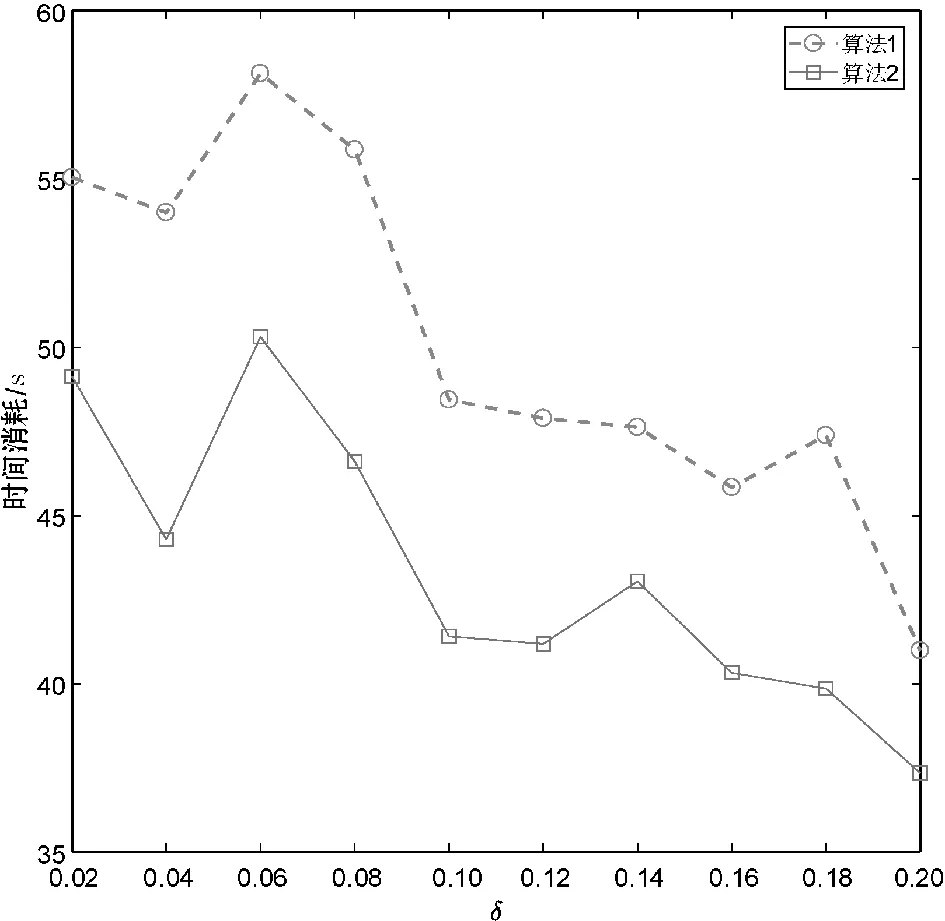
(d) Page-blocks

(e) Statlog (Heart)
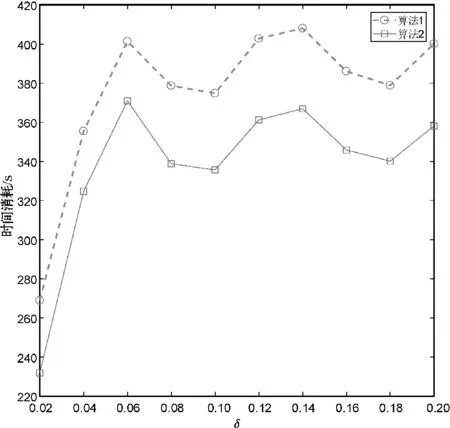
(f) Wall-Following Robot Navigation
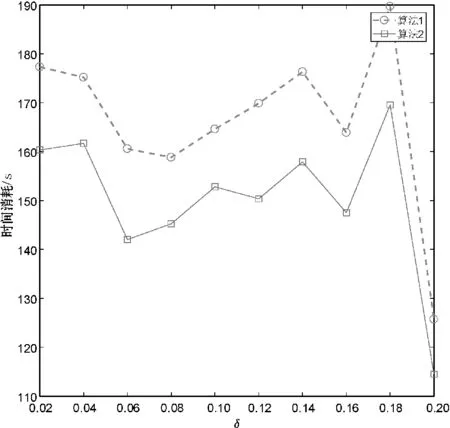
(g) Waveform Database Generator

(h) Wine Quality
观察图1不难发现,相较于算法1,使用算法2可以降低求解类别近似质量约简的时间消耗。这主要是因为在算法2求解约简的过程中,下近似集合的迭代更新是基于局部的视角,即计算某个决策类的下近似时,仅考虑了决策类中的样本而不是整个论域中的所有样本。由此可知,相较于算法1,第2节所提的加速方法有助于降低求解类别近似质量约简的时间消耗,进而提升约简求解的时间效率。
3.2 类别近似质量约简结果的比较
分别使用算法1和算法2求解类别近似质量约简,并对这两种算法计算得到的约简进行比较,详细的比较结果如表2所示。值得注意的是,为了简化实验结果展示和讨论,表2中仅比较了邻域半径为0.02和0.04时计算得到的约简结果。

表2 不同算法求解约简的结果比较

续表2
观察表2可知,相较于算法1,使用算法2求解类别近似质量约简并不会改变约简的结果。值得注意的是,在少数数据集上使用算法1和算法2 计算得到的类别近似质量约简中包含较少的属性。例如,考虑Wine Quality (序号: 8) 数据集和δ=0.02时,用算法1和算法2计算决策类X1的类别近似质量约简,所得约简中仅包含一个属性,这主要是因为,决策类X1中的样本相对较少,且利用全部属性计算的类别近似质量可能较小,这时,一个较少的属性子集可能就会满足约束条件,进而容易导致约简中包含相对较少的属性。
由图1和表2可知,与算法1相比,第2节所提的方法可以显著降低求解类别近似质量约简的时间消耗,且不会导致约简结果发生变化。
4 结 语
借助于邻域粗糙集模型,利用类别近似质量作为度量标准构造约束条件,通过前向贪心搜索策略,可以计算得到类别近似质量约简。但在约简求解的过程中,下近似集合的迭代更新需要考虑论域中所有样本的邻域与当前决策类之间的包含关系。显然,当面向的数据规模较大时,类别近似质量约简的求解会具有较高的时间消耗。鉴于此,从局部的视角出发,提出一种求解类别近似质量约简的加速方法。这一方法在更新决策类的下近似集合时,仅考虑当前决策类中样本的邻域与当前决策类之间的包含关系,进而可以减少约简求解过程中的计算规模,并提高计算类别近似质量约简的时间效率。此外,实验结果表明,与计算类别近似质量约简的未加速过程相比,本文方法在不改变约简结果的情况下,能有效降低计算类别近似质量约简的时间消耗。
在此基础上,下一步将从属性的角度进行考虑,并设计相应的加速策略进一步提高求解类别近似质量约简的时间效率。

