求解无约束优化的新子空间共轭梯度法
周国玲,曹名圆,杨月婷
(北华大学数学与统计学院,吉林 吉林 132013)
0 引 言
考虑无约束优化问题
minf(x),x∈n,
其中f(x)是n→上的连续可微函数.共轭梯度算法具有迭代格式简单、储存量小等优点,因而特别适用于求解大规模无约束优化问题,其基本迭代格式为
xk+1=xk+αkdk,k≥0,
(1)
这里的gk=∇f(xk)是f(x)在xk点的梯度,步长αk可通过精确线搜索方法或非精确线搜索方法求得,共轭参数βk-1的不同选取方式对应了不同的共轭梯度法[1-4].
Masoud Fatem[5]考虑用精确线搜索求解强凸二次函数极小时,线性共轭梯度法具有充分下降性、正交性以及共轭性等显著特性.利用式(1)构造如下关于共轭参数的一维优化模型
(2)
通过求解问题(2)确定共轭参数βk,这里的yk=gk+1-gk,sk=xk+1-xk.
另一方面,子空间技术因其可以减小计算成本和存储规模而被广泛关注[6-10].例如Stoer和Yuan[11]将二维子空间与共轭梯度法相结合提出了二维子空间极小化共轭梯度法,其搜索方向dk+1由当前梯度和最近一次搜索方向生成,即
dk+1=μk+1gk+1+νk+1sk,
其中μk+1和νk+1是标量参数.Yang等[12]提出一种子空间三项共轭梯度法,该方法在子空间Ωk={-gk+1,sk,sk-1}上构造目标函数的近似二次模型,再确定搜索方向.
受文献[5,12]启发,本文结合子空间技术,考虑算法的充分下降性和共轭性,构造一个带有惩罚参数的优化模型,通过极小化该模型确定搜索方向,进而提出新子空间共轭梯度法.
1 子空间共轭梯度法的提出
我们在二维子空间Ωk=span{-gk+1,sk}上构造如下优化问题
(3)
其中:d=-μgk+1+νsk是待定搜索方向,这里的μ、ν是待定参数;Mk为惩罚参数,当Mk较大时,增加搜索方向满足共轭性的机会,反之,搜索方向的下降性更强.将待定搜索方向d代入φk+1(d)得
这是关于μ、ν的二次函数,易见φk+1(d)关于μ、ν的Hessian阵
是半正定的.因此令φk+1(d)的梯度为0,即
(4)
则上式的解即为优化模型(3)的解.考虑以下3种情况:
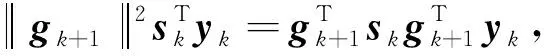
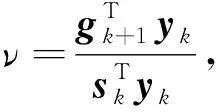
(5)
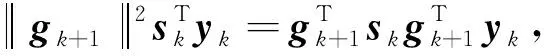
(6)
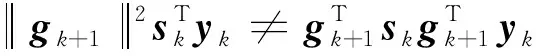
dk+1=-gk+1
(7)
由此,建立如下子空间共轭梯度算法.
算法1
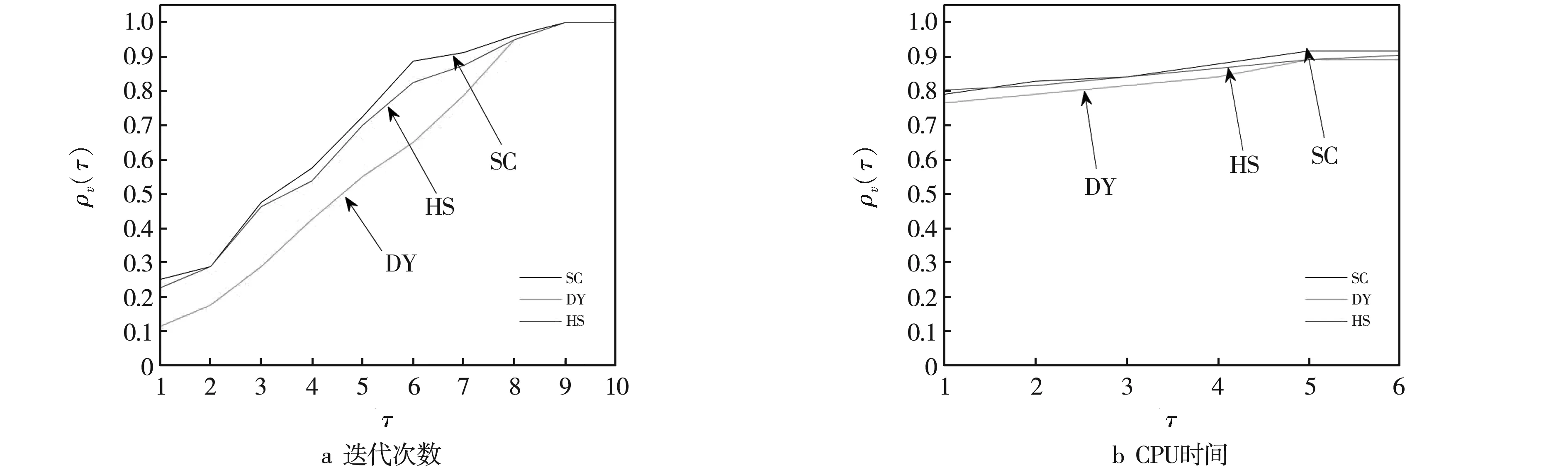
步0 给定初始点x0∈n,参数ε>0,0 步2 由Wolfe线搜索准则 计算步长αk. 下面证明搜索方向dk+1在不依赖任何线搜索的条件下,具有充分下降性. 证明:1)当dk+1由式(5)计算时,则 2)当dk+1由式(6)计算时,则 3)当dk+1由式(7)计算时,则 令c=1/2,引理得证.证毕. 本节证明算法1的全局收敛性.首先作如下假设: (H1)f(x)在水平集L0={x∈nf(x) 由假设(H1)~(H2)可知,存在一个常数Γ>0,使得 (8) 下面引理给出著名的Zoutendijk条件[13]. 引理3假设(H1)~(H2)成立,序列{xk}由算法1生成,如果 则 (9) 定理1假设(H1)~(H2)成立,序列{xk}由算法1生成,如果f是一致凸函数,即存在正常数γ使得 (10) 则式(9)成立. 证明:从假设(H2),有 (11) 又根据式(10)可得 (12) 1)当dk+1由式(5)计算时,可得 因此 2) 当dk+1由式(6)计算时,可得 因此 3) 当dk+1由式(7)计算时,可得 采用Dolan等[14]的评价准则,对算法1的迭代次数和CPU运行时间的性能进行评估,我们以迭代次数为例说明性能图上横纵坐标的物理意义.用τ>1表示最佳比值因子,用函数ρν(τ)表示某算法在迭代次数与所有算法中最小迭代次数的比值不超过τ时所求解问题个数占问题总数的比率,它反映了所测算法在迭代次数方面的性能.因此,本文对算法1(SC算法)、HS算法、DY算法,以τ为横坐标、ρν(τ)为纵坐标作图,图中曲线越高表明算法的数值性能越好.三个算法的性能评估结果如图1所示. 图1 算法性能对比Fig.1 Comparison of algorithm performance 从图1 a中可以看出,在迭代次数方面,算法1的性能曲线都在DY、HS的曲线之上,说明算法1在求解大规模无约束优化问题时能够使用更少的迭代次数,求解效率更高;图1 b表明算法1在CPU时间上也优于HS和DY方法. 本文研究了求解大规模无约束优化问题的新子空间共轭梯度法,且搜索方向满足充分下降性条件.在适当假设条件下,证明了算法的全局收敛性.数值结果表明,该算法在求解大规模无约束优化问题时具有较高效率,特别在迭代次数上明显优于HS和DY方法.
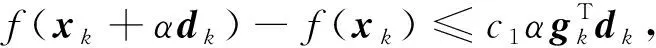
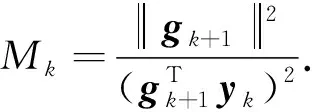

2 收敛性分析
3 数值实验
4 结 论

