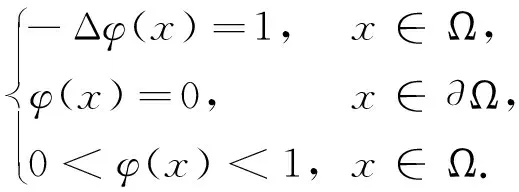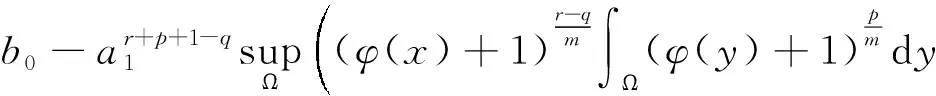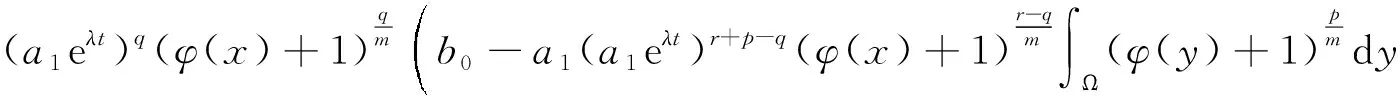具吸收项及非局部边界条件的多孔介质方程解的存在性和爆破
潘荣婷,高云柱
(北华大学数学与统计学院,吉林 吉林 132013)
0 引 言
本文考虑如下非局部初边值问题
(1)
方程(1)描述的是流体通过多孔介质的数学模型.许多物理现象被表述为非局部数学模型,包括不含吸收项的多孔介质模型[1-2],以及含有吸收项的多孔介质模型[3-7].
本文做如下假设:
(2)
本文研究了问题(1)的上解、整体解的存在性和解在有限时刻的爆破性.
1 预备知识
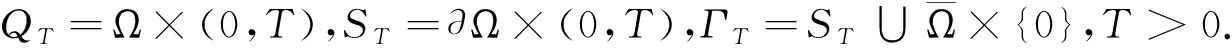
定义1称非负函数u是问题(1)在QT上的一个上解,如果u∈C2,1(QT)∩C(QT∪ΓT),并满足
(3)
类似地,若u≥0且满足式(3)不等号相反的顺序,则称u∈C2,1(QT)∩C(QT∪ΓT)是问题(1)的一个下解.如果u既是问题(1)在QT上的下解,也是问题(1)在QT上的上解,则称u是问题(1)在QT上的一个解.进一步地,对任意T>0,如果u是问题(1)在QT中的一个上解,则称u是问题(1)的一个整体解.

2 主要结果
定理1设l≤1,max{m,r+p}≤1 且假设(2)成立,则问题(1)存在上解.
证明:设T是任意正数.由假设(2)成立,我们在QT中构造问题(1)的一个正上解.对于l<1,只需取
则其为(1)的一个上解.
对于l=1 的情况,考虑如下的特征值问题
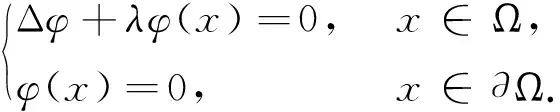
设λ1表示它的第一特征值,选择相应的特征函数φ满足(0<ε<1):
则不难得到

是问题(1)的一个上解.
事实上,由于
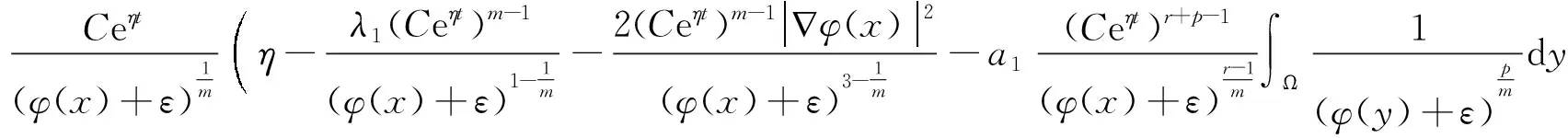
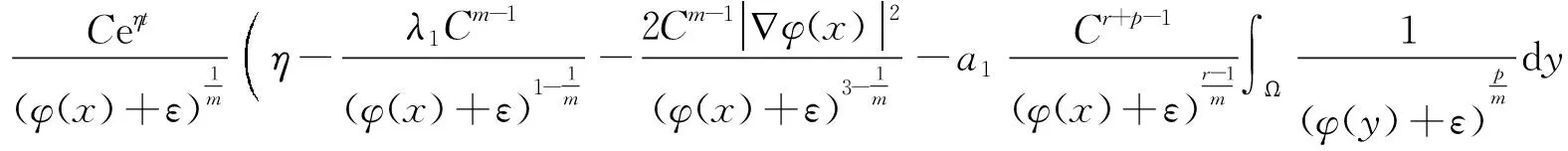
其中,

则易知v(x,t)是问题(1)在QT上的一个上解.证毕.
定理2设r+p>q,0 证明:设φ(x)是如下椭圆问题的解: 要使上式大于等于零,只需 (4) 进而 于是有 从而式(4)成立. 综上所述,取 考虑下列常微分方程 (5) 通过解上述简单的常微分方程,容易得到下面的引理: 引理2(ⅰ)如果r+p (ⅰ)如果1≤r+p 证明:考虑如下微分方程 (6) 显然方程(1)的解u(x,t)=v(t)是方程(6)的下解,而由引理2可得,v(t)是方程(6)的整体解,故由引理1比较原理即得证.证毕. 证明:考虑如下微分方程 (7) 显然方程(1)的解u(x,t)=v(t)是方程(7)的上解,而由引理2,方程(7)的解v(t)在有限时刻爆破,故由引理1比较原理即得证.证毕. 由引理2不难推得如下定理5: