教学平行四边形面积公式三环节

文|沈 强

平行四边形的面积计算容易受到长方形面积公式的负迁移和四边形活动框架拉伸的干扰，错误地认为平行四边形面积是邻边相乘。那怎么做能让学生更好理解其中的变与不变，可以采用以下的教学环节。

一、自主测量，产生认知冲突

1.自主测量，计算面积。

练习纸上呈现一个没有数据的平行四边形，让学生测量需要的数据，并计算面积。预设学生有两种答案（如图1），第一类学生是底乘高，第二类学生是邻边相乘。让学生说一说测量和思考的过程，对答案的正确性不作判断。

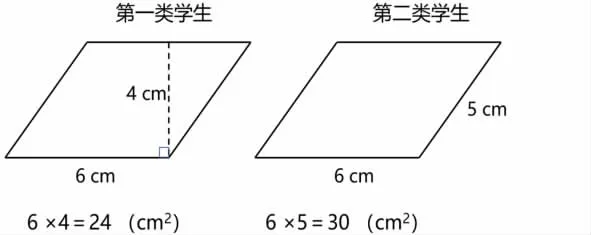
图1

2.对比分析，自主判断。

让学生在平行四边形旁画一个长6cm、宽5cm的长方形，并计算面积。将长方形与平行四边形的边线长度和面的大小进行对比，认为自己平行四边形面积算错的学生请举手示意。追问：现在你怎么知道自己算错了？学生独立思考后集体反馈。学生在表述时，呈现长方形与平行四边形的重叠图（如图2），通过割补将其转化为小长方形，与大长方形相比，面积相差上面的一部分。得出结论：平行四边形的面积用邻边相乘不正确。

图2

3.图形割补，变与不变。

思考：将平行四边形割补成长方形，什么没变？什么变了？面积没变，平行四边形割开后是两部分图形的面积之和，移动三角形部分到另一侧，两部分的面积之和没有发生变化。周长变了，让学生进行前后对比，上下两条边不变，由原来的斜边缩短成直角边，所以周长变短了。

二、回顾旧知，寻找问题起源

向第二类学生提问：你们当时怎么想到邻边相乘的？预设有两种学生，一种是受到长方形面积负迁移，另一种是受到四边形框架的干扰。呈现四边形活动框架，把活动框架从面积较小的平行四边形慢慢拉至长方形，让学生思考：在这个拉伸的过程中，什么变了？什么没变？发现四边形的面越来越大，所以面积变了。周长没变，因为一周的四条边只是移动了位置，长短没有变。再次验证：一般平行四边形面积用邻边相乘是错的。

三、自主整理，得出面积公式

呈现最初的平行四边形，面积怎么计算？为什么是底乘高？在学生交流中，用课件呈现割补的动画过程，寻找两者之间的对应关系，得出平行四边形的面积公式＝底×高。

呈现学生想法，暴露真实问题，自主进行辨析，寻找问题起源，得到面积公式，这是平行四边形面积公式第一课时所需要完成的任务。