在操作中理解 在审辩中内化——《图形的高与底》教学案例

文 董周涛 吕琼华

在学习《图形的高与底》之前，学生对三角形、平行四边形和梯形的特征有了一定的认识基础，对过直线外一点作已知直线的垂线有了一定的操作经验。基于此，本节课在设计时突出新旧知识之间的内在联系，重视对不同图形高的概念辨析，注重学生审辩思维能力的培养；同时期望学生在想象画高的过程中聚焦高的本质特征，为后续研究图形的面积积累经验。

【教学过程】

环节一：结合实例，唤醒“高”的生活经验。

1.谈话引入：生活中，哪里听说过“高”？

2.呈现实例：教师引导学生用“从……到……的距离”描述人的身高、楼房的高、大树的高等。

3.引出新课：（出示三角形、平行四边形、梯形）这三个之前学过的图形，它们有高吗？今天我们一起来研究图形的高与底。

【评析：在引入部分借助生活经验唤起学生对“高”的形象思维，以此过渡到图形的“高”，为后续学习提供生活经验和直观感知。】

环节二：初次探究，理解三角形高的概念。

1.猜想演示。

教师出示一个锐角三角形，学生基于经验猜想高的位置并演示用三角尺画高。师生交流三角尺的摆法和直角符号的使用，明确线段AO要与BC边垂直。（图1）

图1

2.概念辨析。

（1）阅读理解：教师呈现三角形的高与底的概念，引导学生阅读后说一说什么是三角形的高与底，同时结合概念判断线段AO是否为三角形ABC的高。

小结：从顶点A到垂足O的线段就是三角形ABC的高。

（2）深入辨析：将三角形ABC进行旋转，线段AO还是三角形的高吗？继续旋转呢？（图2）

生：我觉得不是高，因为高的位置变了，而且也没有垂直下来。

生：我不同意。虽然三角形旋转了，但是线段AO还是与BC边垂直的，所以高没有变。

生：我补充一下，刚才说高是顶点和垂足间的线段，现在顶点还是A，垂足还是O，所以线段AO还是BC边上的高。

3.自主画高。

（1）明确要求：想一想除了以BC边为底，三角形ABC还可以以哪条边为底作高？请你再选择一条边为底，画出底边上的高。

（2）呈现画法：画的是三角形ABC的高吗？为什么高的方向不一样？（图3）

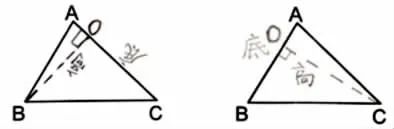
图3

引导：每一个顶点都能找到一条相对应的底边，也就能画出一条高，高和底有对应关系。

（3）检查纠错：这两条高都画对了吗？用三角尺检查一下。

4.启发想象。

师：刚才我们一起画了一条高，还画出了不同底边上的高。这个锐角三角形一共有几条不同的高？如果把三幅图重叠在一起，猜猜高会怎么样？

生：3条高会相交于一点。

师：这个交点会在哪里呢？

（学生用手指交点的位置，教师动画演示高相交于一点的过程）

【评析：展开“猜测—阅读—辨析—作高”四个步骤理解高的概念。猜测暴露学生原发的高概念；对照定义突出“高”概念的关键要素；跟进以变换图形的位置的辨析，概括出高的概念本质，从日常语言的“高”演化为数学概念的“高”；再次画高检查概念的生成情况，关注学生差异。】

环节三：再次探究，沟通三角形高的特点。

1.提出问题。

锐角三角形有3条高，那么直角三角形和钝角三角形呢？

2.动手操作。

教师出示活动建议（图4），学生自主探究直角三角形和钝角三角形中高的特点。如果感到画高有困难，也可以拿一张锦囊卡。（图5）

图4

图5

3.明晰画法。

教师依次呈现学生作品（图6），展开交流。

图6

师：这位同学的作业中，为什么直角三角形画了1条高，却写着有3条高？

生：因为另外2条高与2条直角边重合了。

（学生口述画法，教师演示将另外2条高画出来）

师：钝角三角形能画出几条高？（有学生画出1条，也有学生画出3条）除了这条高，还有2条在哪里呢？

教师请学生演示画出BC边上的高，并提问：为什么要先延长BC边？

生：如果不延长BC边，就不能确定垂足在哪里，就无法确定BC边上的高。

师：在画钝角三角形的高时要注意根据顶点的位置判断是否需要延长底边。

4.交流发现。

师：刚才我们一直在研究三角形的高，你发现了什么？

生：我发现三角形都有3条高。

生：锐角三角形的高都在三角形的里面，直角三角形有2条高就是它的直角边，钝角三角形有2条高在三角形的外面。

生：我发现锐角三角形和直角三角形的高都有一个交点，而钝角三角形的3条高没有交点。

生：我觉得钝角三角形的高可能也有交点。

师：钝角三角形的三条高从图上看好像没有交点，但是如果我们把高延长呢？（教师动画演示，图7）

图7

师：在三角形ABC中，保留BC边，去掉另2条边，你有什么发现？（图8）

图8

生：三角形的高就是点到直线的距离。

师：没错！想象以BC为底，AO为高还可以画出哪些图形？

生：长方形、平行四边形、梯形……

【评析：特殊三角形的高是学习的难点，因此教师先从锐角三角形入手构建高的概念，再过渡到直角三角形和钝角三角形的高。通过解决“锐角三角形有3条高，直角三角形和钝角三角形呢？”这个问题，引导学生通过画一画、判一判等活动，以数学概念为依据，进行判断和操作，进一步巩固了高的概念，发现了三角形3条高相交于一点的现象，又解决了在作高过程中需要延长底边等难点。】

环节四：类比迁移，探究平行四边形和梯形的高。

1.尝试画高。

学生尝试画平行四边形和梯形的高，教师巡视指导。画好后组内学生交流画法及发现。

2.概念辨析。

（1）教师呈现两类典型情况（图9），分别请学生说明理由。

图9

生1：我根据三角形的高想到了从平行四边形的4个顶点出发来画高，画了4条。

生2：我觉得从平行四边形的AD边上任选一点都可以向对边画高，因为这些高都相等。

师：你们同意谁的观点？（大部分学生同意生2）到底可不可以这样画呢？

学生阅读平行四边形高与底的概念，交流明确：从平行四边形一条边上的一点向对边作一条垂线，这个点和垂足间的线段叫作平行四边形的高。师生依据概念演示画高。

（2）想象：这样的高有几条？你联想到了什么？

生：这条边上有无数个点，每个点都可以向对边画高，所以有无数条高。

生：我发现平行四边形的高就是两条平行线之间的距离。

师：数学知识之间有着紧密的联系。刚才还有同学画了这样的高，你觉得可以吗？像这样的高又可以画几条呢？（图10）

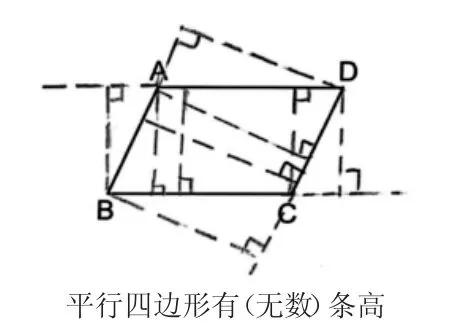
图10

（3）师生交流梯形的高及其特点，借助错例理解概念。

3.沟通比较。

师：通过刚才的研究，你发现平行四边形和梯形的高有什么相同点？又有什么区别？

生：它们都有无数条高。

生：平行四边形有2组对边，所以有2组不同的底和高，而梯形只有1组对应的底和高。

生：梯形的2条腰不平行，是不能作为底来作高的。

生：我还发现平行四边形和梯形的高就是平行线间的距离。

【评析：三角形、平行四边形和梯形的高本质上是相通的，因此本节课借助学习三角形的高的经验为学习平行四边形和梯形的高的学习做铺垫，在操作、比较、辨析、辩论的活动中自主探究平行四边形和梯形的高，更进一步地发现高与点到直线的距离、平行线之间的距离之间的关系，构建更加完整的数学认知体系。】

环节五：对比总结，聚焦图形之间高的联系。

师：今天我们研究了什么？三角形、平行四边形、梯形的高有什么区别和联系？

生：高的数量不同：三角形只有3条高，平行四边形和梯形有无数条高。

生：三角形的高就是点到直线的距离；平行四边形、梯形的高是平行线间的距离，所以有无数条。

生：如果先确定了一个点，其实平行四边形和梯形的高与三角形的高一样都是点到直线的距离。

师：你们不仅能通过对比发现区别，还能透过表面抓住本质的联系。在后续学习中，我们还会继续研究图形中高的作用。（图11）

图11

【评析：教师着重从两方面引领学生学习：一是通过变式、辨析和辩论，围绕概念关键要素展开学习活动，在操作和审辩中突出“点”“对边”“垂线”“垂足”等要素，突破难点，建构概念。二是深入知识本质进行沟通和关联，帮助学生不断完善认知结构。从三角形的高过渡到平行四边形和梯形的高，然后梳理出不同图形高的相同点和不同点，最后将高抽象为点到直线的距离，高的本质特征愈来愈明晰，高的概念越来越概括化、结构化，空间观念得到了培养和发展。】