错误中寻找问题对比中明晰概念——分数意义错例分析的诊断式教学策略

文|符玲利

一、平衡教学，完善分数概念

【错例呈现】把4米长的绳子剪成相等的3段，每段长（）米，每段是全长的（）。

【成因分析】

每段长度是多少求的是平均分的结果，当结果不能用整数表示时可用分数表示。每段是全长的几分之几求的是一段与整条绳子之间的关系，学生分不清分数的两种意义，故出现各种错误。

分数的意义主要有：比和数。关于“比”，小学阶段主要让学生理解部分占整体的比率，部分占部分的比率。“数”表示的是某对象的大小，常称为量。两者不同的含义需要在等分除与包含除不同的情境下去理解。

教学中我们习惯用等分除代替包含除来理解一个数是另一个数的几分之几。如在三年级《分数的初步认识》一课中，教材呈现的是把一个月饼平均分成2块，一块月饼是整体的二分之一，我们也常常按教材编排的逻辑进行教学。但其实这里存在两个概念，一是把一个月饼平均分成2份，每份是个月饼，这是等分的结果；二是这个月饼共分成2份，即1个月饼里包含2个个月饼，个月饼占整个月饼的，这是求部分与整体的关系。后者与倍的认识原理相同，都是求一个量里包含有标准量的几份或几分之几，没有了包含除的体验，“率”的理解就存在缺失。

【教学策略】

1.先“量”后“率”，同步建构。

教材在编排上倾向于等分除，但教师在教学的过程中可以适当平衡，如三年级《分数的初步认识》可分为2课时教学，第一课时让学生理解一个月饼平均分成2份，每一份的大小是块，引导学生充分感知在等分的结果不够1时，可以用分数来表示。此时的分数比1小，比0大，它有大小，在数轴上可找到它，它的出现让数学体系变得更丰富。第二课时可以利用包含除进行教学，如1个月饼里有2个块月饼，块月饼占整个月饼的关系可以用分数来表示，块月饼是整个月饼的个西瓜是整个西瓜的再设计直观长方形图（如下图），涂色部分占整个长方形的几分之几？你是怎么知道的？通过操作，学生理解需要先知道整体里包含有几个这样的一份，才能知道它占整体的几分之一，这样，学生既理解了部分与整体的关系，又能理解分数是度量的结果，丰富了其对分数作为“率”的认知。

2.“量”“率”并行，对比建模。

五年级分数的意义内容丰富并且抽象，教学时需要让学生理解分的对象既可以是离散的量，也可以是连续的量（如米、吨）。还需要让学生对平均分这一过程有新的认知，从大小、形状的平均分逐步抽象到量的平均分。最主要的是要让学生关注到分的两种不同结果及其表示的不同含义。当将单位“1”进行等分时，等分的结果是一个量，可以用整数或分数来表示。分数表示一个具体数量的数时，与整数一样，也有大小、意义。从包含除的角度思考部分与整体的关系也可以用分数来表示。量与率的同步教学、对比建模让学生清晰地感受到了分数的两种不同属性。

二、多重对比，理清量率关系

【错例呈现】

A.小明 B.小红

C.一样多 D.无法判断

学生常见错误：不懂两者区别，不能进行有效分析，随意填结果。

【成因分析】

人教版教材第一学段《分数的初步认识》侧重从部分与整体的关系理解分数意义，即“率”；第二学段《分数与除法》侧重引导学生理解等分的结果是一个量，可用分数表示。两个内容独立安排教学，且教材始终没有安排两者之间的比较，直到复习（练习二十）中才安排两者同时出现（如下图），对比练习的缺乏容易造成学生对概念中的相似意义混淆不清。

1.把一根2m长的木条锯成同样长的4段，每段是这根木条的（）（），每段长（）÷（）=（）m=（）（）m。

【教学策略】

1.题组对比，加深理解。

小学里分数的学习主要有两个阶段，在不同的阶段里均要安排量与率的对比。三年级主要是离散量中找分数，量和率会有明显区别。比如，苹果有6个，取出它的几分之几。取出——2个；取出——4个；全部取出即（也就是1）——6个。通过操作学生发现每一个量对应的都有一个率，从而感知量与率的区别。

五年级则出现了“米”“吨”这些计量单位，连续量的出现让量和率的理解更抽象。用题组对比方式呈现，借助图形直观，能够加深学生对量与率的理解。

如把6米长的绳子平均分成3段，每段长6÷3=2（米），每段是全长的

把3米长的绳子平均分成3段，每段长3÷3=1（米），每段是全长的

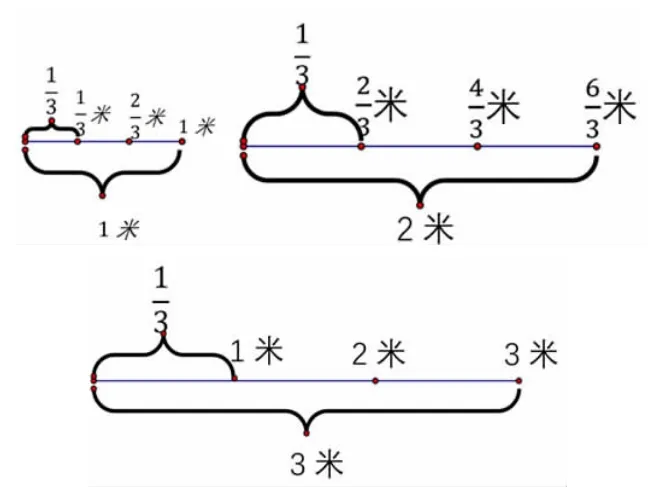
这样的题组呈现有利于学生对比发现：每段长度=总长度÷段数（3），总长度（具体量）发生改变，每段的长度也会发生改变。虽然每段长度不同，但每段占全长的不变，因为都是将全长平均分成3段，全长包含有这样的3段，故1段占全长3段的

2.变量对比，凸显差异。

如何让学生区分量与率的不同？最直接的方式是将两者摆在一起对比，通过改变其中的一个量，体会量与率的可变性与不变性。如研究一根绳的米的大小关系，要考虑绳子的长度，将绳长分类再对比，体会米的变与不变。

（3）如果绳子的长度小于1米，例如绳子长0.8米或0.75米，则其绳长的米。

三、多元表征，疏通前后联系

【错例呈现】

学生常见错误：题1中，甲、乙的大小判断无从下手，或是只判断的大小。题2中，女生是男生人数的几分之几一般用减法算出

【成因分析】

两题的错误均因为学生找不准单位“1”，无法理解单位“1”的可变性。

【教学策略】

1.数形结合，从部分与整体的角度体会单位“1”的可变性。

教学时教师可适当地丰富素材，呈现大小不同、形状不同的图形，让学生找出各个图形的，同时找每幅图中谁是谁的二分之一，这样的活动既可以让学生发现共性：只要把一个物体等分成2份，每份就是它的。又可以发现区别：单位“1”不同，得到的块的大小、形状也是不同的。

2.前后梳理，在两个量的对比中感悟单位“1”的转换。

部分与部分的关系教学可结合倍的知识进行，利用旧知迁移解决问题。如人教版教材呈现的是7只鹅、10只鸭、20只鸡，适当将数据改编成5只鹅、10只鸭、20只鸡，学生可以在复习中回忆两个量的倍数关系：鸡的数量是鸭的2倍，鸡的数量是鹅的4倍，同时体会因标准量的可变性导致相应的倍数变化。在此基础上提出鸭是鸡的几分之几呢？鹅是鸡的几分之几？学生顺势将知识、经验进行迁移，产生关键问题：标准量是什么？怎么去找它们之间的关系？

教师可以借助图形，帮助学生利用图形直观理解部分与部分的关系。