蓄力创生 厚植思想——《集合》教学实践与思考

文 夏向阳 张磊铭

【教材分析】

集合是现代数学的基本语言，可以简洁、准确地表达数学内容。集合思想是数学中最基本的思想，甚至可以说集合理论是数学的基础。学生从一年级学习数学时，就开始接触集合的思想方法，具备了一定的认知经验和知识技能。人教版教材在三年级上册安排了教学集合思想的单元，介绍了维恩图表示集合及交集、并集的方法，让学生体会集合的概念及认识集合的交集、并集，学习用集合的思想方法思考和解决简单的实际问题，为今后学习相关内容奠定扎实基础。

【教学过程】

一、设疑导入，激活认知经验

师：校运动会到了，三（1）班报名参加男生60米短跑比赛的有5人，男生100米短跑比赛的有4人。你觉得参加这两项短跑比赛的男生一共有几人？

生：9人。

师：除了9人，还有其他的可能吗？

生：还有可能是8人。因为有1名男生同时参加了这两项比赛。

师：谁听懂了他的意思？

生：有1名男生既参加了60米短跑比赛，又参加了100米短跑比赛。

师：你真会思考，值得表扬。

师：除了9人、8人之外，你们觉得还有其他可能吗？

生：7人、6人、5人。

师：7人、6人、5人又是怎样的情形，等会儿我们继续讨论。

【设计意图：以学生喜闻乐见的校运动会短跑比赛为教学情境，激活学生的认知冲突，初步感知生活中的集合现象，激发学生进一步探究的内驱力。】

二、聚焦本质，建构数学模型

1.自主探索，引出集合。

师：如果有8人参加比赛，请你思考怎样的情况才能保证有5人参加60米短跑比赛，4人参加100米短跑比赛？

师：接下来请同学们用自己喜欢的方法表示出8人的情形。

师：大家看懂了吗？

生：有1个男生参加了60米短跑和100米短跑两个项目，并用文字加以说明，再写上一共8人。

师：涂阴影的这两个圆表示什么意思？

生：表示同一个人参加了这两项短跑比赛。

师：下面我们来看这位同学的表示方法，她也是采用画图的方式。

师：这位同学的方法，你们看得懂吗？

生：看得懂，中间的这一位同学参加了两项比赛，这样一共有8人。

师：你们觉得刚才两位同学表示的方法有什么不同？

生：第一种方法同一位男生画了两个圆表示，然后用文字加以说明；第二位同学的方法把同一位男生只画了一个圆来表示。

生：第二种方法还画了两个相交的椭圆，这样看起来更加清晰。

师：我们再来看一位同学的方法。

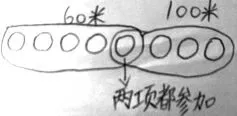
生：这位同学的方法和第二位同学的方法差不多，第二位同学画的两个椭圆是上、下顺序，而这位同学画的两个椭圆是左、右顺序。

生：这位同学画得更美观，看起来更方便。

师：三位同学通过画图的方法，把参加两项比赛的8人清晰地表示出来，像这样的图示法，数学上称为“维恩图”，由英国著名逻辑学家维恩第一个用这样的图来表示，所以称为维恩图。维恩图又叫集合图，今天这节课我们就来学习“集合”的相关知识。

【设计意图：教师给予学生充足的时间和空间，让学生用自己喜欢的方法进行表示。通过依次呈现学生原生态的作品，在象形图的基础上，进行不断加工、改造，顺利地经历维恩图的生成过程，从而丰富学生对维恩图的认识，获得有价值的数学活动经验，并通过不断比较和优化感受数学的简洁和美观。】

2.介绍集合，理解含义。

师：请同学们结合这幅维恩图继续思考，每一部分分别表示什么意思？

生：左边的椭圆表示的是参加60米短跑这一项的人数，相交部分表示的是两项都参加的人数，右边的椭圆表示的是参加100米短跑这一项的人数。

师：那左边的四个小圆又表示什么意思呢？

生：只参加60米短跑的人数。

师：那右边三个小圆和中间的这个小圆又表示什么意思呢？

生：右边三个小圆表示只参加100米短跑的人数，中间的这个小圆表示参加两项比赛的人数。

师：为了更加清晰和完整，我们把刚才维恩图中的每一部分所表示的意义在同一幅图上依次表示出来。

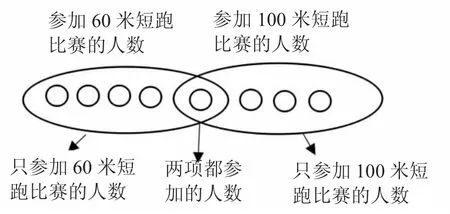
【设计意图：借助维恩图这一形象的表征方式，使学生深入感知维恩图的结构以及每一部分所表示的意义。在对比教学中深刻理解集合的概念，并能整体把握维恩图的互异性和无序性的特征，初步体会交集、并集的意义。】

3.列式解答，探究方法。

师：根据维恩图，你能用一个算式进行解答吗？

生：5+4-1=8（人）。

师：为什么还要减去1呢？

生：因为有1人重复算了。

师：是的。5+4我们把其中的一位同学算了几次？实际上呢？所以为什么要减1呢？

生：把重复算的这1次减去。

师：说得真好，我们能否结合算式在维恩图上指出来？

生：4+3+1=8（人）。

师：这个算式，谁能说一说它表示什么意思？

生：把只参加60米短跑和只参加100米短跑的学生相加，再加上两项都参加的学生。

【设计意图：鼓励学生从不同角度观察维恩图，列出不同的算式，并对照维恩图解释所列算式，渗透算法多样化的思想。】

4.拓展提升，发散思维。

（1）抽象成数。

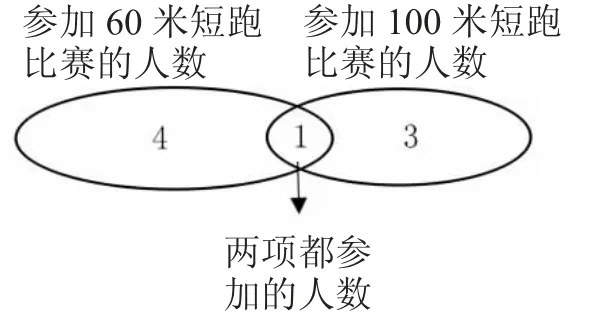
（2）完善集合。

师：除了9人、8人，还有其他的可能吗？

生：7人。

生：6人。

生：5人。

师：我们先用维恩图表示7人的情况。

师：请你观察，为什么参加60米和100米短跑的同学一共有7人？

生：2人同时参加了两项比赛。

师：为什么参加两项比赛的是6人？这又是什么道理？

生：有3人两项比赛都参加了。

师：刚才有同学说到5人，那5人的情况你能画出来吗？尝试在纸上画一画。

师：同学们，请你结合图进行思考，为什么参加两项比赛的人数是5人？

生：4人两项比赛都参加了。

师：右边空的部分表示什么意思？

生：没有人只参加了100米短跑比赛。

师：也就是说参加100米短跑比赛的同学都参加了60米短跑比赛。同学们，既然这儿没有人，那我们也可以把图变一变。

师：外面的椭圆表示什么意思？里面的椭圆表示什么意思？这个小圆又表示什么意思？

生：外面的椭圆表示参加这两项比赛一共有5人，里面的椭圆表示参加这两项比赛的有4人，左边的这个小圆表示只参加60米短跑的有1人。

师：同学们，那参加的人数一共是4人，有可能吗？

生：不可能，因为参加60米短跑比赛的就有5人了，所以参加比赛的至少有5人。

师：刚才我们通过“参加这两项短跑比赛的男生一共有几人”这一问题，借助维恩图和算式表示出了所有可能的情况，用维恩图来解决问题的思想在数学上叫做集合思想。

【设计意图：由形抽象到数，使学生完成数学化的过程，形成抽象的数学认知结构。同时，在不断思考、多次表征这一问题的不同情况下加强学生的认知经验，系统认识集合中相交、包含、相离三种关系，进而对集合形成正确、完整、深刻的认识。】

三、回顾总结，适时交流反思

师：通过今天这节课，你有什么收获？

【教学思考】

一、学习材料和认知经验是创生的引擎

本课中笔者巧用教学素材，让简单的素材尽可能发挥出最大的教学效果。以学生生活中的校运动会为情境，始终围绕“参加这两项短跑比赛的男生一共有几人”这一核心问题展开教学，思路清晰，指向明确，引导学生重点掌握有重叠部分的相交关系，同时对其他情况进行有序思考，探索出集合中相交、包含、相离三种关系，建立了对集合关系的系统认知，实现了数学思维的拓展。同时，唤醒“重复的人数要减去”这一熟悉的认知经验，运用学生的生成素材，放手让学生自主表征，利用学生生成的资料展开交流，不断完善，逐渐“创造”出维恩图。做到学为中心，素养为先，使学生真正参与到课堂中，让课堂的生成散发思维的火花。

二、思想方法和数学模型是创生的内核

本课在探究集合模型时，以学生原生态的表征为基础，启发引导、分享质疑、完善思考。从最初的两个圆涂阴影表示重叠的学生到一个圆放中间表示这位学生，探索出维恩图的雏形，再到圈一圈、移一移等方式优化维恩图，学生在思维活动中经历了较为完整的维恩图形成过程，在自主探索和教师引导下不断优化，使原本复杂、抽象的知识具体化、可视化、简洁化，无形中渗透着集合思想、优化思想、分类思想和数形结合思想，建立了集合问题的基本模型，培养了学生的思维能力，提升了学生的数学核心素养。