问题驱动，凸显数学本质——《用字母表示数》教学设计

文|万小丽

【教学内容】

苏教版五年级上册第99、100页。

【教学过程】

一、创设情境，初步感知

（课件出示动物园里小动物跳格子的游戏）

师：瞧，第一个出场的是小松鼠，它跳了几格？

生：13格。

师：小松鼠还想继续练习，猜一猜，它可能跳几格？

生1：它可能跳40格。

生2：它也可能跳35格。

生3：这里有50格，它可能跳1~50之间任意的格数。

师：能确定到底跳几格吗？

（学生摇摇头）

师：刚才我们知道是几，可以用具体的数来表示。现在不能确定到底是几，可以想个什么办法表示出所有可能的数？

（学生小组内交流）

生1：我们组用□来表示，□里可以填任何一个数。

生2：我们组是用x表示，因为x就表示未知数。

生3：我们组用n来表示,因为n可以表示任意数。

生4：是的，我妈妈经常说“这个问题已经遇到n次了”。

师：同学们真厉害，都想到了用简洁的符号来表示所有可能的数。在图形符号和字母之间，你更喜欢哪一种？

生：我觉得用字母来表示更简洁、更方便。

师：除了大家说的n、x之外，其他字母可以吗？

生：26个字母都可以。

师：那我选用a来表示，这里的a可以是哪些数？

生：a是1~50之间的数，因为这里只有50格。

师：字母可以表示任意数，但在具体的情境中表示一定范围内的数。

【设计意图：“用字母表示数”是学生代数知识的起点，创设“小松鼠跳格子”游戏，巧妙地将学生置身于问题情境中，经历从已知到未知的过渡。已知情况用数来表示，学生已积累丰富的经验，但对“未知情况怎么表示”学生第一次接触。通过小组交流，学生打破以往的固化思维，主动联系已有知识和生活经验，联想到用简洁的符号表示未知数，初步感受符号的优越性，然后结合“跳格子”的实际情境，理解字母表示的是一定范围内的数。】

二、比较辨析，深化理解

1.用字母表示数。

（课件出示小青蛙出场的画面）

师：小青蛙出场了，它会跳几格？

生1：青蛙跳b格。

生2：青蛙跳c格。

生3：26个字母都可以表示。

生4：我不同意，刚才说小松鼠跳a格了，这里就不能用a表示。

师：为什么不能用a表示？

生：还用a就重复了。

生：用a就说明青蛙和松鼠跳得同样多，可是它们跳得并不一定同样多，所以还是用不同的字母表示比较合理。

师：大家认可谁的想法？

生：除a之外的25个字母都可以。

师：同学们考虑问题很全面！同一个问题中，不同的数量通常用不同的字母表示。

2.用字母和数进行运算。

（出示：青蛙比松鼠多跳8格。青蛙跳几格？）

生：松鼠跳了a格，青蛙比它多跳8格，就用a+8表示。

师：刚才说青蛙跳b格，现在又用a+8表示。比一比，你认为选择哪个更合适？

生1：我觉得a+8更合适，因为它已经告诉我们青蛙比松鼠多跳8格。

生2：我觉得b好，比较简洁。

生3：我不同意他的观点，这里用b表示看不出青蛙比松鼠多跳8格，所以用a+8更好。

一是经费保障。职业教育的教育教学方式和教育对象决定了其高投入、高成本、低收费的特征。要完善市、区县两级财政分摊机制，保障对职业教育发展的长效稳定投入。区县政府要加大财政支持力度，积极落实职业学校生均公用经费，达到或超过国家和市里要求；落实兼职教师工资福利，保障教职工绩效达到基础教育学校水平；落实建设维修等经费，保障职业教育教学正常运行。

师：是的，当两个数量之间有关系时，一个数量用字母表示，就可以根据数量关系写出含有字母的式子来表示另一个数量。让我们再来体会这样的关系。

师：如果a是5，青蛙跳几格？如果a是10，a是22……

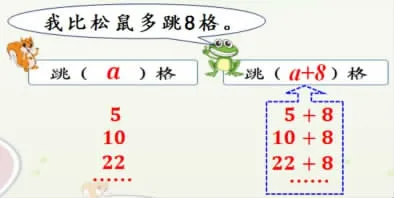
师：仔细观察这些数和算式，你有什么发现？

生1：当a变化时，a+8的结果也随之变化。

生2：a是变化的数，但是加8没有变。

师：变中有不变。这些不同的算式都可以用哪个式子概括出来？

生：都可以用a+8来表示。

师：看来a+8真的有魔力，通过这个式子你还能看出什么？

生：我还能看出青蛙比松鼠多跳8格。

师：如果青蛙跳a-4格，你又看出什么？

生：青蛙比松鼠少跳4格。

师：a×3呢？

生：青蛙跳的格数是松鼠的3倍。

师：这些含有字母的式子不仅表示青蛙跳的格数，还能看出数量之间的关系。

3.理清关系写字母式。

师：终于到小兔子登场了。小兔子比青蛙少跳两格。它跳几格？

生1：a+8-2。

生2：a+6。

师：这两个式子比一比，你会选择哪个？

生：a+6更简洁，而且能知道它们之间的关系。

师：从a+6还能看出什么？

生：兔子比松鼠多跳6格。

【设计意图：通过“青蛙跳的格数”的表达方式，首先让学生体会到“同一问题中，用不同的字母表示不同的对象”；接着赋予几个数量之间的关系，让学生经历用字母和数一起运算写出字母式的过程。用字母表示数的真正价值在于字母能和数一起进行运算，这里让学生自己去发现这个规律，在此过程中对两种表达方式进行比较，学生通过一番争辩达成了共识，逐步理解含有字母的式子既表示结果也表示关系。赋予字母具体的数值，学生体会到当字母取值一定时，字母式就有了确定的值，字母式的值随着字母的取值变化而变化，在感悟“变与不变”的过程中渗透函数思想。】

4.联系生活，介绍用字母表示数的历史。

师：游戏结束了，大树爷爷给小动物们颁发奖品。

师：这里的n可能表示什么？n×4呢？

生：n表示一盒巧克力的块数，n×4表示4盒巧克力的块数。

生：n表示一盒巧克力的质量，n×4表示4盒巧克力的质量。

生：n表示一盒巧克力的单价，n×4表示4盒巧克力的总价。

（隐去巧克力，只留下n×4）

师：在生活中，n×4还能表示什么？

生：n表示一列火车每小时的速度，n×4表示4小时行的总路程。

生：n表示一个足球场的面积，n×4表示4个足球场的面积。

生：n表示正方形的边长，n×4表示正方形的周长。

师：同学们生活经验很丰富。这么多不同情境下的4倍关系，现在只要用n×4这个式子都能概括出来！在数学发展史上，从用数字表示具体的数量到研究出用字母表示数和数量关系，经历了上千年的时间。

（播放“用字母表示数”的史料介绍）

【设计意图：数学教育只有在传授知识、培养能力的同时注重人文精神的渗透，才是健全的、完整的教育。渗透有关用字母表示数的数学史，使学生初步了解用字母表示数的思想方法产生、发展的过程，从中感受数学家严谨、锲而不舍的探索精神和创新精神，感受数学家对求真、求实的科学精神。】

三、灵活应用，巩固强化

1.框数中的规律。

（课件演示几个小动物框数）

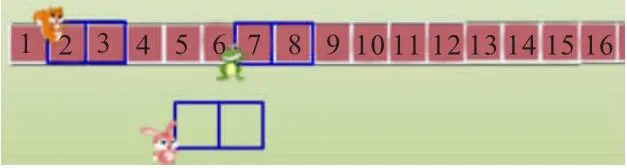
师：小兔子也用这个框子来框数，它可能框中几和几？

生：4和5。

生：11和12。

生：a和b，因为不确定它到底框中几和几。

师：再仔细观察每次框出的两个数，比一比，你有什么发现？

生：虽然框出的两个数在变化，但是它们都相差1。

生：后一个数比前一个数大1，前一个数比后一个数小1。

生：如果前一个数是a，那么后一个数就是a+1。如果后一个数是a，那么前一个数就是a-1。

师：抓住不变的关系来思考，你们具备了学好数学的优秀品质。

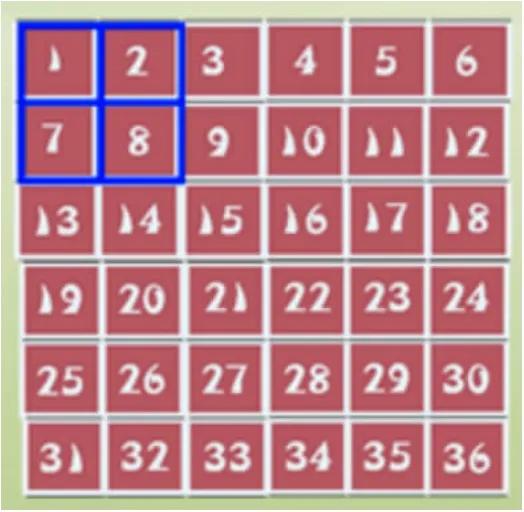
师：用这个田字框来框数，你能找到这四个数之间的关系吗？如果其中一个数用n表示，其他三个数又该怎样表示呢？（学生自己尝试，再在组内交流）

师：无论哪个数用n表示，虽然形式在变，关系是不变的。

【设计意图：在前面几个环节的体验中，学生感知到两个不同的对象，如果它们有关系，可以用字母式表示这种关系，这里设计两个框数游戏，引领学生的思维再次主动地飞跃，创造出字母式来表示变化规律，给以后的学习提供一个新的支撑，学生在遇到更为复杂的问题时，慢慢学会使用符号可以进行一般性的表达、运算和推理，进一步体会到用字母表示数的概括性和简洁性，发展学生的符号意识。】

2.字母表示计算公式。

师：如果周长用C表示，面积用S表示，你能用字母表示周长和面积的计算公式吗？（板书字母公式）

师：与文字叙述相比，你有什么感觉？

生：字母表示更简洁。

师：像这样含有字母的乘法式子还能写得更简洁。

（视频介绍简写规则，学生尝试简写）

师：再与原来的字母式相比，什么感觉？

生：数学追求的是简洁之美。

四、回顾总结，沟通联系

师：回顾这节课的学习，你有什么新的认识？

生：我知道了在不确定的情况下可以用字母来表示未知数。

生：我知道可以根据数量关系把数和字母一起运算写出字母式，字母式可以表示要求的数量，也表示数量关系。

生：用字母式还能更概括、更简洁地表示变化规律。

……

师：其实，用字母表示数我们并不陌生。以前我们用图形符号表示未知数，后来我们用字母表示运算律，今天我用字母表示未知数和数量关系，随着研究的深入，以后我们还会用它解决更多复杂的问题。

（演示一至五年级的相关知识生长过程）

【设计意图：符号意识是学生在长期的数学学习过程中通过体验和感悟养成的。课的最后不只进行简单的全课总结，更重要的是引导学生结合新知，重新审视以前的学习，联系小学阶段所经历过的用符号表示数的相关知识，建立具有良好结构的数学知识链，促进学生对用字母表示数的本质的理解，也为后续方程的学习积累有效的思维方法。】