通过例题培育逻辑推理能力的四个视角——基于数学多元表征学习

文|姚建法

推理与概念、判断都是思维的重要形式。逻辑推理主要包括演绎推理（从一般到特殊）、归纳推理（从特殊到一般）和类比推理（从特殊到特殊或从一般到一般）。苏教版教材例题承载着丰富的逻辑推理元素，通过例题培育逻辑推理能力需要多元而适合的学习方式得以护持，而数学多元表征学习正是其中一种重要的学习方式与行为路径。

数学多元表征是指同一个数学学习对象（如教材例题）可以用本质不同的多种表征形式进行数学化呈现，其本质是数学学习对象的替代。不同的例题背景、不同的年龄阶段，有着不尽相同的多元表征教学的应对，从而有助于小学生系统观察、有向猜想、结构论证、规范结论，进而培育小学生数学逻辑推理能力，发展数学思维。

一、基于多元表征学习的系统观察，是培育小学生数学逻辑推理能力的前提

自古以来，观察是人类认知自然、分析世界最直接、也是最为常用的方式。在小学数学课堂教学中，如何对观察对象（即逻辑推理对象）进行有理、有序、有向、有联的系统化整体观察？

【案例1】苏教版二年级下册《有余数的除法》。

图1

学生通过动作表征操作小棒或借助图像表征画图求解，完成了算式、填写了表格。

师：观察算式和表格，你有什么发现？

生：有4个算式商是一样的，中间3个算式有余数。

生：除数都是4，被除数每次加1，前4个算式商不变，最后一个商大了1。

生：余数都是相差1。

……

显然，教师的一句宽泛的“你有什么发现”使得学生的观察方向不聚焦，观察结果形成偏差，无意中增加了学生的认知负荷，未能达成认知目标。事实上，这是由于许多教师误认为青菜大卡通的问题“比较除法算式中的余数和除数，你有什么发现”过于聚焦不“开放”，限制了学生的思维。孰不知，此问紧扣余数和除法的大小关系，图表表征的因果逻辑清晰，十分有利于清晰地有向观察，展开逻辑推理：除数都是4，余数都比4小，降低了认知负荷。这样的定向系统观察，既节省了观察时间，减少了无意消耗，又提升了观察效能，为逻辑推理的有序进行与能力培育提供了前提可能。

二、基于多元表征学习的有向猜想，是培育小学生数学逻辑推理能力的关键

猜想，是人类发现并形成特定结论的常见起源。根据一组存在某种逻辑规律的事实，提出某种数学化的猜想，从而展开逻辑推理，获得新的命题，是培育数学逻辑推理能力的有效历程。而形成数学化的、有方向的猜想，才有助于进一步展开有效的验证，提高效能。所以，有向猜想是通过例题培育小学生数学逻辑推理能力的关键所在，是指向推理结论的“前奏”，其结论可能被证实、亦可能被证伪。

【案例2】苏教版五年级上册《钉子板上的多边形》。

图2

师：你们觉得它的面积可能和什么有关？

生：可能会和钉子的个数有关。

师：和哪里的钉子个数有关呢？先独自想一想，再和同桌轻声地说一说。

生：图形边上的钉子数和图形里面的钉子数。

师：钉子板上多边形的面积与它边上钉子数和里面钉子数又有怎样的关系呢？你们打算怎么来研究？

……

题组式平面图形面积的图像表征，学生隐约地直观感受到“数方格”“算面积”之外的“另一种方法可能”。此时“你们觉得它的面积可能和什么有关”的猜想，暗示了推理的方向。“和哪里的钉子个数有关呢”的追问则引领学生形成“有向”猜想：与多边形边上钉子数和里面钉子数有关。“又有怎样的关系呢？你们打算怎么来研究”更是敲打在数学内容的核心本质上，让学生的思维从“看得见的钉子”过渡到“寻找看不见的关系”以及“打算怎么来研究”的知识结构与方法结构上来，让逻辑猜想带有很强的数学方向与行动路径。于是，“透过数学本身的知识结构和教与学的结构化，数学的理性精神会根植于学生的头脑和血脉中。它虽然无形，却具有强大的力量，推动着学生以科学的方法不断探究新的世界、寻求新的发现、进行新的创造。”

三、基于多元表征学习的结构论证，是培育小学生数学逻辑推理能力的核心

在小学数学教材例题中，系统观察有一定规律的数学现象所提出的有向猜想，还需开展进一步的验证活动，而通过多元表征的证明或归纳的路径具有丰富性、逻辑性和多元性，存在形式化、格式化和结构化。学会结构论证，正是数学逻辑推理能力培育的核心所在。论证的路径丰富多元，如不完全归纳法的验证方式一般为举例验证，涉及特例与反例，具备论证的结构化模式；有一些猜想可以通过演绎证明、数形结合等方式展开，形成相互印证的结构系统。

【案例3】苏教版四年级下册《乘法分配律》。

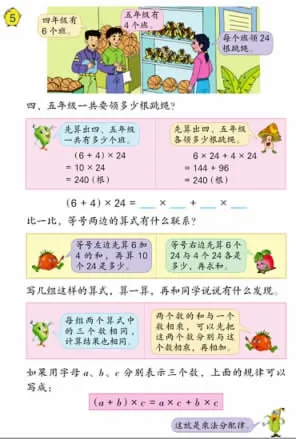
图3

路径一：符号表征。用不完全归纳的形式验证乘法分配律的猜想。“写几组这样的算式，算一算，再和同桌说说有什么发现”，既关注了算式等号两边的结构特征，更要真算、真比，判断是否真正两边相等，同时还需突出特例和尝试寻找反例。

路径二：情境表征。用数量关系论证乘法分配律的合理性（青椒与蘑菇小卡通的话语），引导学生讲好相似的“数学故事”。

路径三：言语表征。用乘法的意义论证乘法分配律的正确性，6个24加4个24，等于（6+4）个24，获得意义建构。

路径四：图像表征。应用两个等宽长方形的面积组合图直观感知与体验乘法分配律的必然性，实现数形结合。

事实上，学生已积累了加法交换律和结合律、乘法交换律和结合律的学习经验，对于不完全归纳法的推理论证应然熟悉：根据几个有规律的数学算式，提出猜想，而后举例验证并尝试寻找反例，最后得出结论并用字母符号表征运算律。而本课时，既关注了等号两边算式的结构形式，并以此经历结构化举例验证的不完全归纳推理过程，又开阔了学生的论证视角，拓展了教材的逻辑推理内涵与外延，分别展开情境表征突出数量关系、借助乘法意义进行言语表征、通过数形结合实施图像表征与符号表征，丰富了学生对于猜想验证的路径设想。

四、基于多元表征学习的规范结论，是培育小学生数学逻辑推理能力的保障

苏教版数学教材的例题，许多都具备丰富的背景性知识和过程性结构，体现出清晰而明确的逻辑推理样态。推理结论的表征样态可以是言语或文字的，也可以是图像的或符号的。然而，基于学生认知能力与年龄特点，通过逻辑推理形成的推理结论在数学表达上却又常常不够严谨与规范，导致一定程度上的思维脱节与思维弱化，需要教师适时引领，从而保证数学逻辑推理结论的有效确立。

【案例4】苏教版五年级下册《认识扇形》。

师：同一个圆中，扇形的大小与什么有关？

生：半径越大，扇形越大。

生：弧越大，扇形越大。

生：圆心角越大，扇形越大。

……

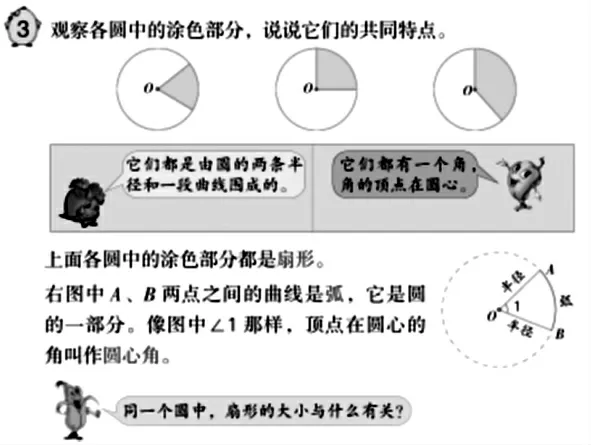
图4

此案例中，教师“无意识”地“应用”了教材中玉米大卡通的语言，对“同一个圆”这一大前提形成自我遮蔽，从而面对学生的回答中的思维漏洞视而不见。一定程度上，例题中三个同样大的圆在学生脑海中形成图像表征，导致学生潜意识里“默认为”扇形所在的圆同样大，从而这个“不变”的要素被忽视。由此，教师一方面需加强对学生逻辑推理思维过程严谨性的充分警觉，另一方面可以有意识地提供具备反例特性的图像表征，呈现一个半径特别大或特别小的扇形，组建图像表征组，直观对比中形成“反差萌”，明确同一个圆中影响扇形大小的要素有半径、弧、圆心角，它们“同大同小”，从而严谨推理思维，并用言语表征“不变+自变量+因变量”的范式规范表达：在同一个圆（或同样大的圆）中，弧（或圆心角）越大，扇形越大。

回归课堂主阵地，优化数学多元表征学习方式，充分将动作表征、图像表征、言语表征、符号表征等多元表征系统作用于苏教版小学数学教材例题教学，能够较好地促进数学理解，护持数学逻辑推理的理性认知与思维水平，提升学科关键能力。