基于实测的锚下有效预应力时变效应模型研究

张川龙 谢发祥 张 峰 阮 静

(河海大学土木与交通学院1) 南京 210098) (山东大学岩土与结构工程研究中心2) 济南 250061)(江苏省交通工程建设局3) 南京 210004)

0 引 言

拉脱法作为一种锚下有效预应力检测技术，又称为反拉法、提离法，具有测试精度高，操作方法简单等优点，在工程中得到了广泛的应用[1].在实际测试时，拉脱法仍然存在一些问题有待解决[2].文献[3]规定在张拉后24 h内应开展锚下有效预应力测试，但现场一般无法做到张拉后立即进行检测.工程实践表明：随着时间的推移，锚下预应力会出现一定程度的衰减.王向阳等[4]对现场制作的3片试验梁进行了预应力损失测试，结果显示3个月的预应力损失达到了10%，为150 MPa.同时在张拉后的2 d内预应力会出现急剧的下降，后期衰减速率又逐渐减小.管义军等[5]测试了3根混凝土小梁预应力随时间的变化，结果发现153 d后的预应力损失在140 MPa左右.其次，在张拉和检测两个时间点，环境温度往往存在差异，温度的变化同样会引起预应力的变化.

大跨径预应力混凝土桥梁中，混凝土收缩徐变和力筋松弛引起的预应力损失占总损失的30%以上，是预应力长期损失的主要影响因素[6].目前针对收缩徐变及预应力长期损失的预测模型很多，但不同模型得出的预测结果差异较大[7].究其原因：不同的收缩徐变及预应力长期损失预测模型考虑的影响因素不尽相同.混凝土及钢筋的材料特性、构件所处的外界环境本身也是一个随机变量，表现出较大的不确定性时变性[8].最后，混凝土收缩徐变与力筋松弛之间相互耦合[9].大量力筋的松弛试验表明，松弛随时间的发展规律具有一致性，均可以用对数关系或幂函数关系来描述.以上问题使得混凝土收缩徐变及力筋松弛在预应力长期损失中的构成及变化规律的预测变得比较困难.

同时温度变化对锚下预应力的影响也较为复杂.当温度升高时，一方面由于混凝土梁的膨胀导致预应力增加，另一方面温度升高对于力筋松弛以及混凝土徐变等因素具有的放大效应又会引起预应力减小.对于温度损失的预测，也有部分学者进行了研究.文献[2]研究了预制小箱梁500 h后预应力变化与温度变化的关系，结果表明二者存在明显的正相关性，并提出了考虑温度效应的拉脱法修正模型.葛琦等[10]进行了三峡永久船闸高边坡锚固工程监测，结果显示预应力变化与温度存在明显的滞后负相关性，预应力主要受当期和前两期温度的影响.

本文基于现场预制梁35束钢绞线开展了锚下有效预应力测试，通过数理统计分析获得了有效预应力损失的时间及温度损失预测模型，并与文献测试结果进行对比.通过分析，获得了不同预应力损失的变化规律、所占比例关系和48 h内锚下预应力相对稳定时间.

1 试验概况

1.1 测试样本

选取京藏高速JZ14标段30 m预制箱梁5片、JZ15标段30 m预制箱梁3片、20 m空心板1片、13 m空心板1片，累计10片梁.预制梁均采用C50高强混凝土；钢绞线采用直径15.2 mm，抗拉强度fpk=1 860 MPa，张拉控制应力σcon=0.75fpk.共张拉测试35根钢绞线，测试样本编号见表1.

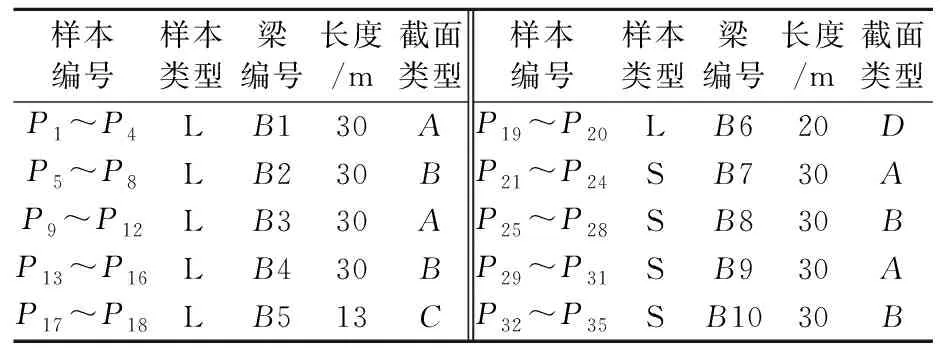
表1 测试样本及编号

1.2 测试方案

采用自动化综合测试系统进行锚下有效预应

力的实时采集，由上位机、采集模块(MCU)、系统软件、穿心式压力传感器及相关配件组成.

测试过程主要分为以下几个步骤：首先浇筑混凝土梁；然后在混凝土强度达到设计强度的90%以上后，穿束并在锚具与梁之间安装压力传感器，进行钢绞线张拉.最后连接自动化采集系统，采集锚下有效预应力随时间的变化.为准确测试预应力的变化规律，在72 h内每10 min采集一次数据，72 h后每1 h采集一次数据，连续采集一个月.

2 试验结果

2.1 主要测试结果

现场测试时每根钢绞线预应力采集时间从采集时间从张拉完成时刻开始，现场测试曲线见图1(仅示出部分实测数据).其中P1～P20的测试时间为30 d，P21～P35的测试时间为2～3 d.

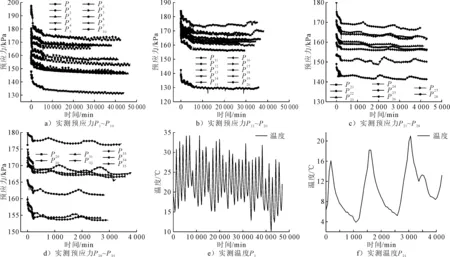
图1 现场测试数据

由图1可知：

1) 在锚固后800 h内，锚下有效预应力存在着整体衰减的趋势，其中在短时间内(大约10 h)衰减速率较大，之后衰减速率逐渐减小并趋于平稳.

2) 在整体衰减的同时，锚下有效预应力还存在明显的周期性波动，周期约为24 h.文献[2]表明，该周期性波动是由环境温度的周期性变化所引起.1个周期内温度与预应力的变化情况见图2.

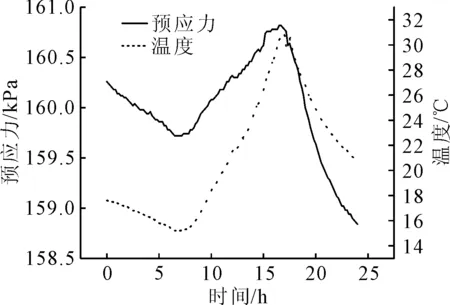
图2 一个周期内温度与预应力的变化情况

2.2 环境温度随时间的变化

根据文献[11]，环境温度T(t)可以描述为一条简单的简谐波曲线，即可以用式(1)来描述环境温度的变化.

(1)

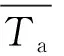
(2)

式中:ai(i=0,1,2,…,n)为多项式系数.经分析，当n=3时，拟合效果最佳.因此采用三次多项式来描述环境平均温度的变化.利用式(2)对35个样本曲线进行温度数据拟合，部分样本拟合结果见图3.样本环境温度数据拟合的R2见表2.

由图3和表2可知，环境温度的拟合程度较高.为了确定式(2)中各参数的取值，选用显著性水平α=0.05，采用柯尔莫哥洛夫-斯米尔洛夫检验法[12]对温度拟合式(2)参数进行正态分布假设检验.原假设H0：A1,ta,τ,a1,a2,a3服从正态分布.分布拟合假设检验结果见图4.(仅列出参数A1检验结果).检验结果显示各参数均服从正态分布，统计20个长期测试样本温度拟合参数见表3.

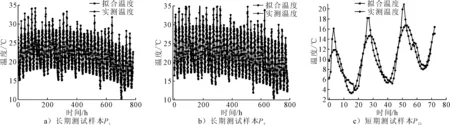
图3 样本温度数据拟合结果

表2 温度拟合R2统计

表3 温度拟合参数均值及95%上下限统计

根据式(2)可以得出任意时间的环境温度变化量为

ΔT(t)=T(t)-T(0)=

(3)

3 预应力长期损失预测模型

预应力长期损失的预测主要有总体估算法、分项计算法及时步分析法3类.分项计算法被各国规范所采用，将各项预应力损失进行分别计算再叠加.由以上讨论可知，在张拉锚固后任意时刻锚下有效预应力损失由预应力钢筋松弛损失、混凝土收缩徐变损失及温度变化损失组成，即锚下有效预应力长期损失预测模型可以表示为

y=yR+yc+ys+yT(t)

(4)

式中：y为锚下有效预应力总损失率；yR为松弛率；yc为徐变损失率；ys为收缩损失率；yT(t)为温度变化损失率.

3.1 预应力钢筋松弛损失预测模型

采用ACI209规范推荐的模型来计算低松弛钢绞线的松弛损失.考虑收缩徐变的影响，在式(5)中引入λ作为松弛折减系数，取值为0.8.

(5)

式中：σp0为初始应力；fpy为预应力筋屈服强度；t为持荷时间.

3.2 混凝土收缩徐变损失预测模型

任意时刻收缩徐变损失规律的时变预测模型主要有CEB-FIP90模型、PCI-BDM模型及我国桥规JTG2018模型等.从收缩徐变损失预测模型表达式的共同形式可以看出，混凝土收缩徐变损失时变模型可描述为式(6)～(7).

yc=A·φ(t,t0)

(6)

(7)

式中：A为待定参数；Ec为28 d龄期混凝土弹性模量；σpc为预应力钢筋重心处由预应力产生的混凝土法向压应力；φ(t,t0)为徐变系数；εcs(t,t0)为收缩应变；t0为加载龄期；t为计算龄期.

由此可见对于收缩徐变损失的预测，首先需要准确预测混凝土收缩徐变引起的变形.已有研究表明，国内外规范的不同的计算模型对于收缩徐变的计算结果差异较大.袁鹏飞[13]的研究结果表明修正ACI模型的预测效果均高于已有规范模型.采用文献[13]提出的修正ACI模型计算收缩徐变.其中，徐变系数为

(8)

φc,∞=2.35(1.5-0.012fcm)γt0γhγRHγSγψγα

(9)

式中：fcm为28 d龄期混凝土立方体抗压强度平均值，φc,∞为徐变系数终极值；Hcr=12-0.08fcm；γt0为加载龄期影响系数；γh为理论厚度影响系数；γRH为相对湿度影响系数；γS为坍落度影响系数；γψ为细集料影响系数；γα为空气含量影响系数.

收缩应变计算模型为

(10)

εcs,∞=780×10-6(1.2-0.008fcm)·

γRHγVSγSγψγCγα

(11)

式中：εcs,∞为收缩应变终极值；ts为干燥龄期；γVS为构件体表比影响系数；γC为水泥含量影响系数；Hsh=40-0.3fcm.

综合上述式(6)～(11)，本文拟采用的徐变收缩损失预测模型见式(12)～(13).

(12)

(13)

式中：B1，B2为待定参数.由于修正ACI模型时间发展系数未考虑环境相对湿度、构件理论厚度等因素，因此在公式中增加参数B1，B2用于反映二者的影响.参考混凝土结构设计规范及CEB-FIP90规范给出的混凝土收缩徐变损失计算公式，参数A、B1、B2为

(14)

B1=k1·0.35·h2

(15)

B2=k2·{0.15[1+(0.012RH)18]h+250}

(16)

式中：k,k1,k2为待定系数；k为预应力钢筋松弛对于收缩徐变损失的折减效应；ρps为纵向钢筋配筋率；h为理论厚度；RH为环境相对湿度.

3.3 温度变化损失预测模型

预应力变化与预应力钢筋温度变化之间存在线性相关性，为

Δσ=κ·EpαpΔTs(t)

(17)

式中：Δσ为预应力变化量；κ为与钢筋与混凝土之间的有效黏结有关的系数；EP为预应力钢筋弹性模量；αP为预应力钢筋线膨胀系数；ΔTs(t)为预应力钢筋温度变化.

考虑到预应力筋温度变化与环境温度变化存在时间上的不同步，引入一个滞后期d来描述，为

ΔTs(t)=ΔT(t-d)

(18)

式中：ΔT(t-d)为(t-d)时刻的环境温度变化.将2.2式(3)中时间变量t代之以(t-d)，即得：

ΔT(t-d)=

(19)

因此，将环境温度变化引起的预应力损失预测模型为

(20)

3.4 拟合结果

采用式(4)及各分量模型对35个样本锚下预应力实测损失进行拟合分析，部分样本拟合结果见图5，各样本拟合曲线R2见表4.

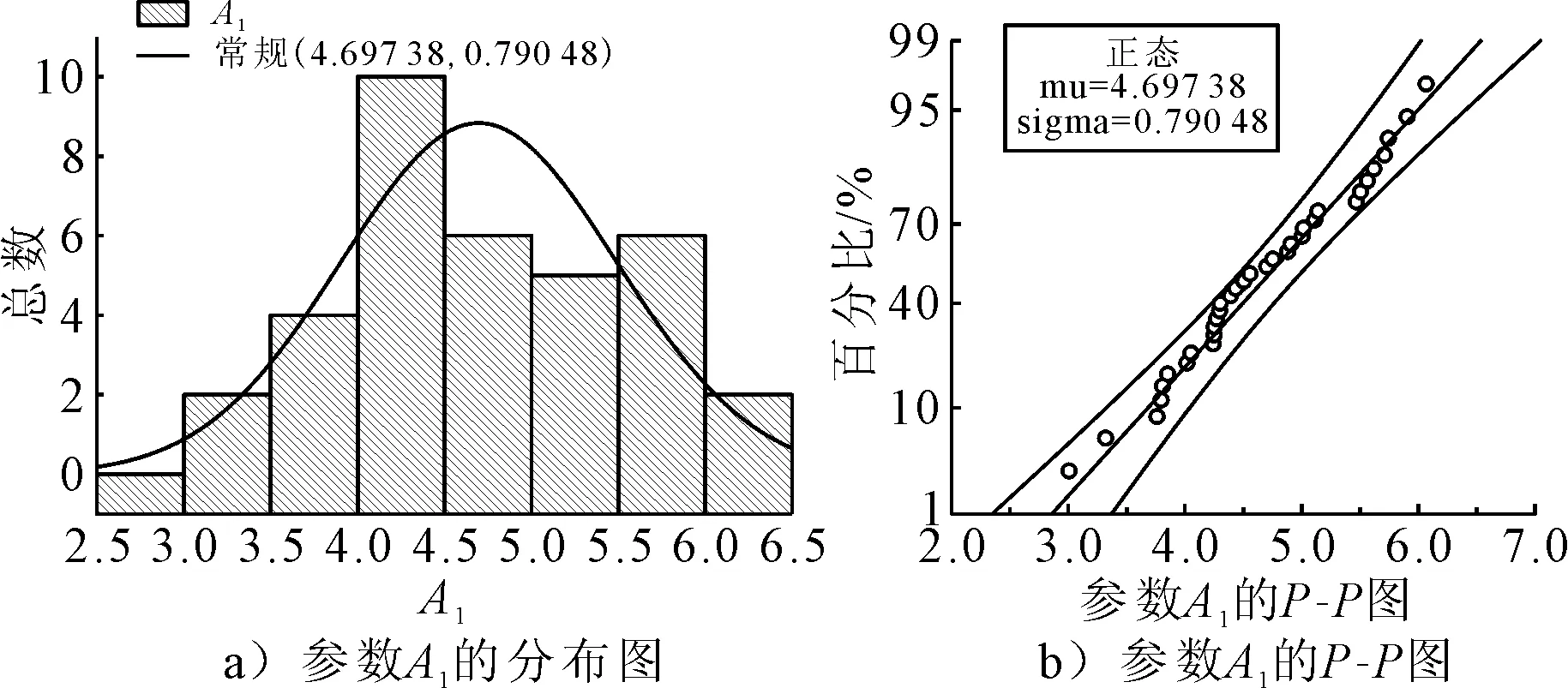
图5 参数A1假设检验结果

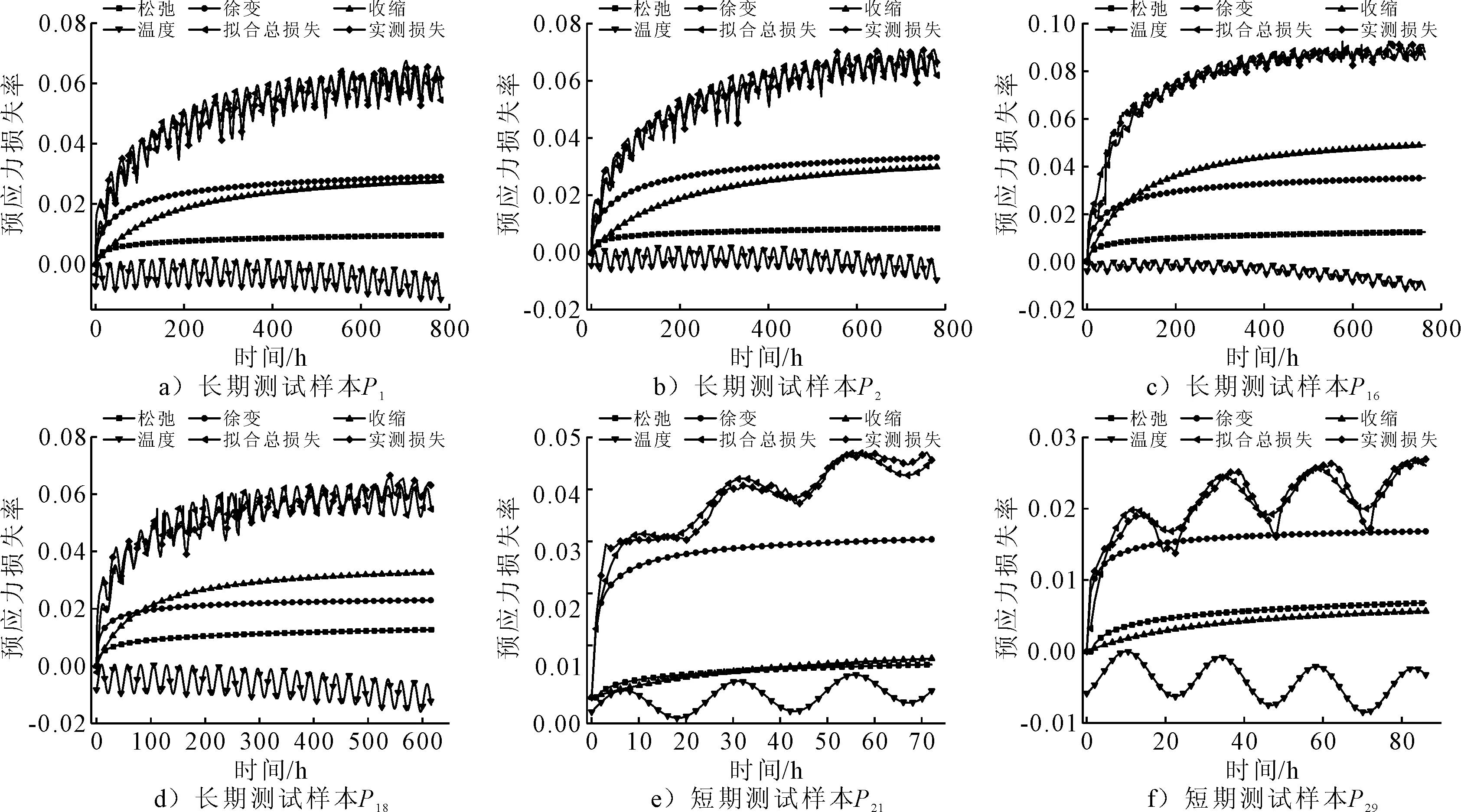
图5 预应力损失拟合结果

编号R2编号R2编号R2编号R2编号R2编号R2编号R2P10.93P60.94P110.93P160.96P210.94P260.70P310.93P20.96P70.94P120.97P170.85P220.95P270.91P320.97P30.93P80.96P130.88P180.84P230.94P280.92P330.91P40.94P90.91P140.91P190.98P240.96P290.86P340.91P50.89P100.82P150.88P200.93P250.93P300.88P350.95

由表4可知：34个样本预应力损失拟合R2均在0.8以上，仅P26为0.7，这表明式(4)拟合效果较好.统计长期测试样本P1～P20每100 h及短期测试样本P1～P35每1 h各项预应力损失率的大小见图6.

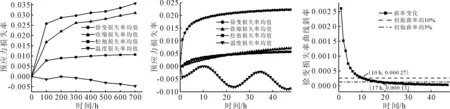
图6 预应力损失统计

由图5～6可知：

1) 800 h内，混凝土收缩徐变损失占据预应力损失主要部分，相对于收缩徐变来说，松弛损失影响较小.各项预应力损失影响程度比较：徐变损失>收缩损失>松弛损失>温度变化损失.

2) 48 h内，预应力损失速率较大主要是由于混凝土徐变发展较为快速.由48 h内徐变损失曲率变化可知，10 h后徐变发展的曲率已减小至初始曲率的10%，17 h后减小至5%.因此，建议实际工程中拉脱法的测试时间点选在张拉后(17～24) h.

3.5 模型参数分析

根据35个测试样本的拟合A、B1、B2值计算出k,k1,k2值.选用显著性水平α=0.05，采用柯尔莫哥洛夫-斯米尔洛夫检验法对得出的系数k,lgk1,lgk2,κ,d进行正态分布假设检验.原假设H0：k,lgk1,lgk2,κ,d均服从正态分布.分布拟合假设检验结果见图7(列出k,κ,d的结果).检验结果显示各参数均服从正态分布.分别计算k,lgk1,lgk2,κ,d的均值及其95%上下限，结果见表5.

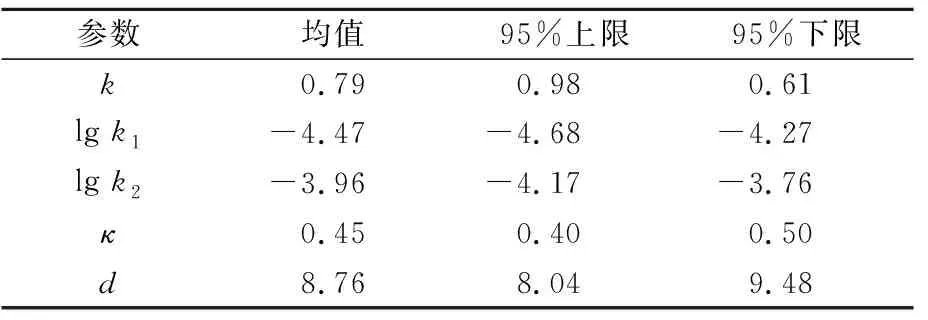
表5 收缩徐变拟合参数均值及95%上下限

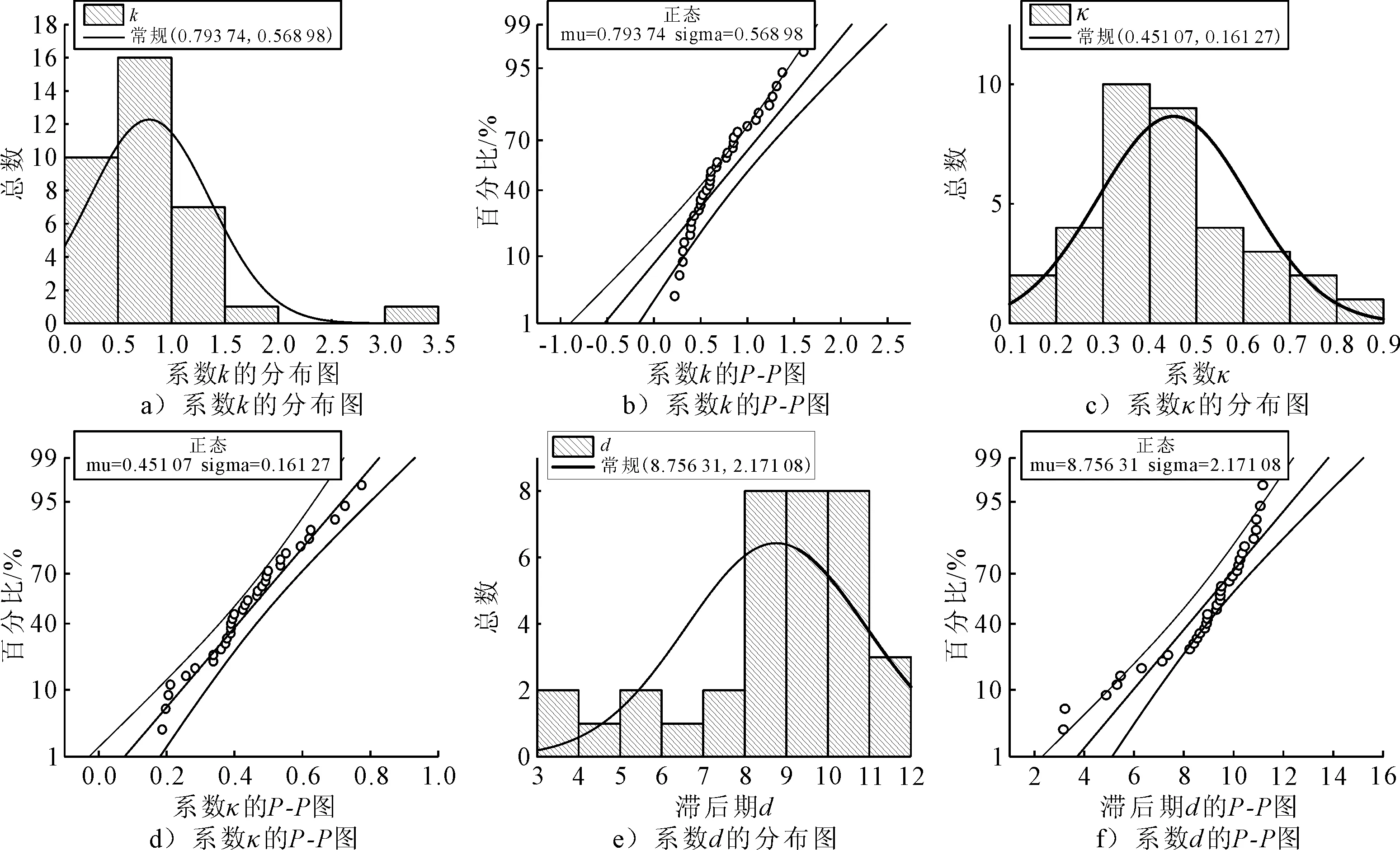
图7 收缩徐变参数假设检验结果

3.6 模型验证

为了验证模型(4)的预测效果，选取文献[2]中陕西太凤高速、西宝高速、柞山高速的5根钢绞线锚下有效预应力实测数据与预测值进行对比.由于没有温度实测数据并且从3.4的分析可知温度的影响较小，因此不计算温度变化损失.5根钢绞线预应力损失实测数据与预测模型计算结果对比见图8.

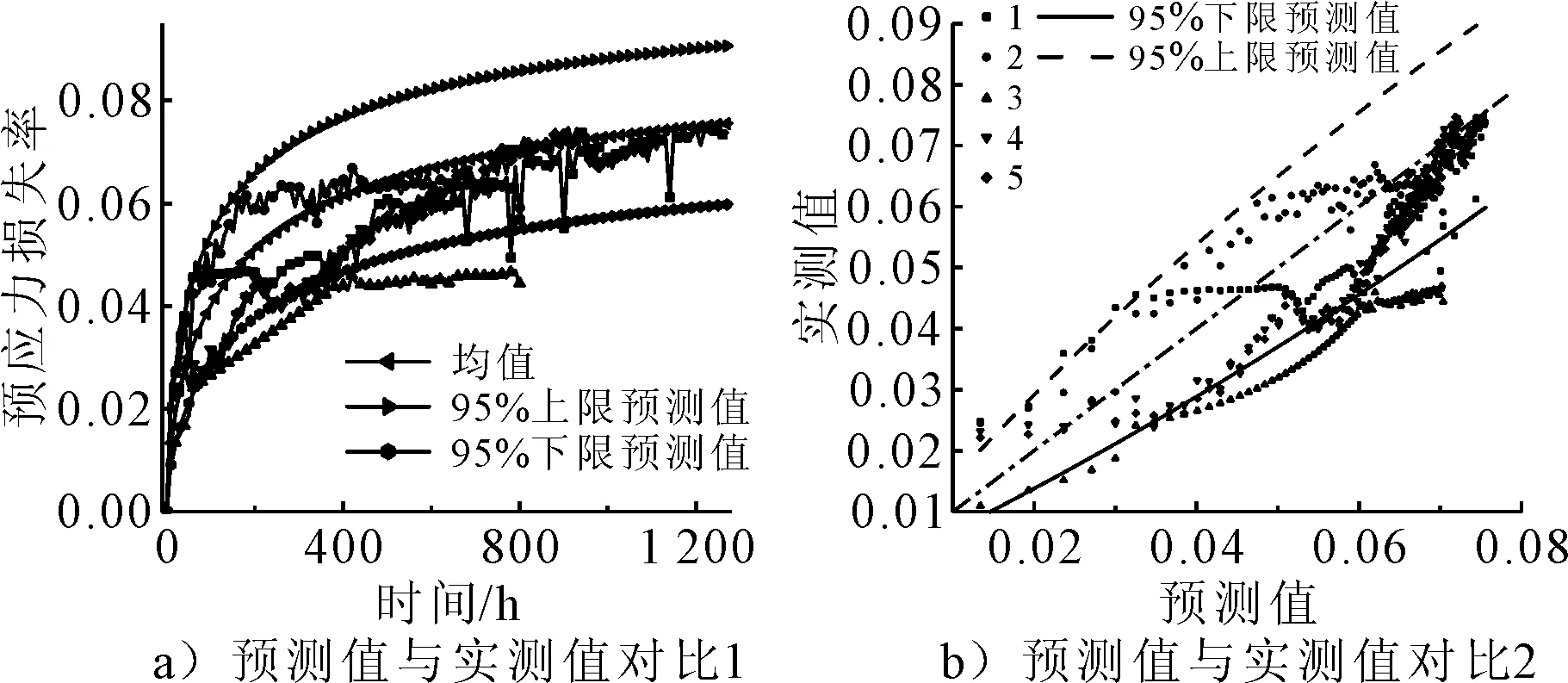
图8 模型预测效果验证

由图8可知：5根钢绞线的预应力损失实测值均在95%上限预测值以下，而有1根钢绞线的预应力实测损失低于95%下限预测值.对比结果说明模型(4)的预测效果较好，可以用于实际工程的预应力损失计算.考虑到工程实际情况，应用时选用95%上限预测模型进行计算.

4 结 论

1) 800 h内，锚下有效预应力的整体衰减主要由松弛损失、收缩损失、徐变损失及温度变化损失引起.其中，收缩徐变损失占总损失的主要部分，松弛及温度变化损失影响小于混凝土收缩徐变.

2) 72 h内，锚下有效预应力的快速衰减是由于混凝土徐变的快速发展，17 h后的徐变损失曲率为初始曲率的5%，建议将拉脱法的测试时间选在张拉后(17～24) h.

3) 通过样本数据拟合得出了预应力长期损失预测模型并与实测值进行对比，结果显示5根钢绞线的预应力损失实测值均在95%上限预测值以下，而有1根钢绞线的预应力实测损失低于95%下限预测值.对比结果说明模型的预测效果较好，可以用于实际工程的预应力损失计算.