取消省界收费站对货车驾驶员行为选择影响的Logit模型研究

梁亚莉 郭永健 郑欢欢 李杲岭 崔洪涛

(郑州综合交通运输研究院有限公司1) 郑州 450018)(河南省高速公路联网监控收费通信服务有限公司2) 郑州 450018)

0 引 言

取消全国高速公路省界收费站，减少车辆在高速公路省界收费站的等待时间，提高通行效率.收费模式也由原先的最短路收费改为按照车辆实际行驶路径收取通行费，货车由原先的计重收费改为按车型收费，即同一辆货车空车、重车收费相同.

因此，货车驾驶员是对省界收费站取消后实行的新政策产生敏感性最高的群体，可能会改变高速公路还是国、省干道作为新的路径选择策略.

离散模型作为分析个体行为选择的最有效方法，为此国内外学者做了大量的研究.Emmerink等[1]从驾驶员的个人属性的性别、年龄，以及道路等级方面分析了驾驶员出行时的路径行为选择.Bekhor等[2]考虑了驾驶员的家庭因素、婚姻状况等，研究对驾驶员出行时选择路径产生的影响.Limtanakool[3]等分析了出行距离对出行方式的影响，建立了BL(Binary Logit)，从社会经济、时间、土地开发强度等维度分析了出行方式选择，结果表明该模型对出行行为方式的解释性较高.高鹏[4]从驾驶员偏好数据方面，分析相关因素，建立了路径行为选择的模型.边超等[5]利用灵敏度分析方法，分析了公路费率与货车流量之间关系.

文中通过分析货车驾驶员在取消省界收费站后路径选择的影响因素，引入灵敏度分析理论对影响因素进行敏感性分析，构建了基于取消省界收费站的MNL驾驶员行为选择模型.

1 数据来源

1.1 出行行为分析

取消高速公路省界收费站后，货车驾驶员在运输过程中的路径选择行为也受到较大影响，出行决策分别为：

1) 改变出行方式 随着高速公路实施新的收费政策，ETC货车用户在前期具有费用减免政策，根据测算货车平均通过省界时间由原来的29 s减少为3 s，下降了89.7%.在通行效率方面高速公路对货车的吸引远高于小型汽车，因此在短期内改变高速公路的路网结构.

2) 改变出行路径 取消高速公路省界收费站前，主要采用封闭式收费制式，客车按车型、货车按重量，根据路径和里程进行收费，分路段拆账，大多数省份高速公路收费采用最短路径收费.取消省界收费站后采取据实收费策略，原高速公路单一路径转变为高速公路-国省干线等的组合路径或国省干线单一路径进行分担，来应对高速公路新的收费政策.

3) 改变出行时间 受节假日等优惠策略影响，货车驾驶员会调整高速公路使用的优先级.

4) 无影响 货车驾驶员的路径选择行为不受省界收费站的影响，一般多发生在公司级货物运输车辆中.

1.2 出行因素分析

取消省界收费站后，货车驾驶员路径选择行为因个人属性、货车属性、货物运距、货物时效性、高速公路收费政策等的不同而不同.文中从货车驾驶员的个人属性、车辆属性、政策属性等方面制定基于能够反映个体偏好的SP调查[6]，见图1.

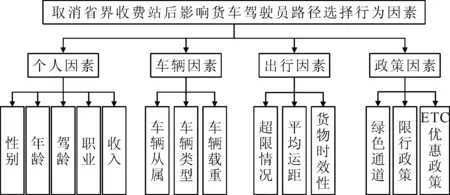
图1 货车驾驶员路径行为选择影响因素

根据2019年高速公路车辆车型中货车(专项作业车)车型分类标准、总轴数，以及车长和最大允许总质量由原来的五类车型调整为六类车型.同时将两轴车辆进一步细分为两类，车长和最大允许总质量作为第二指标，对两轴车辆进行细分.本文参考2019货车最新分类标准作为本次SP调查的货车类型依据.

1.3 数据调查

于2020年5月在河南省郑州、洛阳、南阳等市根据城市规模确定本次调查点个数，样本分布见表1.

表1 货车驾驶员调查样本分布

发放为期3 d的调查问卷，针对货车驾驶员可能会产生的疑问进行解释.本次调查共发放问卷520份，回收有效问卷512份，剔除不完整问卷后获得有效问卷478份.本次调查结果显示：男性432人，女性46人，年龄范围在22～56岁，平均年龄38岁，所驾驶货车车辆类型分布见表2.

表2 货车类型分布情况表

2 货车驾驶员非集计Logit模型

2.1 模型理论

取消省界收费站后，假设货车驾驶员n受到影响，此时路径选择集合为Cn，选择路径i的效用为Ui，则该货车驾驶员从集合Cn中选择路径i的条件为

Uin>Ujn,i≠j,j∈Cn

(1)

由于受到取消省界收费站的影响，货车驾驶员选择路径i视个人特性、车辆因素、出行因素、政策因素等可能发生改变，因此将效用Ui视为随机变量，其具体形式为

Uin=Vin+εin

(2)

式中：Vin为货车驾驶员n选择路径i的效用函数固定项；εin为相应的概率项.

根据效用最大化理论，计算出货车驾驶员n选择路径i的概率为

Pin=Prob(Uin>max(Ujn),i≠j,j∈Cn)

(3)

2.2 MNL构建

多项式Logit模型(multinominal logit model，MNL)[7]假设效用函数Uin中的概率项εin相互独立，服从Gumbel极值分布，则对于εjn(j=1,2,…,Jn)的联合分布函数为

(4)

效用函数Ui中的固定项Vin由货车驾驶员选择方案集合Cn，影响因素向量确定，其形式为

(5)

式中：θ=(θ1,θ2,…,θk)为未知参数向量；Xin=(Xin1,Xin2,…,Xink)为货车驾驶员n选择路径方案i的影响因素，其中Xin1为固有哑元.

由此可以计算得到选择概率模型，具体形式为

Pin=Prob(Uin>Ujn,i≠j,j∈Cn)=

Prob(Vin+εin>Vjn+εjn)=

(6)

结合效用函数Ui各子项具体形式确定货车驾驶员MNL模型选择概率为

(7)

通过对影响货车驾驶员路径选择影响因素分析，同时考虑MNL的0-1变量特性，综合确定MNL模型效用函数的变量，见表3.

表3 效用函数变量

在变量选择中，考虑到货车驾驶员实际路径选择过程中的实际情况，将θ3和θ6设为通用变量，θ1、θ4、θ7、θ9等其余项设为特定项，由此确定本文MNL模型的效用函数为

Uin=ASCin+P*θ1+R1*θ2+R2*θ3+

R3*θ4+O1*θ5+O2*θ6+O3*θ7+

S1*θ8+S2*θ9+S3*θ10+εin

(8)

式中：ASCin为选择方案哑元，待估计常项.

3 模型检验

3.1 MNL参数估计及检验

在构建MNL模型中，假设在取消高速公路省界收费站后，货车驾驶员路径选择集合为，Cn={高速公路、国省干道、高速公路-国省干道}，对应路径标号为Cn={1,2,3}.本模型路径选择对国省干道为相对效用.货车驾驶员在获取到取消省界收费站的信息前提下，考虑到有关费用及运输时间等因素后改变货车路径决策，国省干道转变为高速公路或高速公路-国省干道路段组合的行驶路径，或不改变原计划路径选择决策.

应用Biogeme软件，对本文构建的基于取消省界收费站后的货车驾驶员路径选择行为MNL模型进行参数标定，其结果见表3.标定参数后，确定模型中显著影响因素，采用t值进行检验，其形式为

(9)

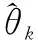
当tk>1.96则说明有95%的可靠性说明货车驾驶员路径选择的第k个因素对其路径选择产生显著影响.ρ2为模型的优度比，其值介于0～1，值越大则认为模型的精度就越高.

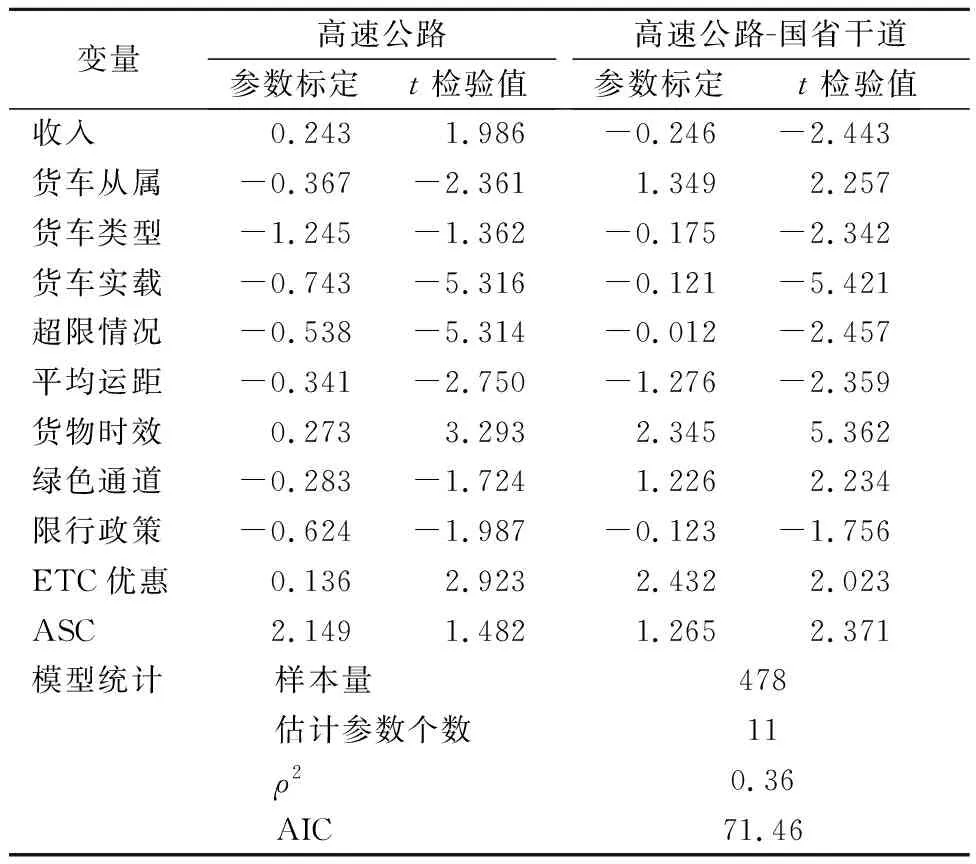
表4 MNL模型参数标定结果

从MNL模型的参数标定结果看，虽然货车类型、ETC优惠、绿色通道、限行政策等因素的t检验值小于1.96，但不能说明其毫无影响，仍需要保留[9].其余变量的检验值均大于1.96，说明该部分影响因素能够在取省界收费站时对货车驾驶员路径选择产生显著影响.收入水平、货物时效性越高、ETC优惠力度越大等选择方案的效用值越大.本次构建模型的优度比ρ2为0.36，说明该模型处于合理范围内.

3.2 影响因素的灵敏性分析

引入灵敏度分析有关理论，确定各影响因素对货车驾驶员路径选择的弹性值.在文中MNL基础之上，构建各路径选择的弹性模型，其形式为

R=100×θkXink(1-Pin)

(10)

式中：Xink取数据调查统计中对应属性变量的平均值.

对弹性值进行解释：当|R|=0时表示无弹性；|R|∈(0,1)时表示弹性较弱，缺乏弹性；|R|>1或等于1时表示富有弹性或单位弹性；|R|→∞表示具有完全弹性.

根据本次调查问卷计算各属性变量Xink的平均值，结果见表5.

表5 驾驶员各属性变量平均值

由表5可知，对不同路径选择方式其变量平均值差别较大，对选择高速公路作为运输路径来说，收入水平在8 000元以上，5～6类的货车类别、平均运距300 km等是选择该运输方式的主要因素.对选择国省干道单一路径作为运输方式的货车驾驶员来说，私人货车、货车满载、平均运距100 km以内等选择该运输方式的主要原因.高速公路-国省干道组合运输策略的因素介于两者之间.进一步计算出车辆因素对货车驾驶员路径行为选择的灵敏性大小，结果见表6.

表6 车辆因素灵敏性值

由表6可知，车辆从属关系、货车类型、货车实载对高速公路及国省干道均富有弹性，即该因素的变化对货车驾驶员是否继续选择高速公路活国省干道作为运输方式存在较强的动态变化影响.货车类型、货车实载对运输方式高速公路-国省干道的弹性较小，缺乏弹性.同时分别计算各效用变量属性的灵敏度值，计算结果见表7.

表7 不同路径选择的灵敏值

由表7可知，个人因素中的收入水平对路径方式高速公路、国省干道的敏感性较强，绝对值均大于1，属于富有弹性范围，而高速公路-国省干道的敏感性较小，属于缺乏弹性，且高速公路路径选择的灵敏性大于国省干道的灵敏性，说明货车驾驶员收入水平的高低对是否选择高速公路作为运输路径存在较大影响.车辆因素对路径选择的灵敏度不一，货车从属关系(公司货车或私人货车)对国省干道路径选择的灵敏性最高，说明当货车从属关系不同，相较于其他两种运输路径，对货车驾驶员选择国省干道影响程度更大.货车类型及货车实载对高速公路这一路径的敏感性较高，比较符合实际.在出行因素中，货物时效性这一影响因素对国省干道的灵敏性最高，其值为2.429.

3.3 统计验证分析

将本次货车驾驶员行为选择路径概率选择预测结果与河南省高速公路联网等相关数据进行验证分析，结果见表8.

表8 模型预测与实际统计结果 单位：%

由表8可知，单一路径的国省干道运输方式预测结果与实际观察的误差率较大，其值为18.6%.而高速公路、国省干道-高速公路这两种运输路径的模型误差率较小，分别为7.7%、9.1%，说明了笔者构建的货运驾驶员路径选择模型具有一定的准确度.

为进一步分析影响货车驾驶员运输路径选择行为的影响因素，选取省界收费站取消前后同期6—9月份(2019年与2020年)进行验证分析.选择货车交通量、平均载货量为本次验证的定量指标.调查点郑州、洛阳、许昌、南阳、周口5市同期货车交通量见图2.

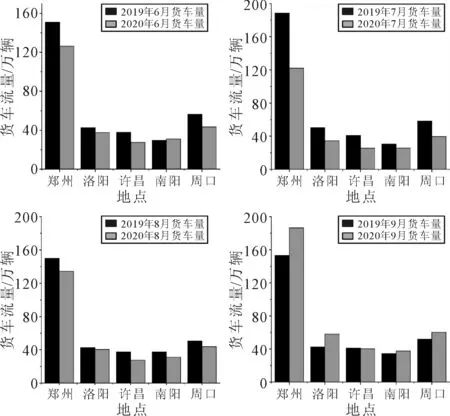
图2 高速公路货车交通量统计结果

由图2可知，除9月份外，2020年的6月、7月、8月的各统计点货车交通量较2019的同期均有所下降，说明随着省界收费站的取消对于货车驾驶员来说，高速公路这一路径选择是属于非最优选择，该统计结果与构建的MNL模型的路径选择概率相一致，符合预期目标.为验证模型的车辆因素对货车驾驶员路径选择的影响，依托河南省高速公路联网数据，测算省界收费站取消前后(2019年、2020年)货车的平均载重指标，分析高速公路这一运输路径中对货车驾驶员行为选择的影响程度.结果见图3.

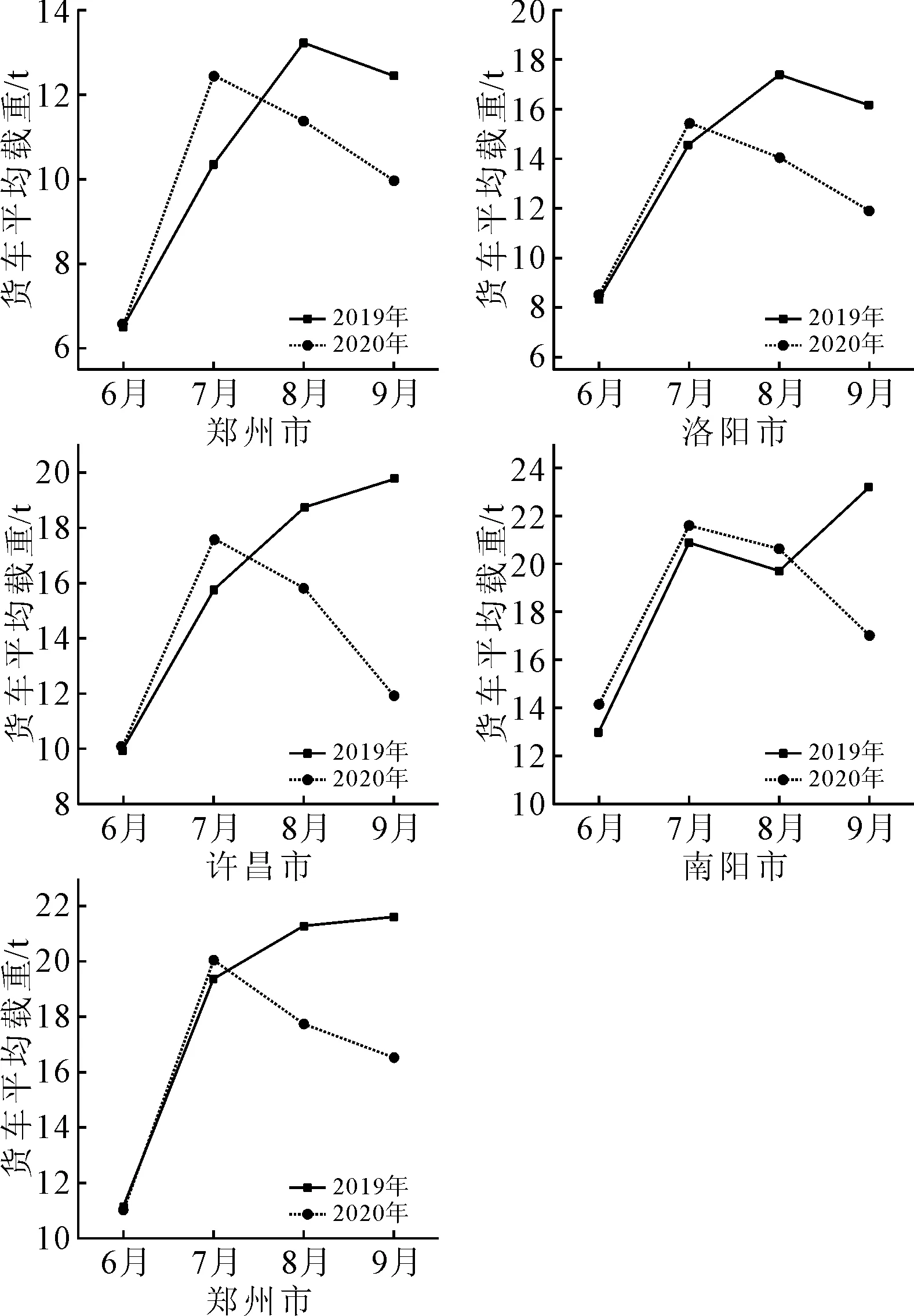
图3 高速公路货车平均载重

从各核查点的货车平均运输载重结果可以看出，2020年除6—7月份货车平均载重均出现增长外，选定的其他月份货车平均载重均出现下降趋势，同时除南阳市以外，8—9月份的货车平均载重均低于去年同期.结合图2高速公路货车流量的变化情况，分析其主要的原因在于省界收费站的取消改变了以往货车通行费计费方式，即由按重量计费规则变成按货车轴数收费的标准，轴数越多的货车更多的改变了货运路径选择方式，间接降低了高速公路的货车平均载重.根据在本模型的灵敏度计算结果，货车驾驶员路径选择的车辆类型的灵敏度计算值7.726，属于富有弹性，从模型的角度确定了取消省界收费站后，新的收费政策对货车载重情况存在一定影响.这一统计结果与文中构建的MNL模型结论一致，即货车实载对高速公路这一选择路径的灵敏性较大.

4 结 论

1) 以货车驾驶员路径选择方式作为研究对象，通过个人属性、货车属性、出行属性、政策属性等4个维度确定了影响货车驾驶员路径选择行为的因素，构建了以高速公路、国省干道、高速公路-国省干道等路径的选择肢.

2) 通过问卷调查方式获取数据源，标定本文构建的MNL模型参数，确定了影响值.为具体分析各因素影响效益值，引入灵敏性分析理论，确定了各因素对路径选择方案的灵敏度.

3) 模型结果表明，收入水平对各选择肢均产生较高的灵敏性，货车从属关系对高速公路-国省干道这一选择肢的灵敏性较强，货车类型及实际载重对高速公路这一选择肢产生较大的影响.

4) 文中构建的MNL模型的标定结果符合实际，能够应用对货车驾驶员路径选择的行为分析.