考虑空间异质性的城市建成环境对交通拥堵状态的影响

袁 浩 任 杰 杨 睿 朱 彤* 李博超

(长安大学汽车学院1) 西安 710064) (长安大学运输工程学院2) 西安 710064)

随着我国城市化的快速发展，交通拥堵问题愈发严峻，并已成为制约城市发展的瓶颈.交通拥堵不单纯是交通系统本身的问题,其本源是土地利用格局导致的交通供需失衡，所以精准把握城市建成环境中土地利用与交通基础设施对交通拥堵状态的影响，对缓解交通拥堵具有重要意义.

目前已有学者就土地利用与交通基础设施对交通拥堵状态的影响展开研究.Ewing等[1]研究发现居民通勤时间与土地混合利用指数呈负相关，人均延误与中心度呈负相关.何树林[2]认为发生交通拥堵的根本原因是交通供需失衡诱发的交通流运行状态失稳.Wang等[3]发现土地利用和交通设施不匹配是导致城市土地重建后交通拥堵的直接原因.王家庭等[4]对我国35个大中城市交通拥堵水平测度，发现城市空间结构、路网密度在一定程度上会导致交通拥堵.郑思齐等[5]证明了职住失衡与公共服务过度集中是导致城市内部交通拥堵的重要原因.王新军等[6]发现居住、办公与商业用地密度，路网密度等对交通拥堵有显著影响.张振龙等[7]发现拥堵时空分布规律与交通供需、路网结构、职住分离、用地布局等因素存在一定相关性.

已有研究虽从城市建成环境各角度对交通拥堵状态展开了分析，但都忽略了交通拥堵影响因素的空间异质性，即城市建成环境在不同地理位置对交通拥堵状态的影响程度差异性.地理加权回归(geographically weighted regression，GWR)模型作为一种能有效揭示被观测者空间异质性和空间相关性的方法，近年来广泛应用于居民出行时空、公共交通出行需求、共享单车分布特征等交通领域的空间异质性研究.

鉴于此，文中以西安中心城区为案例开展实证研究，运用地理加权回归模型定量分析城市建成环境变量对交通拥堵状态影响的空间异质性，并通过与传统的普通最小二乘法(ordinary least square，OLS)进行比较，验证地理加权回归模型对交通拥堵状态分析的适用性，以期为城市交通规划与管理提供理论依据.

1 研究数据与处理

1.1 研究区域概况

本研究区域为西安中心城区(见图1)，面积约为826 km2，以研究区域内的55个街道为基本研究单元.

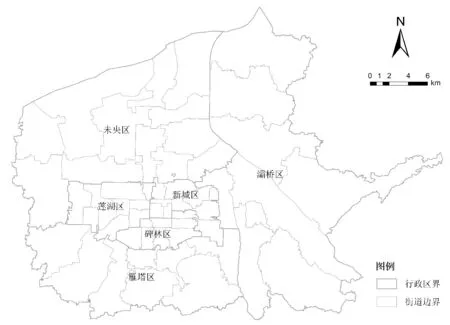
图1 研究范围

1.2 因变量的确定

以拥堵延时指数作为量化区域交通拥堵状况的指标.计算路段拥堵延时指数，基于Arc GIS平台的差值功能的反距离权重法(IDW)进行差值，利用分区统计工具得到各街道的拥堵延时指数.其中，路段拥堵延时指数计算公式为

(1)

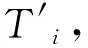
通过高德地图开放平台获取研究区域2020年6月各工作日02:00—04:00、早高峰07:00—09:00及晚高峰17:00—19:00的路段速度，通过上述方法计算各街道早晚高峰的拥堵延时指数，见图2，工作日晚高峰的拥堵延时指数要明显高于早高峰.鉴于此，本研究主要分析晚高峰时段街道层面的交通拥堵状况，区域交通拥堵严重程度为：碑林区>新城区>莲湖区>雁塔区>未央区>灞桥区.

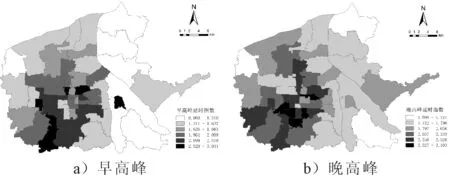
图2 早晚高峰拥堵延时指数

1.3 建成环境变量的确定

1.3.1建成环境变量选择

将建成环境定义为提供人类活动需求而建设配置的人为空间环境，包含土地利用形态、交通基础设施，以及城市道路设计等因素.在交通领域，建成环境由以下五个要素来描述：密度(density)、混合度(diversity)、设计(design)、公交邻近度(distance to transit)与目的可达性(destination accessibility).在此基础上对建成环境“5Ds”因素具体度量，采用人口密度、土地利用混合度、停车位密度等10个建成环境变量作为备选自变量，结果见表1.

表1 建成环境“5Ds”因素度量指标

1.3.2建成环境变量测度

基于Arc GIS平台的核密度工具计算企业密度、路网密度等密度指标.以企业密度为例，首先去除数据中异常和重复值，并对无效数据进行清理和修正；随后利用Arc GIS平台的核密度工具估计企业密度在整个研究空间上的分布；最后利用分区统计工具获取各街道的平均企业密度.其他密度指标处理方法如上.核密度计算公式为

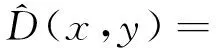
(2)

土地利用混合度通过熵指数进行衡量，取值介于0～1，大小反映了街道内不同用地功能的混合程度.本研究选择居住、商业购物、商务办公与科教文卫用地的混合程度，利用Arc GIS平台的标识、合并等功能进行统计.计算公式为

(3)

式中：Hj为街道j内的土地利用混合度；Nj为街道j内用地类型数量；pij为第i类用地在街道j内的占比；n为用地类型总数.

商圈可达性采用“时间倒数的平方和”的形式表示，可以准确反映不同出行时间的商圈对居民的真实吸引力.其中，时间为高德地图路径规划API获得的驾车出行预计时间，商圈分别为钟楼商圈、南门商圈、小寨商圈、土门商圈、解放路商圈、高新商圈、龙首原商圈、经开商圈、三桥商圈、大兴商圈与康复路商圈.

通过上述方法得到各街道的企业密度、停车位密度等建成环境变量，对部分变量进行可视化(见图3)，并对上述10个自变量进行归一化处理，以降低量纲对模型的影响.

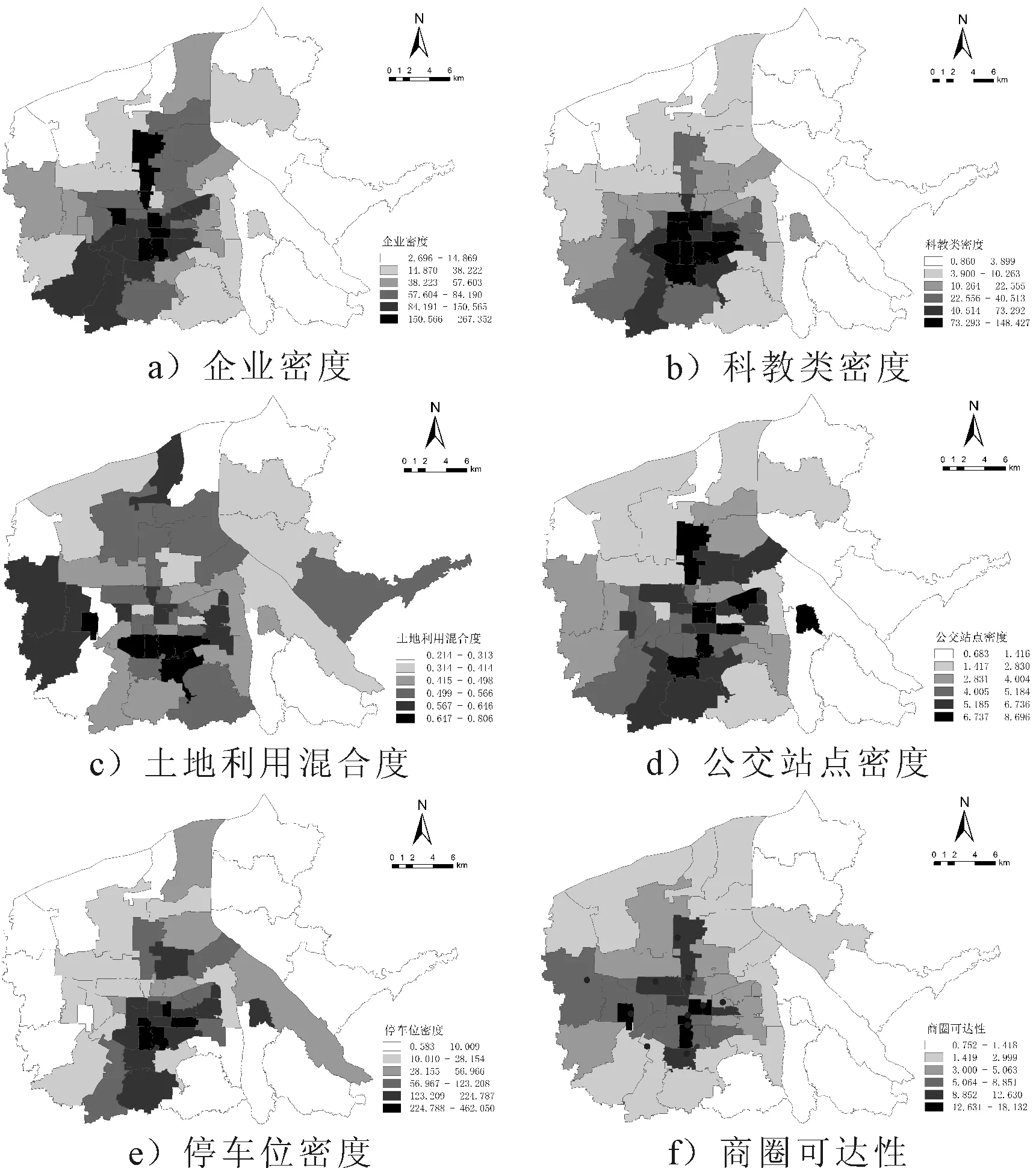
图3 建成环境变量的空间分布

2 地理加权回归模型

GWR模型中的参数是表示区域地理位置的函数，是对传统线性回归模型的改进，GWR模型主要优势为能够将空间权重矩阵运用在线性回归模型之中，很好地展现了结果的空间结构分异，公式为

(4)

式中：yi与xi1，xi2,…,xip为因变量y和自变量x1，x2,…,xp在样本点i(ui,vi)处的观测值；β0(ui,vi)为第i个样本点的常数项；βk(ui,vi)为第k个自变量在样本点i处的回归系数，εi为随机误差.

由于βk(ui,vi)参数随空间位置变化，因此将研究样本的空间相互影响转换为空间权重函数，利用加权最小二乘法进行参数估计，公式为

β(ui,vi)=[XTW(ui,vi)X]-1XTW(ui,vi)Y

(5)

式中：β(ui,vi)为第i样本点处的回归函数；X、Y分别为自变量与因变量；W(ui,vi)为包含距离函数的空间权重矩阵，高斯函数具有关于空间权重矩阵W连续且单调递减的优点，故选用高斯函数法作为权重函数，公式为

(6)

式中：wij为样本点i与样本点j之间的权重系数；dij为样本点i与样本点j之间的距离；b为带宽，是影响权重的关键因子.选择修正的AIC信息准则，对带宽进行优化，公式为

(7)

3 结果与分析

3.1 空间自相关分析

采用莫兰指数(Moran′s I)作为度量指标，以确定每个备选自变量的空间相关性，由表2可知，所有自变量的Moran′s I>0，P值<0.001，说明在99.9%的置信度下均存在空间自相关，此外，Z值均大于4，意味着自变量的空间分布均存在空间上聚集特征，故符合建立GWR模型的条件.

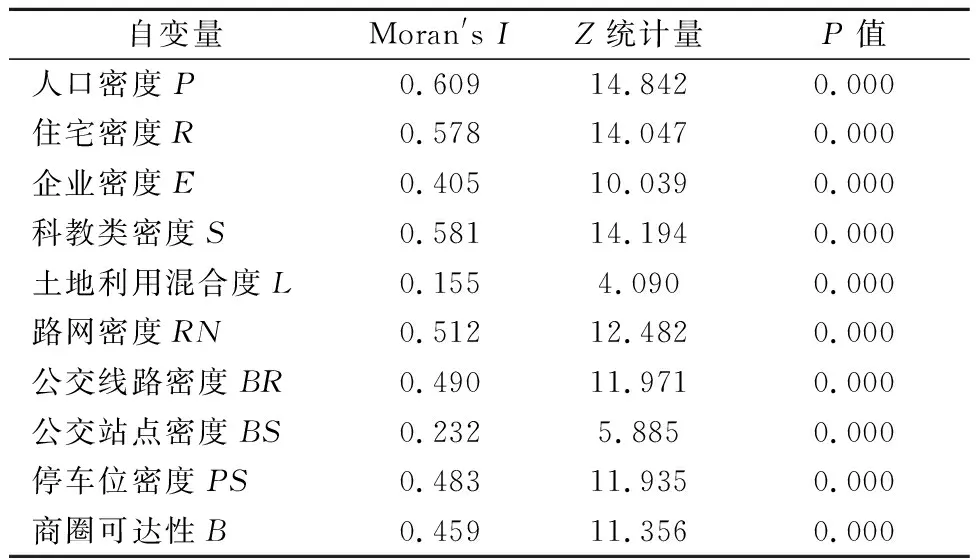
表2 Moran′s I测试结果

3.2 多重共线性检验

对备选自变量进行皮尔逊相关性分析，见表3.大部分相关系数都低于0.7，仅公交线路密度与路网密度、公交线路密度与公交站点密度、住宅密度与人口密度相系数大于0.7，相关性较高.采用方差膨胀因子(VIF)进行备选自变量的多重共线性检验，VIF越高，多重共线性的影响越严重，VIF>5时，认为自变量间存在较高的多重共线性.其中，公交线路密度(VIF=8.996)、住宅密度(VIF=7.623)、路网密度(VIF=5.796)与其他自变量之间存在共线性特征.剔除公交线路密度与住宅密度再进行共线性检验，剩余变量不存在多重共线性.

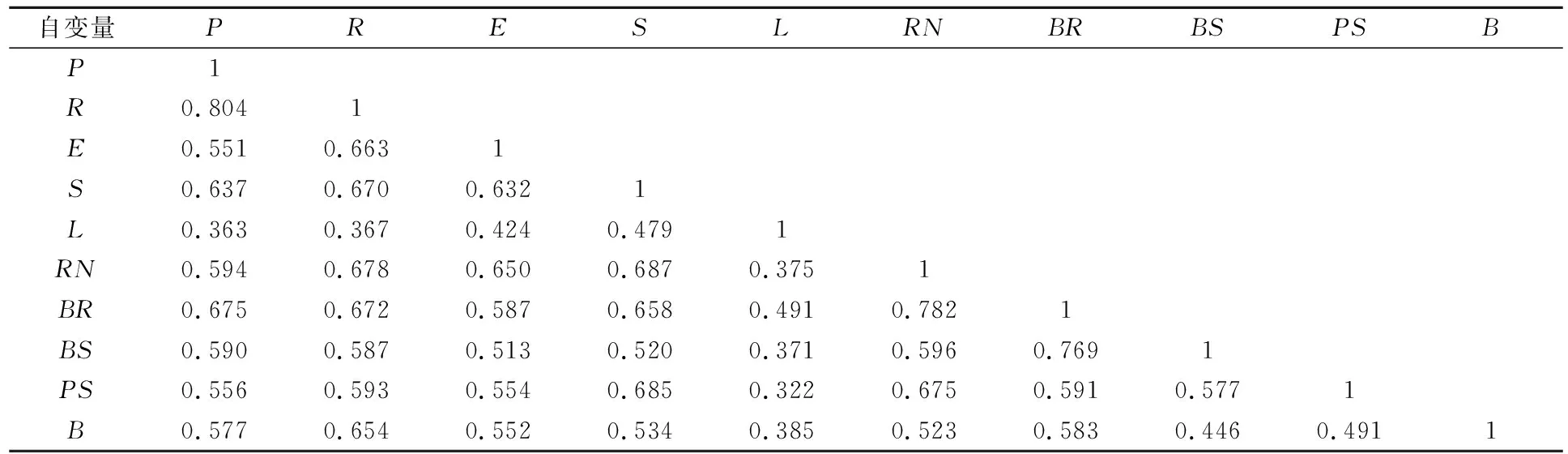
表3 备选自变量线性相关系数

3.3 地理加权回归结果分析

3.3.1模型对比

在测试和筛选了自变量后，采用OLS模型进行校准，以调查交通拥堵状态的显著影响因素.通过逐步回归，确定了人口密度、企业密度、科教类密度、土地利用混合度、公交站点密度、停车位密度与商圈可达性7个自变量P值低于0.05，说明上述7个指标具有统计显著性，对拥堵延时指数的影响较为显著，可进一步进行地理加权回归分析，回归结果见表4.

表4 OLS模型运算结果

在OLS模型进行全局回归基础上，基于Arc GIS平台运用GWR模型对拥堵延时指数影响因素的空间特性进行探究，见表5.由表5可知，GWR模型得出的校正后的R2值为0.776，与OLS模型相比有了显著提升；GWR模型的AICc值为8.014，低于OLS模型中的值，说明GWR模型能够更好地拟合观测数据.此外，GWR模型的标准化残差值也比OLS模型的小，且模型中各街道标准化残差值均<2.5，见图4.GWR模型相较于OLS模型在小寨路街道、长安路街道等地区残差相对减少，表明GWR模型准确性比OLS高.上述各项指标均证明GWR模型有更高的拟合度.

表5 GWR模型和OLS模型的比较

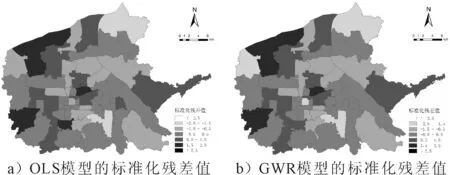
图4 OLS和GWR模型的标准化残差值空间分布

3.3.2影响因素的空间异质性分析

对GWR模型结果中各指标回归系数进行可视化分析，得到各指标系数的取值范围(绝对值)与空间分布图,见图5～6.

图5 GWR模型回归系数估计结果的变化范围

图6 地理加权回归模型回归系数空间分布

1) 人口密度的影响 人口密度与拥堵延时指数呈正相关.回归系数为[0.205～0.598]，影响程度呈现由东向西递减的趋势，回归系数高值主要集中在人口密度较低的席王街道(0.598)、灞桥街道(0.576)、纺织城街道(0.558)等区域，主要由于该地区属于城市外围，交通条件和基础设施建设较差，交通出行不便，居民出行对交通拥堵加剧产生影响较大.

2) 企业与科教类密度的影响 企业密度、科教类密度与拥堵延时指数呈显著正相关.企业密度回归系数为[0.405～0.553]，影响程度整体上呈现由内向外扩散性递减的圈层关系.科教类密度回归系数为[0.495～0.828]，对拥堵延时指数的影响程度表现出明显的东西差异，整体上呈现由西向东递减的趋势.企业与科教类密度影响程度较大的多为企业、科教类密集分布地区，主要是由于企业和科教类在空间上的过度集中，使该地区晚高峰出行量大，进而导致内部交通拥堵严重.

3) 土地利用混合度的影响 土地利用混合度与拥堵延时指数呈正相关.回归系数为[0.195～0.467]，回归系数高值主要集中在城区外围的洪庆街道(0.467)、灞桥街道(0.454)、丈八沟街道(0.432)等区域，是由于该地区土地利用混合度小，导致居民大规模、长距离的出行较多，对交通拥堵程度影响显著.碑林区太乙路街道、文艺路街道、张家村街道等区域土地利用混合度较大，可以减少居民通勤距离，使人更多选择公共交通、非机动车出行，能有效疏散晚高峰交通流量，对交通拥堵影响程度较小.

4) 公交站点密度的影响 公交站点密度与拥堵延时指数呈显著正相关.回归系数为[0.451～0.572]，影响程度整体上呈现由内向外扩散性递减的趋势，回归系数高值主要集中在公交站点密度相对较高的碑林区、新城区、莲湖区的街道，公交站点密度对市区影响要大于外围地区.这与一般认为的公共交通发展可以缓解交通拥堵不符，主要原因是公交站点高密度地区势必会产生大量的公交出行，干扰道路交通正常运行，进而导致交通拥堵加剧，也就是说盲目的增设公交站点不仅无法缓解交通拥堵，反而很大程度上会加大交通拥堵程度.

5) 停车位密度的影响 停车位密度与拥堵延时指数呈显著负相关.回归系数为[-0.788～-0.527]，即停车位的设置可以有效缓解交通拥堵.而碑林区与新城区的部分街道虽然停车位密度较大，但缓解拥堵效果却不及城市外围街道，①由于该地区大多为居住或者工作岗位聚集地，居民出行量大，导致缓解拥堵的效果不明显；②由于该地区部分街道停车位设置过多反而对缓解交通拥堵产生不利影响.

6) 商圈可达性的影响 商圈可达性与拥堵延时指数呈负相关.回归系数为[-0.554～-0.333]，影响程度整体上呈现由西向东递减的趋势，主要是由于碑林区、新城区与莲湖区交通拥堵受其他因素影响较大，且电子城街道、丈八沟街道企业密度较大，人口密度较小，职住分离会引发大规模、长距离的通勤交通需求，使得该地区可达性水平与交通拥堵程度有较强的相关性.

总体来看，7个自变量的回归系数在地理空间上存在明显的非平稳性，企业密度与公交站点密度对拥堵延时指数的效应差异整体较小，其余变量的影响程度偏差较大，介于0.2～0.4.各指标对于拥堵延时指数的影响能力和影响效应有所不同，进一步证明了影响因素的空间异质性.

4 结 论

1) 交通拥堵状态影响因素存在空间异质性GWR模型结果表明，人口密度、企业密度、科教类密度、土地利用混合度、公交站点密度与拥堵延时指数呈正相关，停车位密度、商圈可达性呈负相关.人口密度、科教类密度、土地利用混合度、停车位密度与商圈可达性对拥堵延时指数的影响呈现出明显的空间异质性，企业密度与公交站点密度对拥堵延时指数的效应差异整体较小.从影响程度上来看，科教类与停车位密度对交通拥堵状况的影响最显著，其次是公交站点密度、企业密度、商圈可达性与人口密度，土地利用混合度的影响强度相对较小.

2) GWR模型相较于OLS模型，拟合优度由0.721提高到0.776，GWR模型拟合效果更好，能够很好地解释交通拥堵状态.证明了GWR模型对于分析交通拥堵状态与建成环境关系具有独特的空间异质性和尺度依存特性优势，有助于消除由空间异质性产生的潜在偏差，解决了传统方法无法在空间上分析交通拥堵状态相关因素的空间差异性问题.

由于数据的局限性，本文影响因素选取还不够全面，且并未涉及影响因素在时间尺度上的空间差异.接下来考虑从时间和空间两个层面进行探究，全面分析交通拥堵状态影响因素的时空异质性，为各地区制定不同尺度的交通拥堵治理对策提供依据.