基于LSTCN模型的城市交通速度预测

殷仕山 孙克雷

(安徽理工大学计算机科学与工程学院 淮南 232001)

0 引 言

由于挖掘时空模式的强大能力，在交通预测领域中越来越多地采用基于深度学习的方法[1].Lyu等[2]提出了一种基于深度学习的堆叠式自动编码器(SAE)模型，以捕获交通流量预测中的时空相关性.Koesdwiady等[3]结合了DBN和决策级数据融合方案来同时预测交通流量和天气状况.Kuremoto等[4]研究了如何将基于受限Boltzmann机的深度置信度网络应用于短时交通速度预测.Ma等[5]运用长期短期记忆(LSTM)来捕获交通速度预测的长期时间特征.然而，LSTM每次只读取和分析输入序列中的一个速度值.循环神经网络必须等待前一个速度值处理完毕后才能处理下一个值，这意味着循环神经网络无法像CNN那样进行大规模并行处理，而传统的神经网络无法精确提取数据的时间特征，所以对时间序列的研究又转向了卷积神经网络.

卷积神经网络CNN在处理二维数据(如图像)时表现良好，通常由卷积层和下采样层叠加而成，即池化层.Wang等[6]提出了一种基于单隐层卷积神经网络结合误差反馈的交通流速度预测模型.Yu等[7]提出了一种基于卷积神经网络的数据分组模型，该模型由两部分组成.连续词模型(CBOW)用于寻找相似的时空关系，而CNN网络用于短期速度预测.Ma等[8]将时空交通速度矩阵转换为图像，然后将其作为CNN的输入，用于交通速度预测.罗文慧等[9]考虑到天气，事故等异常情况，利用CNN提取交通流的时空特征，输入到顶层SVM模型中进行预测.Wu等[10]通过使用一维CNN来利用空间特征和两个LSTM来表征交通流的时间相关性来预测交通流.Ke等[11]运用融合卷积LSTM(Conv-LSTM)来开发时空深度学习模型，以预测按需乘车服务下的乘客需求.从以上的CNN文献中发现，传统的CNN只能在滑动窗口有限的情况下提取局部信息.结果，当提取过程数据的深层特征时，CNN可能仍然会遇到梯度消失的问题.为了解决此问题，专门开发了时间卷积网络(temporal convolutional network，TCN)以处理序列建模问题.

利用CNN和RNN的优势，TCN具有以下三个特征来改进时间序列建模的性能：因果卷积，扩展卷积和残差连接.因果卷积在输入和输出之间建立了牢固的因果关系；扩张的卷积增加了TCN的接收场，而无需使用太多的隐藏层；残差连接功能避免了梯度消失的可能性.文中首先将交通速度数据建模为时间序列问题，然后提出了一种预测城市交通速度的长短期时间卷积网(long and short-term temporal convolutional network，LSTCN)模型.LSTCN预测模型对时间卷积网络进行了改进，使其能捕捉交通速度序列特征，并充分考虑天气因素对交通速度的影响，从而更准确地预测城市交通速度.

1 交通速度与天气因素的研究

1.1 交通速度的时间特征

道路交通速度数据在短期内具有明显的趋势性，在长期内具有周期性特征[12],见图1.对深圳市罗湖区2015年1月20日、周二10:00—10:15的交通速度进行预测，那么当天09：00—10:00内的交通数据以及对应的周一10:00—10:15和上周周二10:00—10:15的交通速度数据将为预测提供最有用的信息，而当天06：00点的交通情况通常与预测目标无关.

图1 交通速度数据周期性

由图1可知：13日、19日和20日的速度趋势变化非常相似，说明了交通速度数据存在明显的日周期性和周周期性.

1.2 天气因素的处理

天气的变化会直接影响交通速度的变化[13].通过世界气象在线网站的接口，获取所需城市的气象数据，并选取10个可量化的气象参数作为外部数据特征.由于天气因素与道路交通速度之间的作为具有复杂的非线性关系，采用皮尔逊(Pearson)相关系数来度量10个天气因素与交通速度之间的相关性.分析结果见图2.

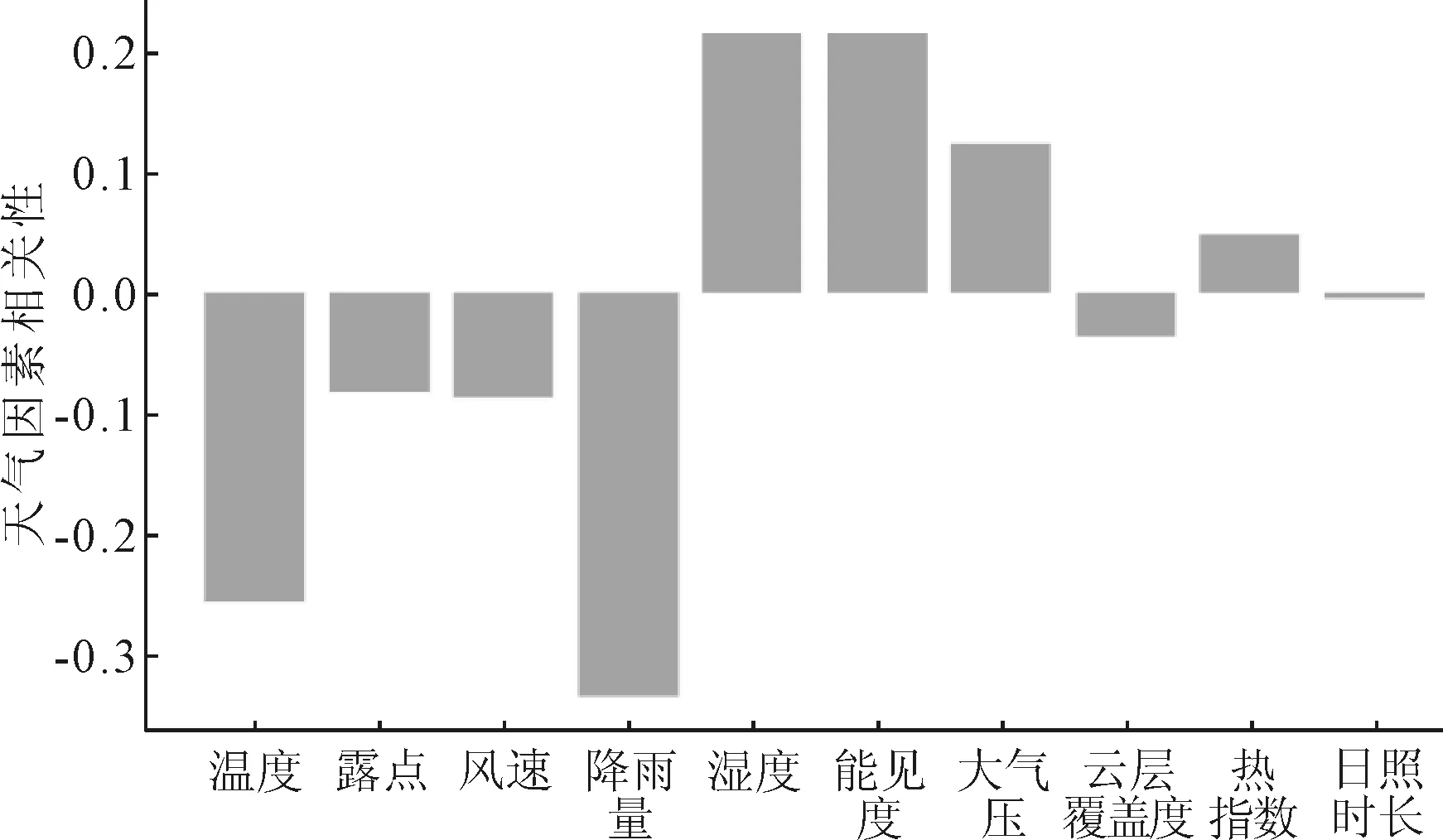
图2 天气因素相关性

气象特征数据与交通速度数据的相关系数为

r(xw,yt)=

(1)

式中：n为采样点数据的个数；xw为归一化后的气象特征数据；yt为降采样以及归一化后的交通速度数据；r(xw,yt)为气象特征数据与交通速度数据之间的相关系数[14].相关系数r的值在[0，1]之间，r越接近1，关联度越强，r越接近0，关联度越弱.r(xw,yt)的绝对值反映了天气数据与交通数据的关联度.本文选取相关系数超过0.2的影响因子，即温度，降雨量，湿度和能见度，以缩小选取的时空范围，削弱低于此标准的影响效应.

2 长短期时间卷积网络模型

2.1 时间卷积网络

TCN是一种特殊的1D-CNN，用于时间序列预测和分类任务，TCN在多种任务和数据集上的性能优于LSTM、GRU等典型的递归神经网络，相比于递归神经网络，TCN可以记住更长的历史信息，捕获更全局的时间序列特征.

为了实现对长期历史尺度输入的有效预测，不论是使用深层次的网络还是大量的卷积核，都需占用大量的计算资源，并且时空复杂度很高.因此引入了扩展卷积机制，使得模型能够用更小的滤波器和更浅的网络层覆盖更大的时间序列范围.

对于一维输入序列I∈Rs和卷积核F:{0,2,…,k-1}→R，对序列元素x的扩展卷积运算F定义为

(2)

式中：d为扩展间隔；k为卷积核的大小，因果扩展卷积的示意图见图3.

图3 三层因果扩展卷积网络

时间卷积网络中还加入了残差连接、权值归一化和dropout来提高性能，一个完整的TCN残差块见图4.

图4 时间卷积网络

2.2 融合天气因素的LSTCN交通速度预测模型

考虑到交通速度数据同时具有短期趋势性和长期周期性，本文类比长短期记忆网络模型的思想，提出了一种长短期卷积网络.交通流数据预测遵循因果关系原则，但不需要连续不间断的历史数据输入.例如，10：00的交通流量与06：00的交通流量并不相关，因此扩展间隔的设计不需要覆盖所有的序列范围.

以Q次/h为研究对象的统计频率，设当前时间为T0，待预测的数据点为Tp,在此时间序列上分别截取近期趋势Tn，日周期Td和周周期Tw，充分提取交通速度数据的时间特征，见图5.

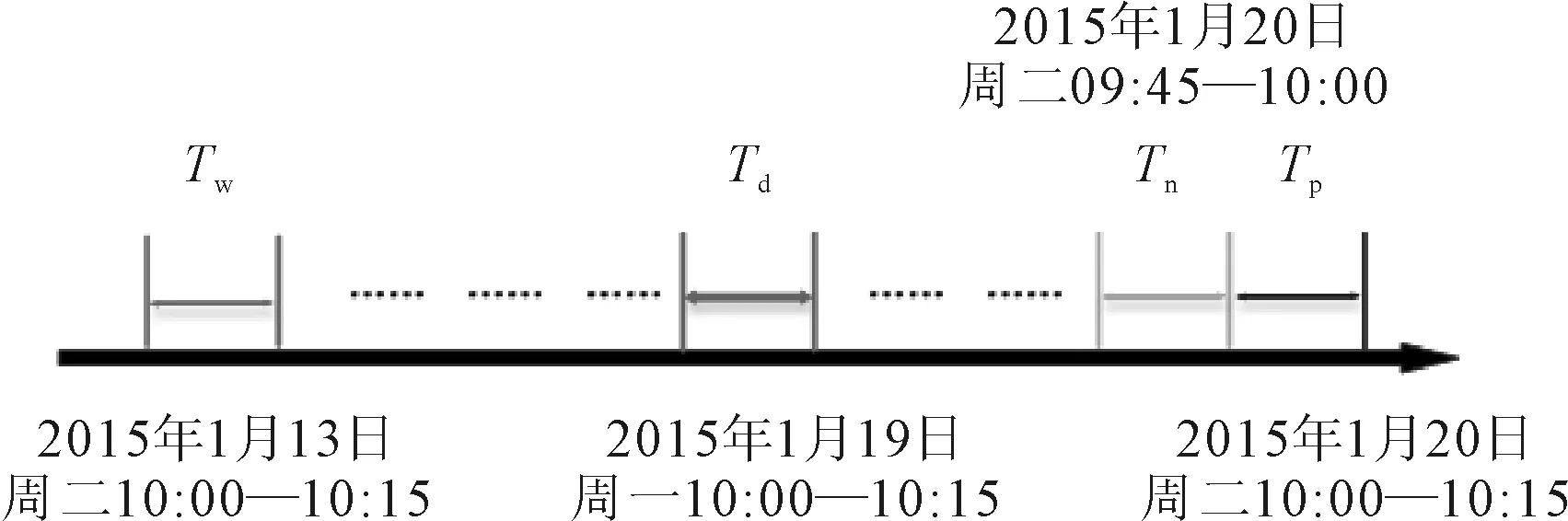
图5 交通速度时间特征示例

1) 近期趋势性Xn=(XT0-Tn+1,XT0-Tn+2,…,XT0)，即与预测目标数据紧邻的历史时间序列，见图5中Tn段.城市道路上车辆的汇集和分散是渐变式的，同一地点前一时刻的车流量势必会影响下一时刻的车流量，进而影响交通速度的变化.

所有时间序列预测模型都要求网络的输入输出长度相等并且序列中任意时刻T对应的节点只接受T时间之前的信息.LSTCN在网络输出端用了全连接层来保证输出序列与输入长度相等，继承了时间卷积网络中采用的具有因果关系的卷积来保证网络中的任一时间节点在模型的各阶段只获得历史时刻的信息,见图6.

图6 基于长短期时间卷积网络的预测模型

模型首先对交通速度和气象特征的近期趋势性进行特征提取，经实验得出使用3层TCN效果最佳.其次提取交通速度的周期性特征，将TCN扩展间隔设置为D、W，分别代表每日和每周的时间序列长度.最后将二者提取的特征统一维度后相加，经过全连接层输出预测结果Pi，简单表示为

Pi=TCN5level(Xtra)+TCN3level(Xwea)

(3)

具体预测流程如下.

步骤1将交通速度序列数据以滑动窗口的方式进行处理，窗口大小为12，每次向前滑动一个数据，即时间特征数目为12，预测下一个时刻的交通速度.

步骤2筛选出相关性最强的四个气象特征，将气象特征序列直接作为辅助特征.

步骤3对滑窗处理后的交通速度数据和气象特征数据进行预处理并划分训练集与测试集.

步骤4将训练集输入LSTCN模型进行训练.

步骤5用训练好的模型预测测试集交通速度大小，使用常用的评价指标计算误差.

3 实验与评估

3.1 数据来源与预处理

广州道路交通速度数据(GZ):由214个匿名路段(主要是城市快速路和主干道)组成，数据采集间隔为10 min.实验选取2016年8—9月的数据，其中，前50 d的数据用于训练，后11 d的数据用于测试.深圳道路通行速度数据(SZ):由罗湖区156条主干道组成，数据采集间隔为15 min.实验选取2015年1月1—31日的数据，其中，前24 d的数据用于训练，后7 d的数据用于测试.

对交通速度和筛选后的气象特征数据进行归一化处理,对数据使用了离差标准化，是对原始数据的线性变换，使结果值映射到[0～1]，公式为

(4)

式中：x为交通速度和气象特征的原始数据；y为处理后的数据；xmax为原始数据集中的最大值；xmin为其最小值.

3.2 模型评价指标

选取回归问题最常用的四个评价指标，即平均绝对误差(MAE)，均方误差(MSE)，均方根误差(RMSE)和平均绝对百分比误差(MAPE)对交通速度预测模型进行评价.四个指标的定义为

(5)

(6)

(7)

(8)

式中：N为预测值的个数；Pi为观测点的预测交通速度值；Fi为对应的真实交通速度值；MAE，MSE，RMSE，MAPE的值越小，表明模型的预测精度越高.

3.3 实验环境和参数设置

3.3.1TCN隐层节点数的确定

隐层节点数是决定模型提取数据特征能力的重要参数，太少的节点数意味着网络性能较差；过多的节点数虽然能够减小网络的系统误差，但是会延长不必要的训练时间，甚至出现过拟合.考察了不同隐层节点下模型的预测误差，结果见表1.由表1可知：模型的预测误差随节点数的增加而变化，根据实验结果，将TCN隐层节点数设置为64.

表1 不同TCN隐层节点数实验结果对比

3.3.2周期性中TCN卷积核大小的确定

为了探究不同周期性数据的输入长度，即TCN卷积核的大小对预测结果的影响，在广州数据集进行了参数实验，考虑到模型的运算效率问题，将卷积核大小分别设置为Td={2，3，4}，Tw={2，3，4}，部分结果见表2.根据结果，最终确定卷积核大小为{3，3}.

表2 不同TCN卷积核大小实验结果对比

3.3.3近期趋势性中TCN层数的确定

对TCN的层数进行实验验证，验证结果见表3.由表3可知，模型的预测误差随着TCN层数的增加呈现先下降后上升的趋势，因为层数越多参数量越大，反而难以训练，为了使模型能够达到最佳性能，最终确定使用三层的TCN.

表3 不同TCN层数实验结果对比

3.3.4其他参数

提取周期性特征的后两层的扩展间隔为每日和每周包含的时间节点数量，深圳数据集的扩展间隔为{1，2，4，96，672}，广州数据集的为{1，2，4，144，1 008}.综合考虑精度和效率要求，将训练Epoch设置为500次，批量规模为128，使用了学习率衰减和Adam优化.

3.4 实验结果与分析

首先比较了LSTM、GRU、TCN和未考虑天气因素的LSTCN四种深度学习模型的预测结果.LSTM和GRU采用了常规的三层结构，TCN则使用了和本文模型近期趋势性相同的三层结构，便于对比.为保证实验公平性，上述模型使用相同的交通数据特征输入，以及统一的Adam优化器.

为了清楚地比较四种深度学习模型的预测性能，展示了广州和深圳的预测数据，见图7.四种模型都能较好地拟合真实数据，与LSTM，GRU和TCN模型相比，LSTCN对速度变化趋势的拟合程度要明显优于其他模型.具体来说，在深圳数据集上，它的整体预测值偏低，对变化的大趋势预测精准；在广州数据集上，拟合效果更加优秀，特别是在数据突变处.

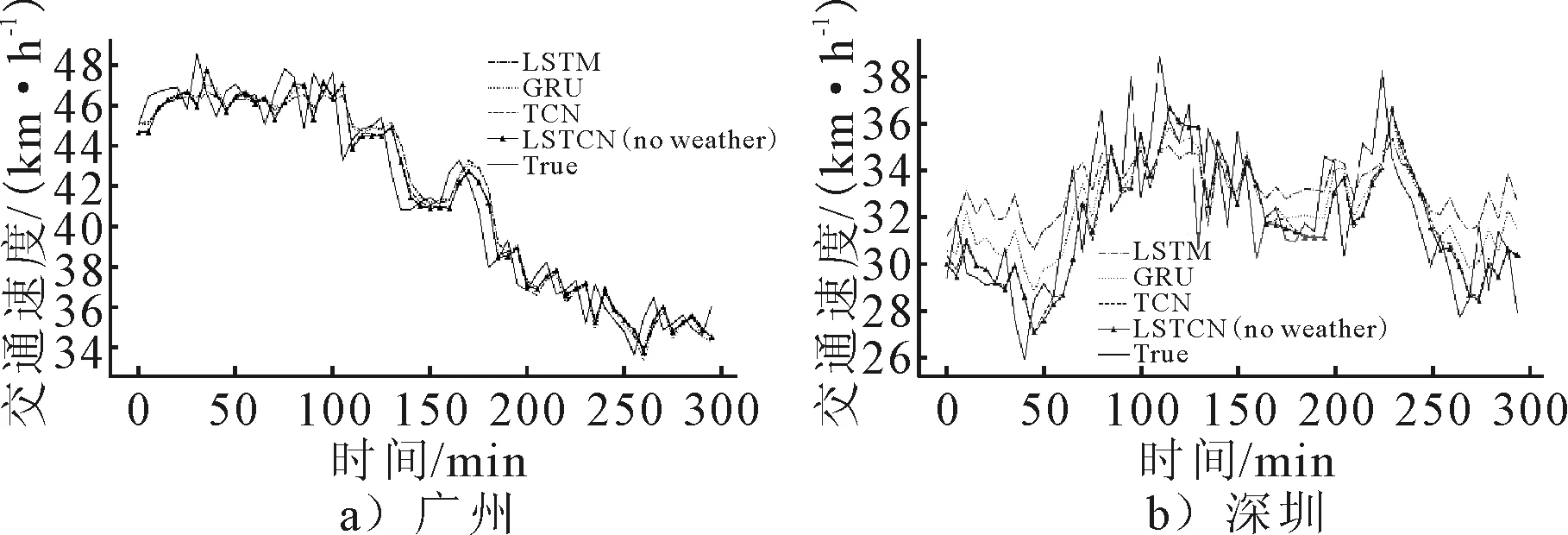
图7 模型预测结果对比

为了保证预测结果的稳定性，进行了多次实验，得到的各项测试误差平均值见表4.在本次实验中，TCN的性能优于LSTM和GRU，LSTCN取得了最好的效果.与LSTM模型相比，在广州数据集上的MAE降低了5.4%，RMSE降低了3.5%，MAPE降低了0.21%.

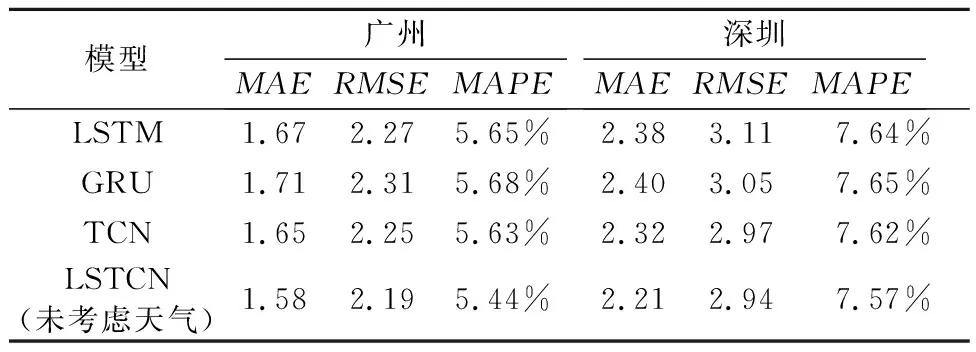
表4 模型预测性能比较

图8为测试集在训练过程中的均方误差MSE的变化曲线，可以看出训练开始时TCN和LSTCN的收敛速度明显快于LSTM和GRU，后续训练过程相差不大，都是在抖动中缓慢下降.LSTM和GRU都属于循环神经网络RNN模型的变种，所以每个单元的训练都需要等待前一个单元的输出，导致每次训练所消耗的时间是卷积神经网络的数倍，因此在相同epoch次数下LSTCN的实际收敛时间比LSTM和GRU要低，但要高于模型更简单的TCN模型.

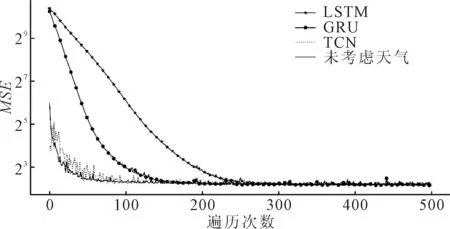
图8 测试集MSE在训练过程中的变化

为了进一步说明天气因素对交通速度预测的影响，验证预测模型的有效性，分别用未融合天气因素的LSTCN预测模型和融合天气因素的LSTCN预测模型对两个城市的交通速度做了预测，并通过常用误差评价指标对预测结果做了对比，结果见表5.

表5 融合天气因素前后预测性能比较

由表5可知，融合了天气因素对城市交通速度预测时的各项误差都要小于单靠交通速度数据进行预测时的误差，提高了预测精度.由此可以得出，融合天气因素之后，有效地改善了交通速度预测效果，说明了天气因素确实会影响城市交通速度的预测，从而验证了预测模型的可行性.

4 结 束 语

针对天气因素对交通速度的影响以及现有方法在超长时间序列预测精度上的不足，提出一种基于综合天气因素的长短期时间卷积网络的交通速度预测模型LSTCN，用于综合捕捉交通流的时间特征和外部天气特征.长短期时间卷积网络可以并行处理时间序列，相比常用的循环神经网络，训练速度快，占用内存少.通过反复试验确定预测模型的参数，并与常用的时间序列预测方法进行比较，结果证明我们的预测精度和运算效率较高.但本文没有考虑空间特征对预测结果的影响，今后将利用图卷积结构对模型进行改进.