地铁网络节点的聚类分析与关键节点识别

薛 锋 刘泳博 施 政 户佐安* 何传磊

(西南交通大学交通运输与物流学院1) 成都 611756)(西南交通大学综合交通大数据应用技术国家工程实验室2) 成都 611756)(西南交通大学唐山研究生院3) 唐山 063000) (中铁第一勘察设计院集团有限公司4) 西安 710043)

0 引 言

城市轨道交通网络对城市公共交通系统具有重要支撑作用，网络节点的畅通与否会影响城市轨道交通网络的通行效率，严重时甚至会导致网络的瘫痪.因此，对城市轨道交通网络的关键节点进行有效识别，找出重要的“核心节点”，并通过重点保护这些“核心节点”提高整个地铁网络的可靠性，有助于提升网络的运营安全和效率.

目前，对于城市轨道交通网络关键节点识别的研究较多，大都是在复杂网络节点重要度评估方法基础上进行扩展，使用节点度、介数等指标对节点进行评价.Yang等[1]认为节点的重要度取决于度和介数两个指标，但多个指标反映的结果往往不同，需要对多指标结果进一步分析，以得到更加完善结果.在这一过程中，有学者使用PageRank[2]、灰色关联法[3]、TOPSIS[4]等方法对网络节点的多个指标进行分析，得出节点重要程度的排名，但评价模型往往涉及多指标权重确定，这一环节的存在导致评价结果存在较大主观性；其次在得出网络节点重要度排名后，往往采用人为规定阈值的方法确定关键节点，主观性较强，而使用聚类方法可以避免主观因素对网络关键节点识别的影响.蚁群聚类算法具有鲁棒性、稳健性的特点，在实际应用中比较广泛[5-7]，但蚁群聚类算法存在收敛慢，易陷入局部最优的缺点[8].

基于此，文中采用聚类分析的方法，根据评估节点重要度的指标对地铁网络节点进行分类，并构建了网络关键节点识别的模型，采用改进的蚁群聚类算法对模型进行求解.选取最大连通子图和网络效率这两个指标，分析不同节点类被随机攻击时网络性能的下降趋势，为地铁网络节点的维护提供参考.

1 地铁网络关键节点识别指标

评估网络节点重要度的指标有很多，一般是从节点的度、介数、连通度等拓扑结构或脆弱性指标进行衡量[9]，但是地铁网络的节点重要度评估还需结合地铁网络的实际情况，不仅要反映节点在网络中的重要性，还应体现车站周边的经济水平以及集散旅客、连接其他交通方式的能力.因此，根据已有的资料并结合文献[4]和文献[9]，选取识别地铁网络关键节点的指标，见图1.

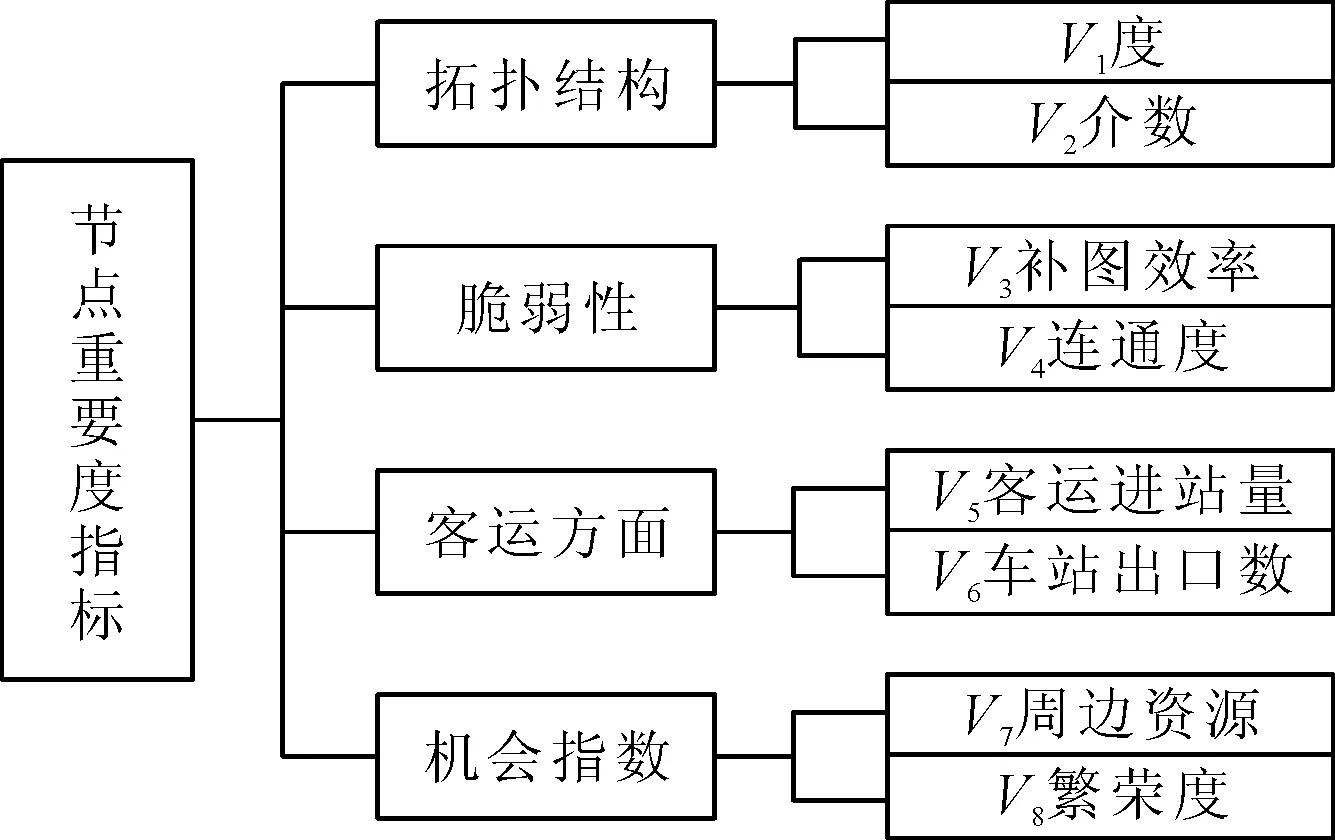
图1 关键节点的识别指标

V1度，V2介数，V3补图效率和V4连通度等指标根据文献[4]中的公式计算所得，V5客运进站量用某一时间段内的日平均进站量计算所得，V7周边资源根据地铁站周边的学校、医院、商业街等资源评估所得，V8繁荣度则选择车站所属地区的人均GDP统计所得.

2 聚类识别关键节点类的原理及算法

地铁网络关键节点的识别可以采取聚类思想，通过将相同或相近属性节点进行归纳[11-12]，将地铁网络关键节点找寻问题转化为聚类问题来解决，其结果既能揭示不同类别的网络节点内部的隐含关系，又能通过进一步的分析找出地铁网络中的关键节点类.

2.1 聚类分析进行关键节点类识别的原理

通过聚类来进行网络关键节点识别的原理可以描述为：将地铁网络中的节点看作m维空间Rm中的n个向量(数据集)，把每个向量归属到K个聚类中的某一个，使每个向量与其聚类中心的距离最小，然后计算每个簇的类别中心值，中心值最大的那个簇即为网络中的关键节点类，其数学模型描述如下所示：

已知地铁网络节点集X有n个节点和K个分类，每个节点有m个属性，由此得到节点集矩阵为

(1)

将节点集中的n个节点进行聚类，在聚类过程中引入0-1决策变量wij，当节点Xi在j类节点S(j)中取值为1，否则取值为0，则有：

(2)

以每个节点与其聚类中心的距离最小为目标函数，构建网络节点聚类的数学模型为

(3)

(4)

(5)

(6)

当JE最小时，聚类效果达到最佳.此时，类别中心值最大的簇即为关键节点簇，数学表达式为

(7)

(8)

2.2 关键节点识别的算法

蚁群聚类算法是一种基于蚂蚁觅食行为的仿生算法，具有鲁棒性强的优点，但是也存在容易陷入局部最优，在指定迭代次数的条件下很难找到最优解的缺点.

为了更好地运用蚁群聚类算法解决地铁网络关键节点的识别问题，需要对传统的蚁群聚类算法进行改进.本文结合遗传算法中的变异思想，对蚁群聚类算法进行改进，改进后的算法流程如下.

步骤1初始化算法的参数.

步骤2确定初始解.根据信息矩阵中信息素的值和状态转移概率确定蚂蚁行走路径，并进行标识，方法如下.

(9)

式中：pij(t)为蚂蚁在第t次聚类过程时从数据Xi与Xj的状态转移概率；τij(t)为蚂蚁在第t次聚类过程时从数据Xi与Xj产生的信息素；q为直接转移阈值.

步骤3确定聚类中心.根据路径标识得到当前聚类中心，计算所有样本到对应聚类中心的偏差量JE.

步骤4对路径进行变异操作.对JE_min所对应的路径进行变异，并计算该路径下所有样本对应聚类中心的偏差量JE_new.若JE_new小于JE_min，则将变异后的路径作为下一次迭代中蚂蚁选择的路径，反之则返回原路径.

步骤5更新信息素.每次聚类完成后，将所有的蚂蚁产生的路径按偏差量升序排列，同时更新路径上的信息素浓度；信息素按比例rho挥发，而偏差量较小的L个蚂蚁对其所在路径产生增量.信息素的更新公式为

(10)

步骤6重复步骤3～6，直到偏差量JE稳定或者达到最大迭代次数为止.

步骤7关键节点识别.比较各节点类的类别中心值，将类别中心值最大的节点类确定为关键节点.

3 实例分析

选取文献[4]中成都地铁网络节点的数据进行仿真实验，截至到2018年4月，成都地铁共计6条线路，136个站点，整个城市轨道交通网络呈“井+环”形，可以视为线路与站点构成的复杂网络，其各节点编号及网络拓扑图见图2.

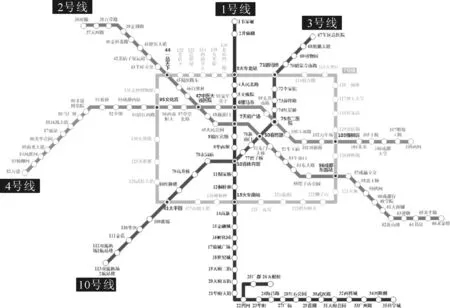
图2 成都地铁线路图(2018年4月)

3.1 网络关键节点识别前的准备

1) 数据预处理 为了提升实验结果的精度，需对各指标的数据进行标准化处理.采用归一化方法对成都地铁网络中的136个站点和8个属性数据进行归一化处理，计算公式为

(i=1,2,…,136;j=1,2,…,8)

(11)

2) 最佳聚类簇数的确定 前文设计的蚁群聚类算法的聚类簇数K需预先设定，为了找出合适的K值，结合文献[12]，选取样本聚类误差平方和(SSE)指标作为最优聚类K确定的依据.SSE计算公式为

(12)

式中：K为聚类的簇数；p为聚类的样本；mk为第k类的聚类中心.SSE随着K的变大而逐渐变小，当K越大，此时SSE则越小，说明样本的聚类效果越好.当K比真实的聚类簇数小时，K的增大会大幅降低聚类的效果，所以SSE也会大幅下降，当K为真实的聚类簇数时，SSE下降的趋势会大幅减小，然后随着K值的不断增大而渐渐趋于平缓，而使SSE最先趋于平缓的K值就是最佳的聚类簇数.因此，本文将预处理后的数据按照不同的K值进行聚类，得到SSE-K的趋势图，见图3.

图3 SSE-K趋势图

根据图3可以确定出在K=3时，曲线最先趋于平缓.因此，成都市地铁网络节点聚类分析问题的最佳聚类簇数K为3.

3.2 聚类性能检验及结果

3.2.1聚类性能的检验

分别用传统蚁群聚类算法与改进的蚁群聚类算法将预处理后的136个站点的8个属性指标的数据进行聚类，算法的参数设置如下：蚂蚁数R=1 000，最大迭代次数t_max=3 000，转移阈值q=0.9，变异率pls=0.1，局部寻优路径L=2，信息素系数c=0.01，信息素挥发率rho=0.1.利用Matlab编程得到两种算法偏差量的收敛曲线，结果见图4.

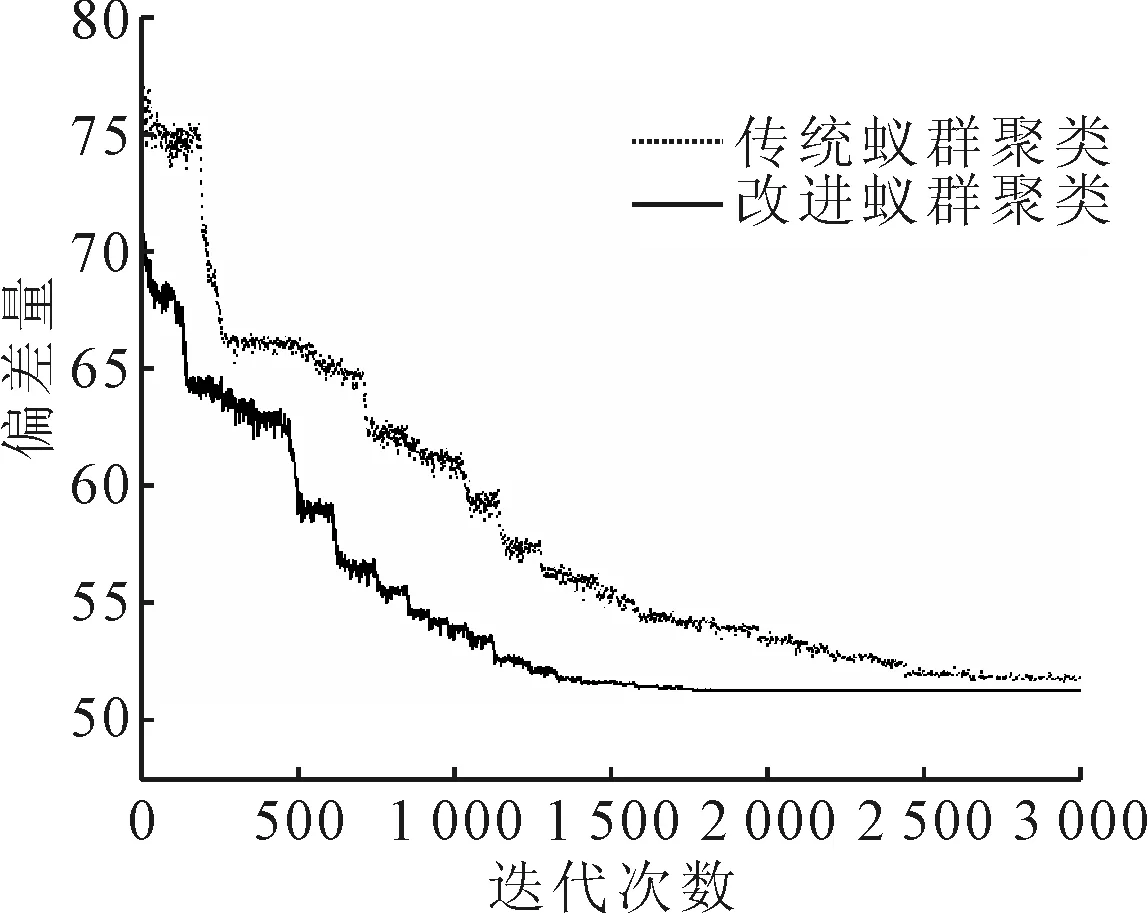
图4 偏差量的收敛曲线

由图4可知，传统的蚁群聚类算法在迭代3 000次以后收敛，而改进的蚁群聚类算法在迭代了1 600次的时候曲线收敛，其收敛的速度明显更快，而且两种算法在CPU为inter i7-8700K、内存为32 G的计算机每聚类一次，运行时间均在0.3 s左右.因此，从效率而言，改进的蚁群聚类算法，相较于传统的蚁群聚类，运行效率提升了近1倍.

3.2.2聚类的结果

通过改进的蚁群聚类算法得到成都市136个地铁站点的最佳聚类结果见表1.由表1可知:聚类结果与实际情况十分吻合，如：类别1中的站点，如韦家碾、广州路、双流机场等71个站点在地铁线路中多为规模较小的中间站；类别2中的站点，如文殊院、锦江宾馆、惠王陵等39个站点在地铁线路中多为规模较大的中间站；类别3中的站点，如火车北站、天府广场、成都东站等26个站点在成都的地铁网络中多为规模大的换乘站，这些站点多分布于成都经济较为发达、人口密度大的区域，在整个地铁网络的运营中承担了重要角色.

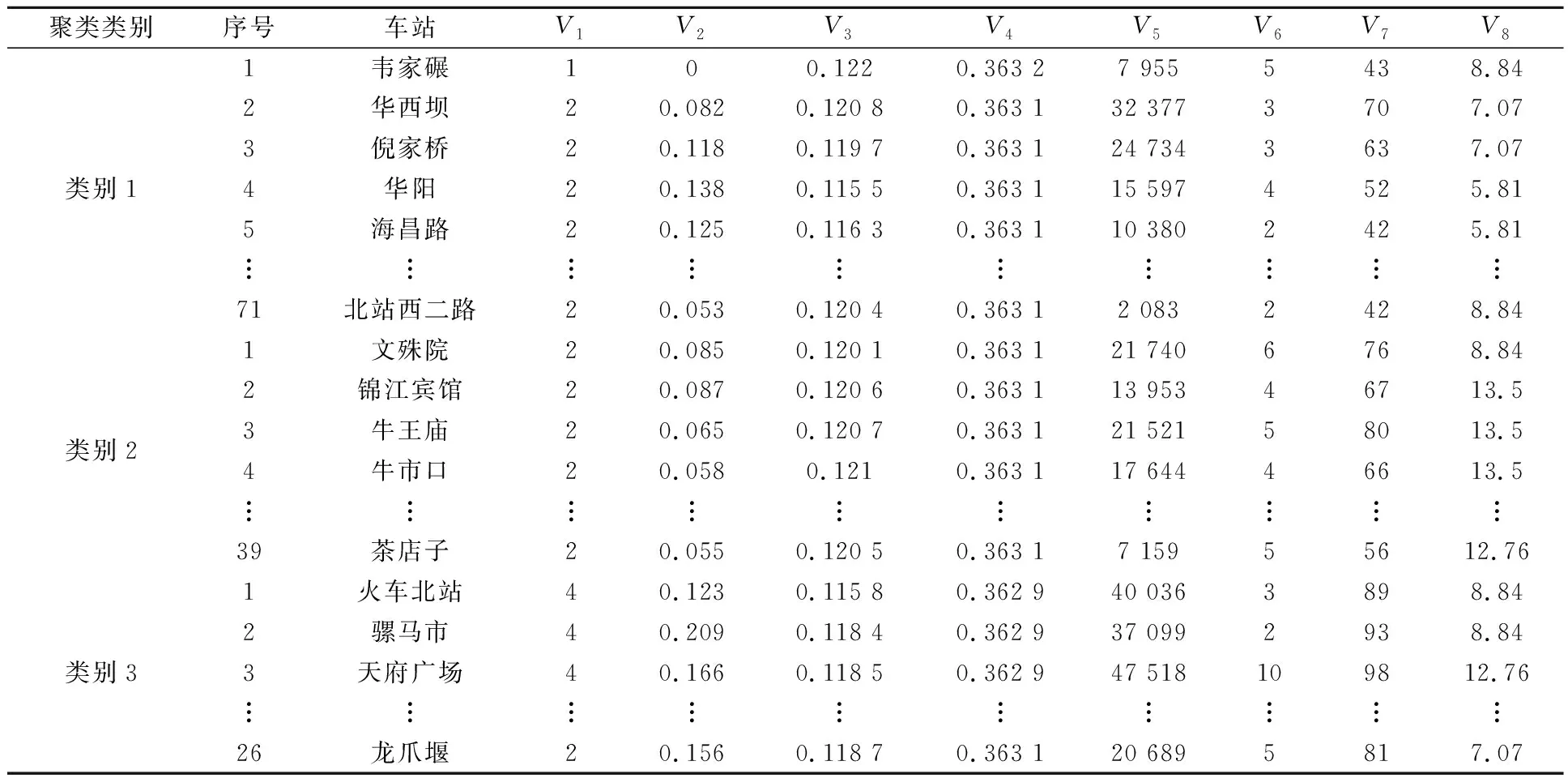
表1 聚类结果

3.2.3网络关键节点的识别

结合3.2.2中聚类结果可计算得类别1、类别2、类别3的聚类中心及类别中心值见表2.按照类别中心值的大小排序为：类别3>类别2>类别1，因此可以判断出类别3的节点为地铁网络中的关键节点.该结论与文献[4]中运用灰色关联和TOPSIS加权评价识别出的关键节点一致，从而验证了改进的蚁群聚类算法在地铁网络关键节点识别中的有效性和准确性，同时也减少了传统评价模型在识别关键点过程中主观因素的影响.

表2 聚类中心及类别中心值

3.3 随机攻击下的网络的鲁棒性分析

3.3.1网络鲁棒性的衡量指标

参考文献[13]，选取网络效率、最大连通子图

两个指标来描述节点损坏后网络性能的变化.其中，网络效率反映网络的效用情况，计算公式为

(13)

式中：dij为节点i,j之间的最短路径.

最大连通子图的大小指网络被攻击后被分成若干网络，其中包含节点最多的图为最大连通子图，它反映了地铁网络的抗毁性，计算公式为

J=N′/N

(14)

式中：N′和N分别为损坏前后的最大连通子图的大小.

3.3.2随机攻击对网络鲁棒性的影响分析

根据前文中对节点进行的聚类处理，观察不同类的节点在随机攻击下失效而影响地铁网络性能变化的程度，具体步骤如下.

步骤1分别将类别1、类别2、类别3中的节点作为首先攻击的对象，对每一类的节点随机攻击，即随机地不断移除节点.

步骤2计算移除节点后的网络性能指标.

步骤3绘图分析，得到相关结论.

按照上述步骤，依次损坏网络中的节点，破坏地铁网络的连通性.默认初始性能为100%，对三种节点类中的节点依次随机攻击，并分析网络性能的下降态势与被攻击节点间的关系，见图5.

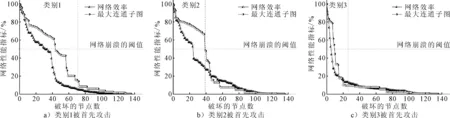
图5 随机攻击下网络性能的变化

根据文献[14]，网络崩溃的临界值为初始性能的50%，结合网络崩溃的临界阈值，对网络的鲁棒性进行分析.由图5可知：类别1中的节点被率先随机攻击时，当有27个节点被攻击时，网络效率下降到70.9%，最大连通子图下降到54%；类别2中的节点被率先随机攻击时，当同样有27个节点被攻击时，网络效率下降到39%，最大连通子图指标下降较慢，此时为73%；类别3中的节点被率先随机攻击之后网络效率和最大连通子图会急剧下降，当有9个节点被破坏时，网络效率和最大连通图分别下降到28%和45%，整个网络近乎瘫痪.

通过图5的比较分析，可知类别1中的节点被破坏对最大连通子图的影响较大，对网络效率的影响较小，类别2中的节点被破坏则对网络效率的影响较大，对最大连通子图的影响较小，而类别3中的节点被破坏时，对网络效率和最大连通子图的影响非常大，因此可以将类别3中的节点作为关键节点进行重点防护，来增强网络的抗毁性.同时，类别3中的节点与文献[4]中识别出的关键节点一致，说明了本文采用聚类算法对地铁网络的关键节点识别是有效的.

4 结 论

1) 由于聚类划分的各节点类之间存在着差异，可通过比较各节点类聚类中心的类别中心值实现关键节点的识别.

2) 对蚁群聚类算法每次迭代所得的结果进行遗传算法变异操作，能够在一定程度上提高算法的聚类效果和求解效率.

3) 通过对成都地铁网络的鲁棒性分析发现，关键节点类被攻击之后，网络性能指标急剧下降，整个地铁网络近乎瘫痪，验证了聚类算法对关键节点识别的可行性和有效性.