无支撑大跨度甲板结构纵向稳定性试验与数值分析

万 琪 潘 曼 朱 凌* 彭营豪 徐 良 王福花

(中国船舶及海洋工程设计研究院1) 上海 200011) (武汉理工大学船海与能源动力工程学院2) 武汉 430063)

0 引 言

某些民用滚装船、车辆运输船及军用登陆舰等的顶层甲板既是露天甲板又是强力甲板，甲板下为纵通的车辆舱，顶层甲板具有大跨度无支撑的特点.大跨度顶层甲板作为船体梁的上翼板，承受着较大的拉压应力，另外还要承受露天甲板载荷、车辆轮印载荷等，其纵向受压稳定性直接决定了船体梁的极限承载能力.

针对甲板结构的极限强度，各船舶规范[1-3]已给出了相应的计算公式，但对于大跨度甲板的极限强度，还没有具体的分析指南.乔迟等[4]采用有限元方法研究了板厚、扶强材尺寸和间距对大跨度加筋板架结构强度和稳定性的影响，并探讨了以结构重量最小为目标的优化设计方法.程瑞琪等[5]基于理论分析和数值仿真方法，提出了结构试验模型与实船非线性相似方法，并通过模型试验验证了该方法的可靠性.Wan等[6]基于对大跨度甲板结构纵向屈曲强度计算方法的分析和讨论，提出了大跨度甲板结构的屈曲分析和优化设计方法，并对大跨度甲板结构的横梁和纵桁进行了优化.Zhu等[7]对计算大跨度板架中多跨梁柱纵向屈曲强度的SMITH方法进行了修正，并用有限元方法验证了修正方法的合理性.Zhu等[8-9]应用“第一性原理”评估了矿石运输船舱口甲板结构的强度，并提出了极限强度的简化计算方法.同时，采用非线性有限元法对舱口甲板的极限强度进行了计算分析，并以此验证了简化计算方法的合理性.

目前，对无支撑大跨度甲板结构的极限承载力还没有进行深入的研究和探讨，开展此类甲板结构的极限承载能力研究对指导船舶结构设计具有重要意义.因此，本文开展了大跨度甲板结构的极限承载能力试验，并结合有限元方法对实尺度甲板结构和模型甲板结构的极限承载力进行了计算分析.

1 模型设计

根据实际大跨度上甲板的结构特点和与船体的连接，结合试验条件和数值分析结果，选择平行中体上甲板结构进行全尺寸简化箱梁模型设计.以此模型为基础，选取不同的长度和厚度尺度比，设计出基准剖面，基于基准剖面进行骨材合并，骨材合并时保证板格的临界应力、甲板的剖面模数和甲板的截面积满足相似变化关系，从而设计出畸变缩比试验模型.再对此缩比试验模型进行甲板稳定性试验.

1.1 实尺度简化模型设计

箱型梁模型的简化原则为：①顶层甲板结构按实际图纸进行设计；②舷侧板、纵舱壁和下甲板的设计保证在加载过程中，模拟边界条件和提供足够的刚度，使顶层甲板率先发生屈曲破坏.

设计的实尺度简化箱型梁模型(以下简称“简化模型”)结构的横剖面图剖面主要参数见图1和表1.

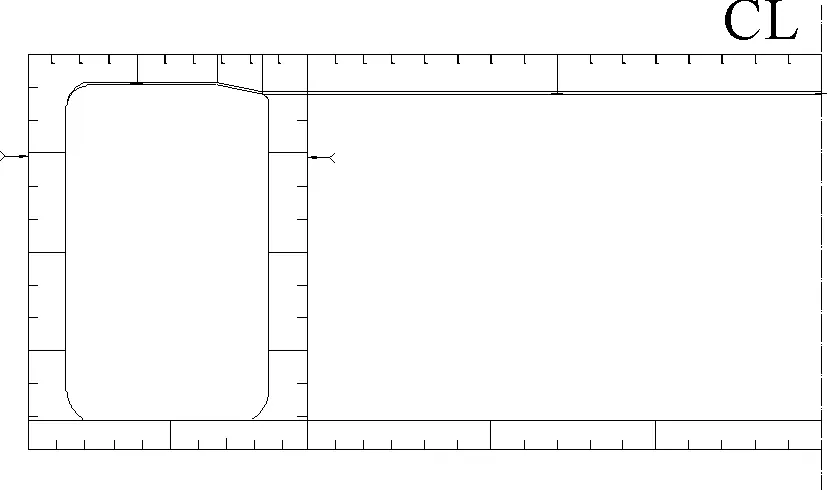
图1 简化模型横剖面图(半宽)

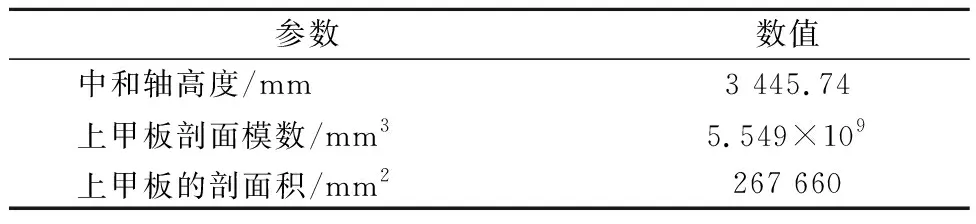
表1 简化模型剖面的主要参数

1.2 简化模型屈曲分析

非线性方程组迭代法设定为Newton-Raphson迭代方法，迭代控制用Riks弧长法.Riks弧长法可很好地控制结构的变形和载荷，让迭代分析路径沿着结构的平衡路径进行.运用大变形、有限应变和Von-Mises屈服准则，并采用载荷控制，模型的材料为屈服应力σy=355 MPa的理想弹塑性材料，弹性模量E=210 GPa，泊松比υ0.3.为了准确模拟船体甲板板筋组合失稳屈曲行为，板和强弱骨材的腹板采用壳(shell)单元，骨材面板采用梁(beam)单元，有限元计算模型见图2.模型计算时采用的边界条件见表2.

图2 简化箱型梁的有限元计算模型

表2 非线性有限元模型的约束条件

采用Riks弧长法对箱型梁在中垂条件下的极限强度进行计算，其计算结果见图3.得到该模型的极限承载能力为

Msimplified=1.928×1012N·mm

(1)

1.3 缩尺模型设计

综合各种试验条件的分析，本试验应用相似理论来指导模型设计.结合试验设备的加载能力和施工工艺限制，简化模型与缩比模型的板厚比例定为Ct=14∶3，长度的比例确定为CL=9∶1.在模型设计阶段，暂时将简化模型与缩比模型材料取为相同，及材料换算系数Cσ=1，此时，基准剖面的每项参数所对应的相似关系应满足：

(2)

(3)

CA=CLCt=126/3=42

(4)

式中：CM为弯矩换算系数；CW为剖面模数换算系数；CA为截面积换算系数.

对于小而密的纵骨，若按照实际相似变化，会使得间距过小，而难以加工，且在板中产生较大的焊接残余应力.根据模型加工的工艺条件，在2～3 mm的板上焊接骨材的适宜间距为130～180 mm，因此纵骨合并之后的间距取为150 mm.在确定骨材间距之后，进行板格临界应力的校核，可以得到在合并过程中顶层甲板的板格恰好满足临界应力相似要求.为便于加工，模型的纵骨间距按照甲板的主要部分的尺寸进行变换.

经过骨材处理，缩尺模型构件尺寸见表3，横剖面图见图4.

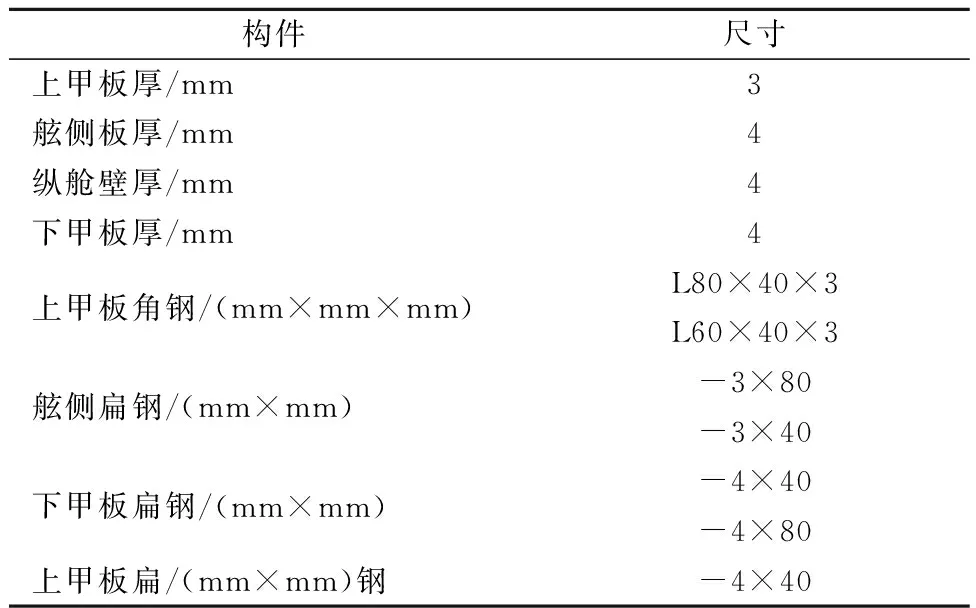
表3 骨材合并后的剖面详细构件尺寸

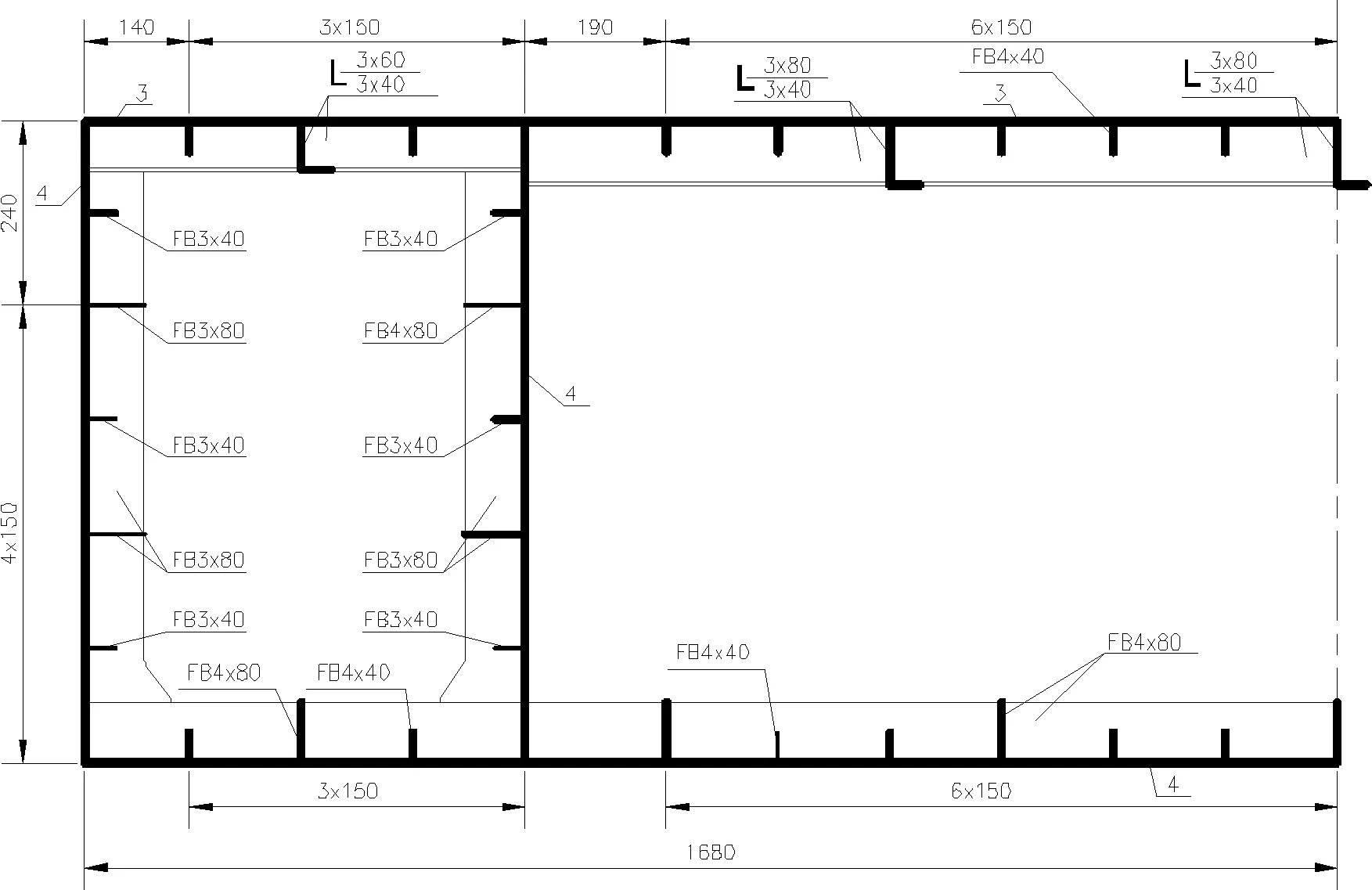
图4 缩尺模型的横剖面图

1.4 原模型和缩尺模型的相似性检验

为检验目标甲板区域与设计模型之间是否有相同的应力分布，从而验证模型设计的合理性，通过有限元计算的结果验证二者的相似性.首先在简化模型的端面施加弯矩1.215×1012N·mm，缩比模型的端面根据相似关系施加弯矩3.2×109N·mm，此时端面弯矩满足式(2)，简化模型和试验模型应有相同的应力分布，表明简化模型和试验模型在线性范围内满足相似关系.检验点分别选取甲板中心处的甲板板、纵桁和纵骨上的单元(检验点1、2、3).线性段应力对比见表4.

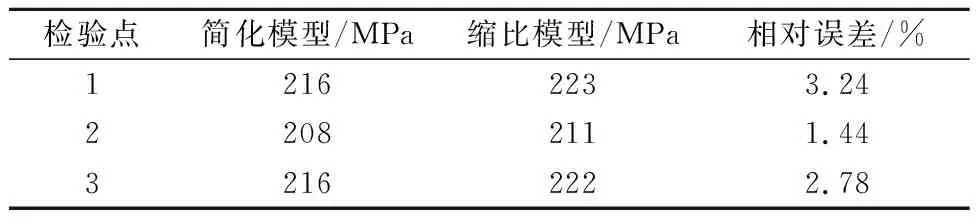
表4 简化模型和缩比模型线性段的应力对比

图5 极限状态下的应力云图

(5)

基于两个模型线性段和非线性段数值模拟结果的相似性对比可知，误差在限制范围内.以此证明，使用比例模型进行试验是可靠的.

2 试验研究

2.1 试验过程

本试验模型包括加载段和试验段，加载段和试验段在外型上保持一致，但是加载段刚度增加数倍，考虑到横舱壁的传力效果较好，所以在加载段和试验段联结处设置一个10 mm厚的横舱壁，以保证加载段的刚度足够大以达到传力和压垮试验段的效果，为了便于焊接，横舱壁向模型外侧延长50 mm，见图6.

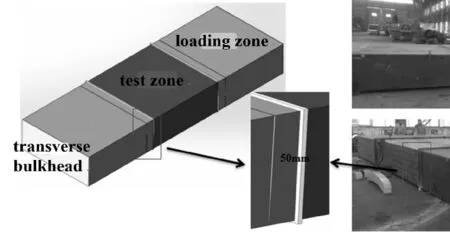
图6 试验模型图

试验的加载方式采用四点弯曲，来模拟顶层甲板受压的工况.分别在模型首尾段设置圆钢基座模拟简支约束，在距离试验段240 mm的横舱壁处加载，形成在纵向方向上的四点弯曲，图7为试验模型的加载示意图.

图7 试验模型加载示意图

模型的试验段上布置了应力测点及位移测点，其中位移的测量布置见图8.

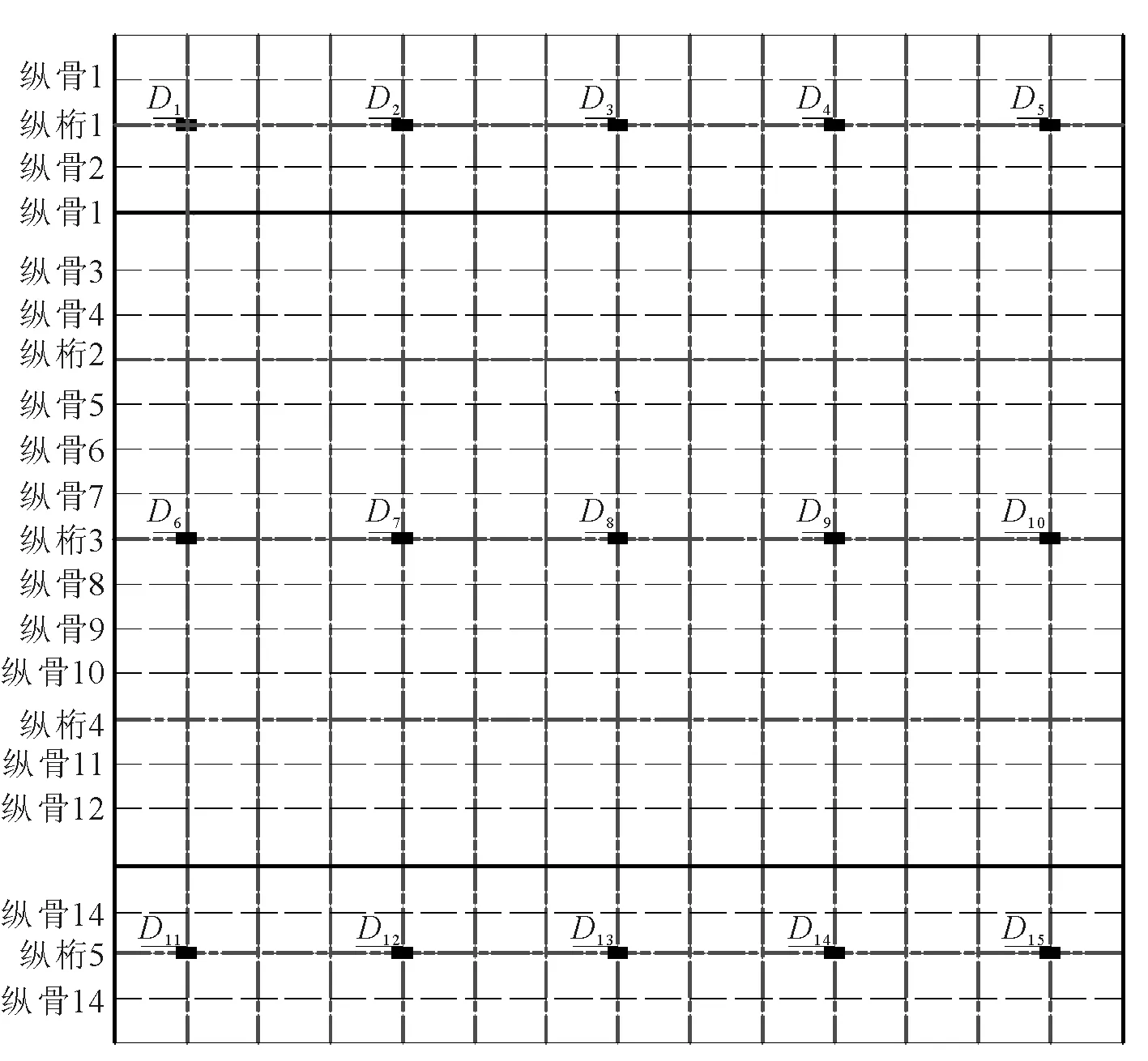
图8 位移测点示意图(俯视)

材料的性能通过拉伸试验测得，每一厚度均加工三件拉伸试件，试验模型采用钢材Q345B，经数据拟合得到试验段材料的真实应力-应变曲线见图9，并按不同厚度分别应用至有限元仿真中.

图9 材料真实应力-应变曲线

试验开始前，测量了初始变形并反复加卸载几次(模型弹性范围内)，消除加工过程中的残余应力，同时调试测试系统至完好.将测试系统和加载系统归零，试验开始：两组加载装置同时加载，每组加载装置包括1台油泵、10个千斤顶，每个千斤顶加载至100 kN之前，加载力、应变和位移每10 kN记录一次；超过100 kN但未达到150 kN时，每5 kN记录一次；之后每2.5 kN记录一次，直到载荷显示器的力显著减小时，模型破坏；最后停止加载，并缓慢卸载至零，记录应变和位移的数据，试验结束.

2.2 试验现象

试验初始阶段，油泵进行平稳加载，单个千斤顶加载力增大至202 kN后，随着载荷的继续增大，模型内发出“啪啪”的响声，结构逐步失稳；载荷增大至208 kN后，油泵已不能平稳加载，油压增加速度渐渐降低，同时模型变形速度加快，模型发出连续的响声；载荷增大至214 kN时油压已不能再继续增加，压力传感器示数迅速减小，同时变形迅速增加，模型结构开始产生塑性流动；为了让模型破坏变形更加明显，继续增加油压，但压力传感器的示数随着变形的增加而减小，减小至185 kN时，模型发出“砰”的一声巨响，出现明显的破坏波形；至此试验结束，并逐步卸载.

模型破坏时，典型部位的破坏模式见图10，上甲板的板格出现明显的凹陷和“波形”，上甲板的骨材发生柱屈曲和侧倾.加载段的两端和试验段下甲板在模型崩溃时基本无塑性变形，无破坏发生.

图10 甲板板及内部骨材的局部破坏模式

2.3 试验结果

试验过程中记录了千斤顶的载荷值P和15个位移测点的位移值D.当加载过程中载荷显示器的读数显著减小时模型发生大变形破坏，对应的载荷值为模型的极限载荷，模型破坏时，每个千斤顶的加载力约为214 kN(四点弯曲一端加载力总计P=2 140 kN，两端加载力对称)，此时各个测点对应的位移值为40 mm左右.图11为D8位移测点(试验段甲板中心点)在加载-卸载过程中的载荷-位移曲线.

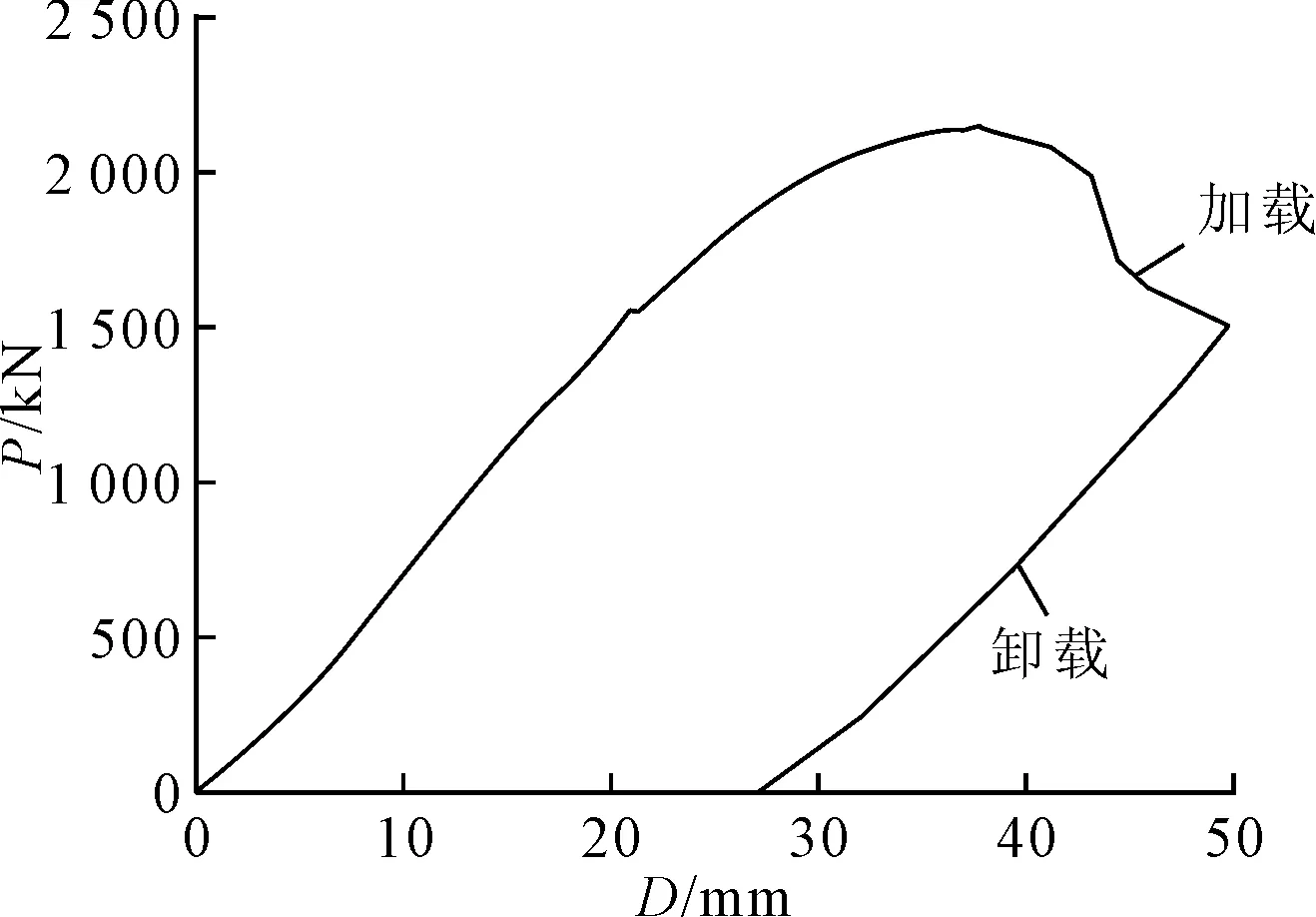
图11 位移测点D8的载荷-位移(P-D)曲线

本试验采用四点弯曲的方式保证模型在试验段受到纯弯曲，其加载形式和力矩M沿模型长度L方向的分布见图12.试验段端部的弯矩M为

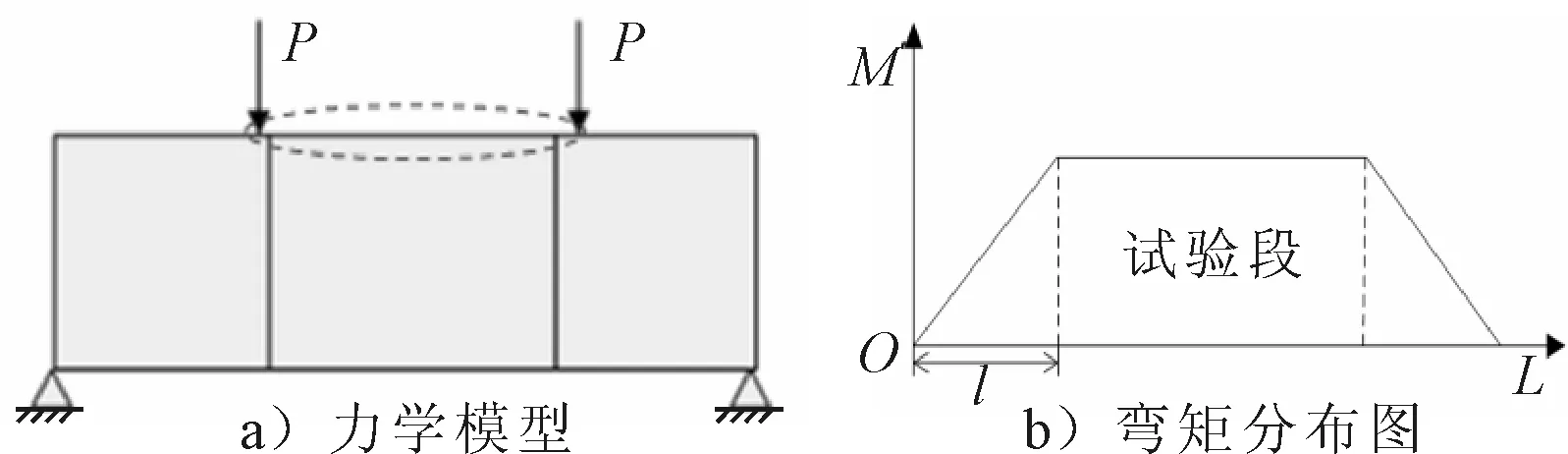
图12 四点弯曲的力学模型和弯矩分布图

M=P·l

(6)

式中：P为四点弯曲模型的一端加载力；l为加载力臂的长度.

结合结构力学知识，得到顶层甲板的平均应力：

σ=M/W

(7)

式中：M为试验段的弯矩；W为上甲板的剖面模数，试验得到顶层甲板的极限平均应力σexperi=349.95 MPa.

从载荷-位移曲线和试验现象中可以看出，加载力在1 400 kN以下时，测点的位移与外载荷之间基本呈线性关系，加载力超过1 600 kN后，试验段甲板局部区域进入塑性状态，加载至210 kN后，试验段上甲板基本进入塑性状态，模型发生崩溃.最后，得到试验模型的极限承载能力为

Mexperi=4.887×109N·mm (4.87 MN·m)

(8)

3 非线性有限元分析

3.1 试验模型有限元分析

在有限元模拟中，在模型两端设置简支约束，在第二道横舱壁上施加均布压力，均布压力的范围在模型长度方向为300 mm，模型宽度方向为3 360 mm，模拟千斤顶对模型施加的压力，加载示意图见图13.图14为试验模型有限元计算结果.

图13 有限元加载示意图

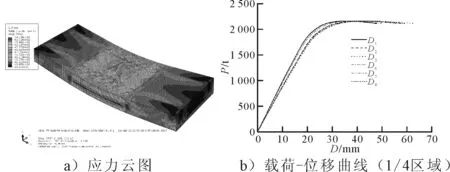
图14 试验模型有限元计算结果

试验模型有限元计算得到的极限承载能力为

MexperiFEM=4.96×109N·mm (4.96 MN·m)

(9)

3.2 试验和有限元结果对比

试验模型的非线性有限元分析考虑了实际的工装设计、测得的模型初始变形以及材料的真实特性，完全模拟试验的真实过程.将采集到的试验结果同非线性有限元计算结果进行对比，见图15.

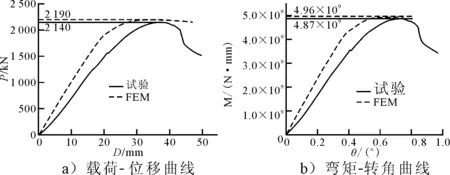
图15 试验数据与FEM结果对比

表5 试验数据与FEM结果对比

试验与非线性有限元计算的极限承载能力相对误差仅为1.85%.由于基座与圆钢之间存在摩擦力，而有限元计算时处理为理想简支边界条件，不能完全有效模拟试验的边界条件，导致试验和有限元在同一载荷水平下的位移值有差异.因此，基本可认为本有限元方法得到的模型极限承载能力的结果可靠.

4 结 束 语

为进行本次试验，项目组对于试验方案进行了长时间的反复分析、计算与调整，最终得以确定.并在试验开始之前，多次在弹性范围内采取预加载试验，加载装置，应变、变形数据采集系统均能正常工作，预实验中实验值与计算值结果吻合较为良好，满足试验条件.从测点布置、加载装置的布置和仪器设备的检查与调试，到初步加载，直至最后完成试验，整个流程与方案基本一致.试验完成后，除个别点数据采集存在异常，试验数据符合预期结果.

将采集到的试验数据同非线性有限元计算结果对比，结果吻合良好，验证了非线性有限元方法的可靠性，同时表明了试验方案的可行性，可为同类箱型梁结构和大跨度甲板结构的极限强度研究提供参考.