基于NEMA编号和合流相位的跳相序感应控制策略

张帅鹏 柳祖鹏 何雅琴 姚昌宇

(武汉科技大学汽车与交通工程学院 武汉 430065)

0 引 言

感应控制是解决城市道路交叉口交通拥堵的有效方法之一.2003年，美国电气制造商协会(national electrical manufacturers association，NEMA)面向典型的十字形信号控制交叉口，建立了具有8个机动车相位和4个行人相位，采用半环分析方法，定义起始相位和末尾相位两种机动车相位属性，讨论可能存在的相位组合方案和相位切换方案，分析相位切换过程基本规律的NEMA双环相位结构[1].

国内外学者基于NEMA双环相位结构做了一系列的研究.黄谦[2]以NEMA相位为基础，提出了一种通过排队长度算法来确定周期和绿灯时间的交通配时优化模型.乔建明等[3]发现采用基于双环8相位的交通信号控制方法,既避免相位冲突，又易形成搭接相位，操作起来标准且简单.季策[4]通过引入了NEMA双环相位结构，采用动态规划方法实现相序的灵活优化，提出了一种单交叉口实时信号控制算法.曹政等[5]以NEMA双环结构为基础制定优先度规则,以此确定动态相位组合及相序排列.

国内外学者对交叉口感应控制的相关研究，有考虑各方向车流量的[6-7]，有考虑各相位排队长度的[8-9]，有考虑车辆排队长度和排队时间的[10].韩平超[11]提出了相位需求度的概念，设计了相位需求度的计算方法和控制流程，但是相位需求度计算时只考虑了时间因素，无法合理地反映各个相位对绿灯信号的需求程度.柳祖鹏等[12]提出了绿灯需求度的概念，设计了绿灯需求度的计算方法和控制流程，但该控制流程是以相位结构固定为前提的，不能实现动态的相位组合.

对于合流相位的相关研究较少，郭英明等[13]利用VISSIM软件对不同周期不同流量条件下的交叉口合流放行状态进行仿真,结果表明：当出口车道数目与同时放行的左转和直行车道数目之和相同或大于时,合流放行相位在理论上具备一定的可行性.肖文彬等[14]提出了合流流线相容的概念并用于交叉口信号控制的相关研究.

针对NEMA双环相位结构的一些限制，例如北进口道的直行流量大，左转流量小，但南进口道的直行流量小，左转流量大，这时NEMA相位结构就无法实现调节.文中引用绿灯需求度的概念和计算方法，提出一种基于NEME编号和合流相位的跳相序感应控制策略，实现相位的动态组合，以解决城市道路交叉口交通拥堵问题.

1 NEMA双环相位车流编号及其规律

NEMA双环相位结构由8股机动车相位组成，见图1.车流1、3、5、7为左转车流，车流2、4、6、8为直右车流，NEMA双环相位结构见图2.同时，在将编号为9、10、11、12、13的虚拟车流分别对应编号为1、2、3、4、5的实际车流后，可以发现规律：设置编号为i的车流，当i为奇数时，与编号为i+3，i+4，i+5的车流分别构成合流、交叉、分流三种相位效果组合；反之，当i为偶数时，与编号为i+3，i+4，i+5的车流分别构成分流、交叉、合流三种相位效果组合.如编号为4的车流，4为偶数，与编号为7(4+3)的车流为分流，与编号为8(4+4)的车流为交叉，与编号为1(4+5)的车流为合流，见表1.

图1 NEMA机动车相位编号图

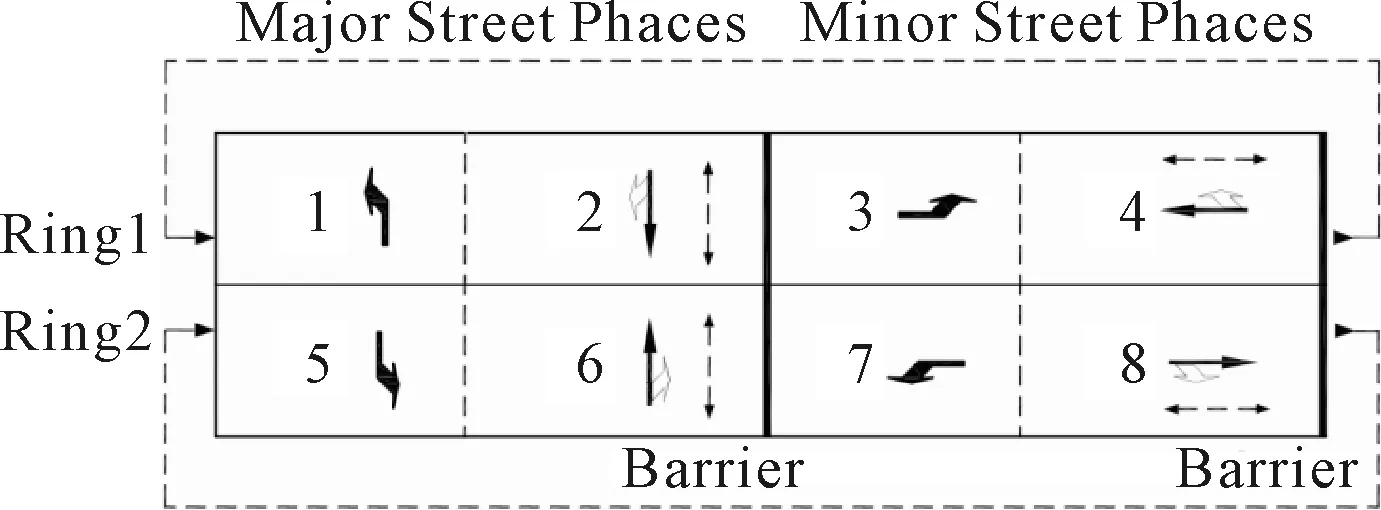
图2 NEMA双环相位结构图

表1 NEMA机动车相位组合规律表

在考虑合流的前提下，8股车流的全部组合见表2.在考虑合流的前提下，8股车流的全部组合共有3×4=12种，其中(1,4)，(3,6)，(5,8)，(7,2)为合流.

2 合流相位

合流相位是指在同一出口道汇合的左转和直行车流同时放行的绿灯相位.基于已有研究表明：当出口车道数目与同时放行的左转和直行车道数目之和相同或大于时,合流放行相位在理论上具备一定的可行性.在本研究中，交叉口背景符合车道平衡条件，车辆在在交叉口内左转或直行时严格按照规定车道行驶且不会变道.根据NEMA相位的车流编号，合流相位有四种情况：(1，4)，(3，6)，(5，8)，(7，2)为合流相位.以合流相位(1，4)为例，示意图见图3.

图3 (1，4)合流相位示意图

3 绿灯需求度

绿灯需求度(demand degree of green, DDG)是指不同相位在周期中的不同时间对绿灯信号的需求程度.处于红灯相位下的车流的绿灯需求度与等待时间和排队车辆数有关.为了统计红灯相位下的排队车辆数，在紧靠停车线的下游(停车线与人行横道之间)布设“检出检测器”，在进口道上游大于最大排队长度的位置布置“检入检测器”，不间断统计检入、检出检测器上的车辆到达脉冲，检入脉冲时排队数增加，检出脉冲时排队数减少，由此可统计得到各个相位在不同时刻的排队车辆数.检测器位置见图4.

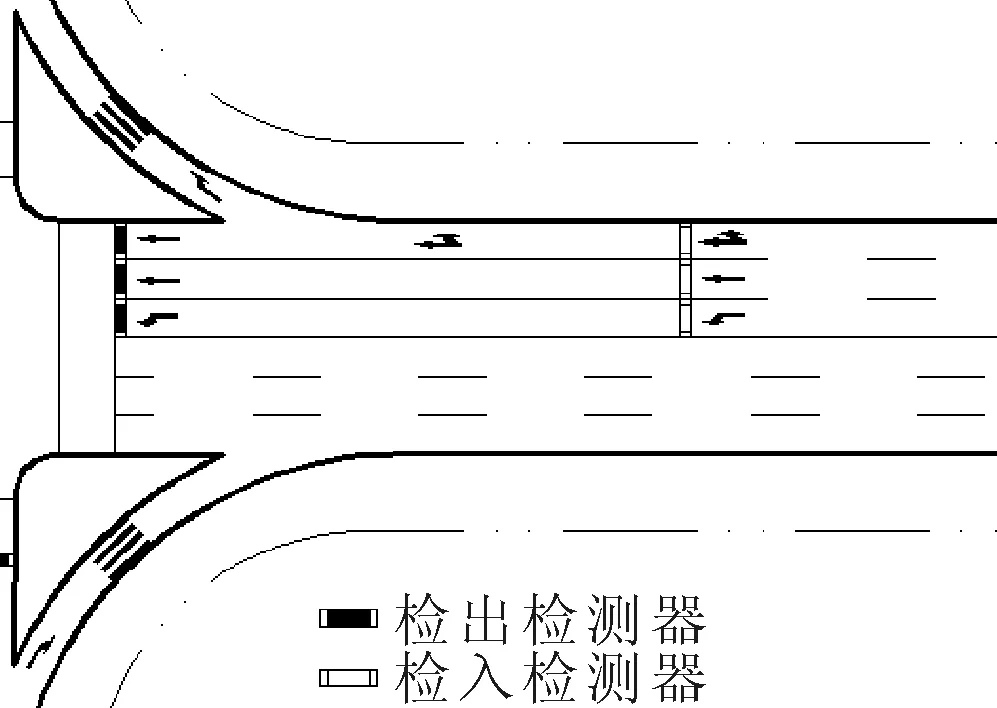
图4 检测器位置示意图

红灯开始时，累加该相位下每1s时间内的等待车辆数，即累加该相位下每一辆车已经等待的时间，计算公式为

(1)

式中：DDG为绿灯需求度，veh·s；R为当前红灯时间；t为时间变量，从1增加到R；veh(t)为t-1～t这1 s内该相位下的排队车辆数.

根据车辆检测器的检测信息，经统计可以得到该相位下每1 s的车辆排队数veh(t)，由此计算得到的绿灯需求度可以全面的反映红灯相位下的等待时间和排队情况.从而使得排队车辆较多且等待时间较长的车流所在的相位获得优先通行权.

4 感应控制策略

4.1 相位切换

相位切换分为三种情况，以相位最小绿灯时间和相位最大绿灯时间为分界点，表示为：

1) 任一相位绿灯起始，在感应信号控制内设置最小绿灯时间，在最小绿灯时间结束之前，不进行相位切换.

2) 到最小绿灯时间结束时，如果在一个预先设置的时间间隔内没有后续车辆到达，切换相位；如果有车辆到达，则延长绿灯时间，只要不断有车到达，绿灯时间可继续延长，直到预设的最长绿灯时间.

3) 当相位绿灯时间大于等于最大绿灯时间时，切换相位.

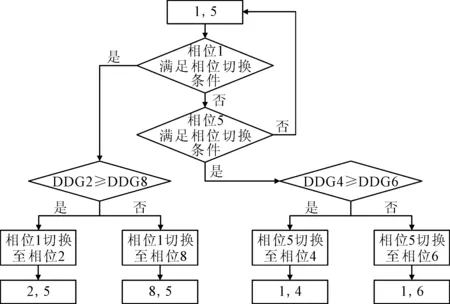
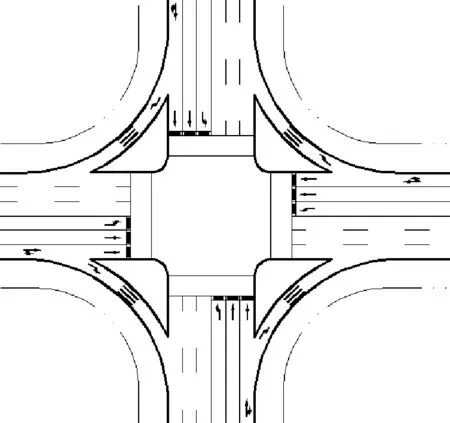
用数学表达式表示为以下三个阶段：①0≤t相

4.2 相位选择

采用全感应控制，以NEMA双环结构中定义的8个机动车相位为基础，在8个机动车相位对应进口道上都设置检测器，并根据车辆检测器的检测信息，计算得到对应相位的绿灯需求度.在每一次选择下一个切换相位时，选择此时不冲突且绿灯需求度最大的相位为下一个变换相位.

通过相关研究和观察可知，在NEMA相位结构中，交叉口至多只能使2股机动车相位的车流同时通过，通常情况下，为了使交叉口时空资源得到充分利用，交叉口信号控制都是以2股机动车相位为基础，这样既充分利用了资源，又避免了冲突.处于绿灯状态下的2股机动车相位，当其中1股机动车相位满足相位切换条件时，选择该机动车相位对应的不冲突且绿灯需求度最大max(DDGi)的相位进行切换.以相位1和5为例，示意流程图见图5.

图5 相位切换示意流程图

5 仿真测试与分析

5.1 仿真测试环境

以武汉市团结大道-园林路交叉口为例，该交叉口4个进口道均为3车道，其中直行与右转共用2车道，左转专用1车道.见图6.

图6 交叉口布局示意图

仿真运行时，共运行4 000 s，前400 s作为路网车流初始化阶段.设置多个仿真种子运行仿真试验，试验结束后输出所有车辆的平均延误作为评价指标.

5.2 仿真场景

根据车流流量差异设置“流量均衡”“流量不均衡”和“特殊流量”三种场景.①流量均衡场景下，主、次干路流量比约为3∶2，左、直、右流量之比为3∶6∶1，上下两环的流量之和基本相等，车流1+车流2约等于车流5+车流6，车流3+4约等于车流7+8.②流量不均衡场景下，主、次干路流量比约为3∶2，上环流量之和大于下环流量之和，车流1+2大于车流5+6，车流3+4大于车流7+8.③特殊流量场景下，主、次干路流量比约为3∶2，上下环流量之和基本相等，车流1+2大于车流5+6，车流7+8大于车流3+4.以上3种场景下，再分别设置低、中、高三种不同的饱和度，交叉口的流量分别为2 000，4 000和5 600辆/h.

设置两种感应控制方案：①NEMA双环结构感应控制，用“NEMA”表示；②基于绿灯需求度的跳相序感应控制，用“DDG+M”表示.

5.3 仿真结果及分析

汇总多次仿真实验的平均延误评价数据，得到3×3=9种不同条件下的交叉口平均延误对比图，见图7.

图7 不同场景下，不同饱和度的延误对比

由图7可知，流量均衡场景下，相较于NEMA控制策略，DDG+M控制策略的延误整体较大，其中在高饱和度情况下，相较于NEMA控制策略，DDG+M控制策略下的平均延误增加了2.26 s，增加了4.5%.流量不均衡场景下，相较于NEMA控制策略，DDG+M控制策略的延误整体较小，其中在高饱和度情况下，相较于NEMA控制策略，DDG+M控制策略下的平均延误减少了4.02 s，降低了5.5%.特殊流量场景下，相较于NEMA控制策略，DDG+M控制策略的延误整体较小，其中在高饱和度情况下，相较于NEMA控制策略，DDG+M控制策略下的平均延误减少了17.68 s，降低了22.4%.由此可见，相较于NEMA控制策略，DDG+M控制策略更适用于流量不均衡和特殊流量场景的交叉口.

不同饱和度条件下，不同场景的延误对比图，见图8.

图8 不同饱和度条件下，不同场景的延误对比

由图8可知，低饱和度条件下，三种场景下的两种控制策略的延误相差不多，原因是交通流量过小，各车流在最小绿灯时间内均完全驶入交叉口，无法凸显控制策略调节效果.中饱和度条件下，三种场景下的两种控制策略的延误相差不多，都在1 s以内，原因是交通流量适中，两种控制策略的调节效果差距不明显.高饱和度条件下，两种控制策略调节效果开始凸显，在高饱和度流量均衡场景下，相较于NEMA控制策略，DDG+M控制策略下的平均延误增加了2.26 s，增加了4.5%.在高饱和度流量不均衡场景下，相较于NEMA控制策略，DDG+M控制策略下的平均延误减少了4.02 s，降低了5.5%；在高饱和度特殊流量场景下，相较于NEMA控制策略，DDG+M控制策略下的平均延误减少了17.68 s，降低了22.4%.

汇总不同流量场景和不同饱和度条件下，NEMA和DDG+M控制策略的延误对比，见图9.由图9可知，在流量均衡场景下，NEMA控制策略较优，但两者交叉口平均延误相差不大；在流量不均衡和特殊流量下，DDG+M控制策略较优，特别是在流量不均衡和特殊流量场景的高饱和度交叉口，DDG+M控制策略都具有明显的优势.

图9 各种组成场景下的延误对比

6 结 束 语

基于NEMA双环相位结构的相关研究，充分证明了NEMA相位的合理性和在交叉口控制中的优势，其对于相位的定义以及独有的具有规律的相位编号方式方便了相关研究.红灯相位下的绿灯需求度的计算方法充分考虑了车辆的排队和等待时间，合理地反映出了各个红灯相位对于绿灯信号的需求程度.在满足当出口车道数目与同时放行的左转和直行车道数目之和相同或大于时的前提下，合流相位的存在将实现交叉口相位的动态组合.

仿真测试和结果表明，在流量不均衡和特殊流量的交叉口，基于绿灯需求度的感应控制策略比NEMA双环相位结构更有效，且其控制效果随着流量的增加表现得越来越明显.

后续拟在车辆以车队行驶方式到达的条件下，进一步对该控制策略进行验证和改进.单点信号控制是干线协调控制的基础，后续研究可在单点控制的基础上扩展到干线甚至区域层面，并在实践中进行测试和验证.