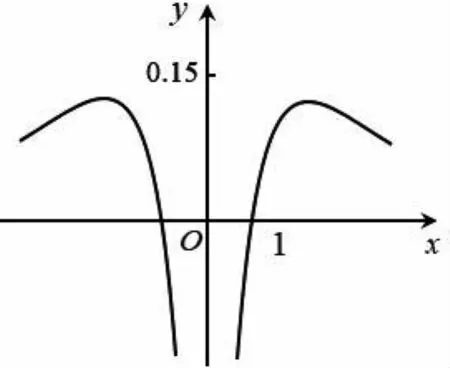
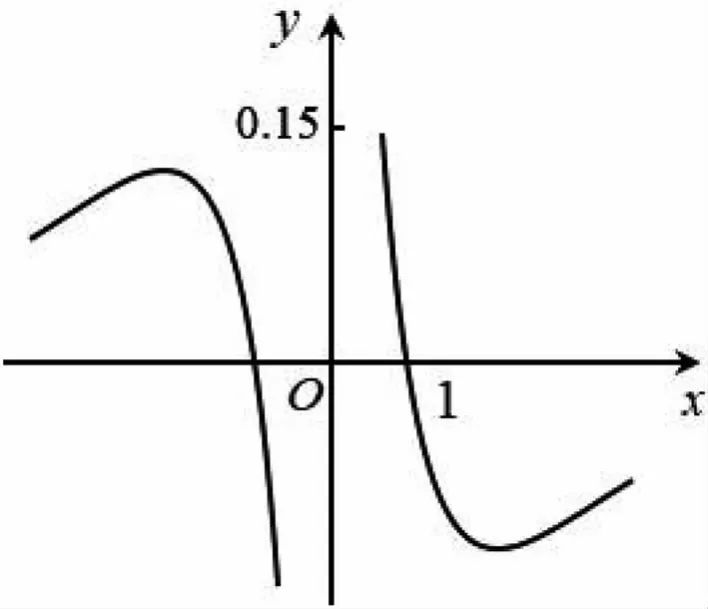
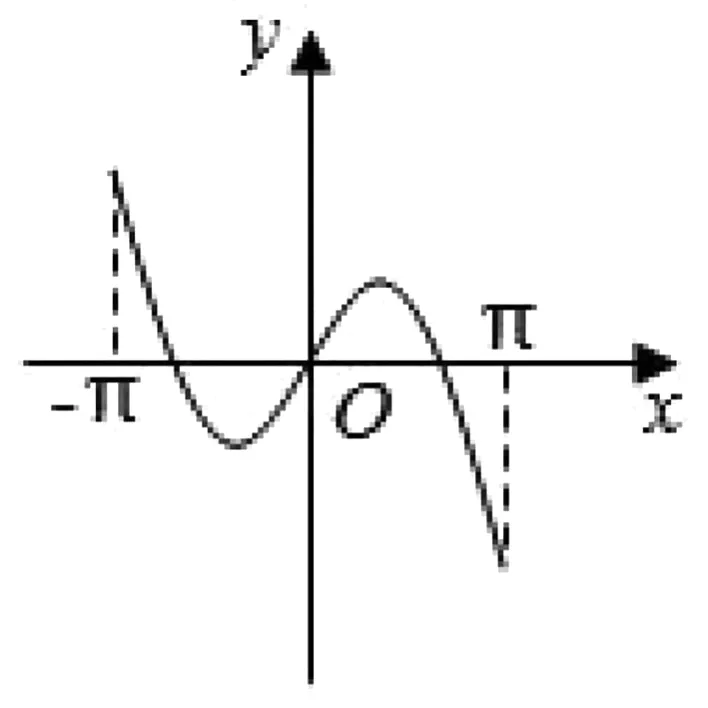
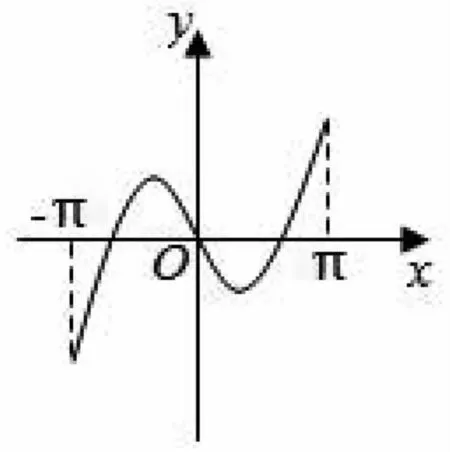
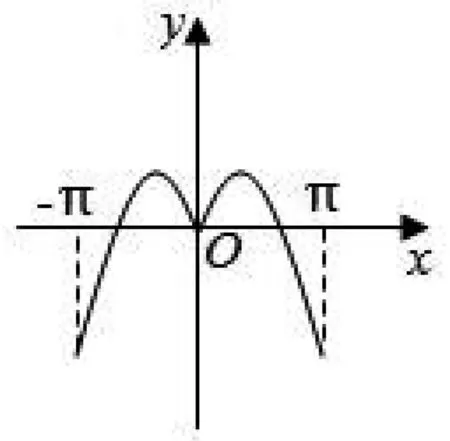
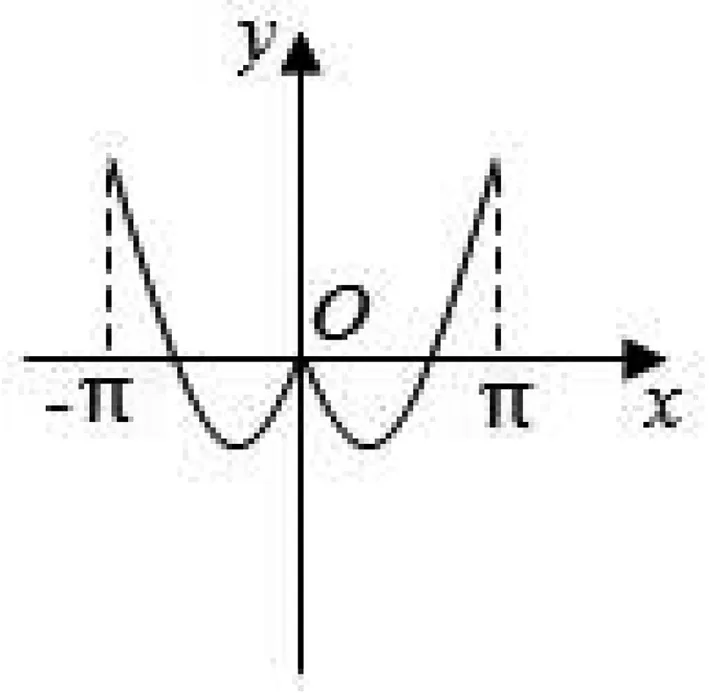
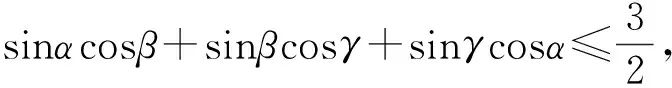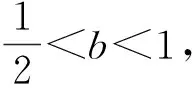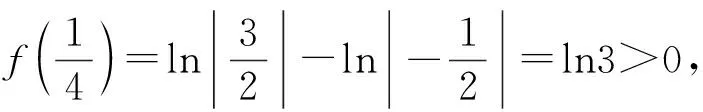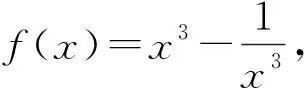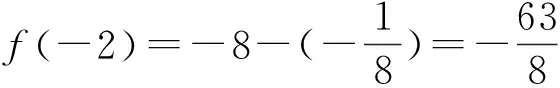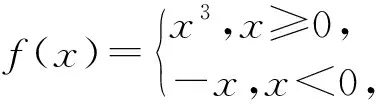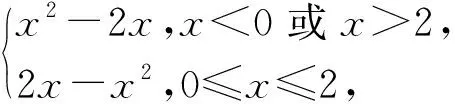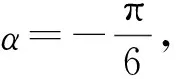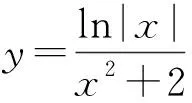妙用特殊值 巧解高考题

北京市第一0一中学怀柔分校 (101407) 李加军

山东省栖霞市观里中学 (265314) 徐艳华

近两年各地高考数学试题各有千秋，从不同角度考查了学生数学的“四基”、“三会”和六大数学核心素养，给人以赏心悦目的感受.纵观各套试卷，如果抓住一般与特殊的关系，灵活寻求特值，充分发挥数学运算核心素养，有些试题可以迎刃而解，达到以四两拨千斤的效果.

例1 (2020年北京)已知函数f(x)=2x-x-1，则不等式f(x)>0的解集是( ).

A.(-1,1) B.(-∞,-1)∪(1,+∞)

C.(0,1) D.(-∞,0)∪(1,+∞)

分析：本题旨在借助函数y=2x和y=x+1的图象，观察图象可得结果，对有些同学会有点难度.但是观察选择项，只需验证特殊值即可.

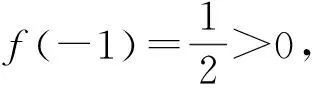
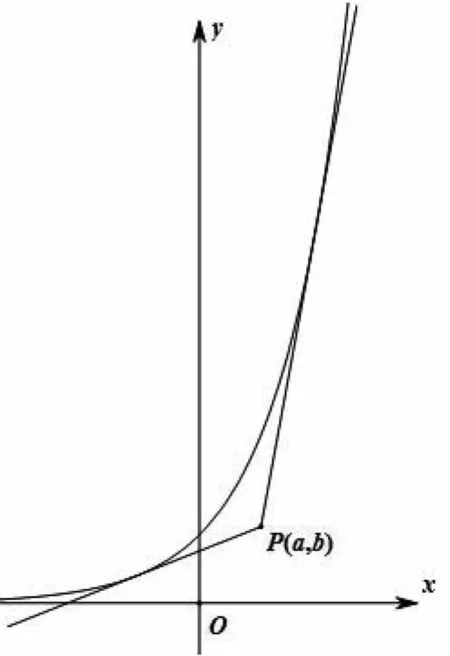
例2 (2021年全国新高考)若过点(a,b)可以作曲线y=ex的两条切线，则( ).

A.eb

分析：结合曲线y=ex的图象直观即可判定点(a,b)在曲线下方和x轴上方时才可以作出两条切线，再结合选项列举两组特值排除a,b所不满足的关系，由此确定正确选项.

解：画出函数y=ex的图象，如图1所示，根据直观即可判定点(a,b)在曲线下方和x轴上方时才可以作出两条切线.

图1

A.abC.aba2

分析：先考虑函数的零点情况，注意零点左右附近函数值是否变号，结合极大值点的性质，选取两组特值进行验证，排除a,b所不满足的关系，由此确定正确选项.

A.0 B.1 C.2 D.3

例5 (2020年山东)若定义在R的奇函数f(x)在(-∞,0)单调递减，且f(2)=0，则满足xf(x-1)≥0的x的取值范围是( ).

A.[-1,1]∪[3,+∞) B.[-3,-1]∪[0,1]

C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3]

分析：此题首先根据函数奇偶性与单调性，得到函数f(x)在相应区间上的符号，再根据两个数的乘积大于等于零，分类转化为对应自变量不等式，最后求并集得结果.但这一过程很多同学可能会不太清晰，如果借助特值，结果马上水落石出.

解：记g(x)=xf(x-1)，且xf(x-1)≥0即g(x)≥0的解集为M，首先因为g(2)=2f(1)=-2f(-1)>-2f(-2)=2f(2)=0，所以2∈M，排除A，B，其次g(4)=4f(3)=-4f(-3)<-4f(-2)=4f(2)=0，所以4∉M，排除C，故选D.

例6 (2020年新课标Ⅰ)若2a+log2a=4b+2log4b，则( ).

A.a>2bB.a<2bC.a>b2D.a

分析：本题主要考查函数与方程的综合应用，涉及到构造函数，利用函数的单调性比较大小，对学生有些难度.如果适当选取几个特值进行验证，可以顺利解决此题.

例7 (2020年全国Ⅱ理)设函数f(x)=ln|2x+1|-ln|2x-1|，则f(x)( ).

分析：本题考查函数的奇偶性以及复合函数的单调性，如果学生的运算化简能力稍弱，可能会出现错误判断.借助特值运算，可以降低试题的难度，轻松过关.

A.是奇函数，且在(0，+∞)单调递增

B.是奇函数，且在(0，+∞)单调递减

C.是偶函数，且在(0，+∞)单调递增

D.是偶函数，且在(0，+∞)单调递减

分析：本题考查函数的奇偶性以及单调性，难度不大，但借助特值判断，可以提高准确率.

例9 (2020年新课标Ⅱ)若2x-2y<3-x-3-y，则( ).

A.ln(y-x+1)>0 B.ln(y-x+1)<0

C.ln|x-y|>0 D.ln|x-y|<0

分析：本题考查对数式的大小的判断问题，解题关键是将不等式变为2x-3-x<2y-3-y，通过构造函数f(t)=2t-3-t的方式，利用函数的单调性得到x,y的大小关系，考查了转化与化归的数学思想，但对许多同学来说并不简单.如果通过验证特值或许就顺手得到结果.

解：易知取x=1，y=2符合条件，此时排除B, C, D,故选A.

解：取k=1，则h(x)=|x2-2x|=

例11 (2020新课标Ⅱ理)若α为第四象限角，则( ).

A.cos2α>0 B.cos2α<0 C.sin2α>0 D.sin2α<0

分析：由α为第四象限角推出2α的范围，然后判断2α的正、余弦值的正负.选两个特值可以快速得出结论.

例12 (2020年新课标Ⅰ文)已知集合A={x|x2-3x-4<0},B={-4,1,3,5}，则A∩B=( ).

A.{-4,1} B.{1,5} C.{3,5} D.{1,3}

分析：首先解一元二次不等式求得集合A，之后利用交集中元素的特征求得A∩B，得到结果.试题虽然简单，但结合选择项，选特值计算更快更准.

解：设f(x)=x2-3x-4，易验证f(1)=-6<0及f(3)=-4<0得1∈A∩B且3∈A∩B，故选D.

A

B

C

D

分析：先判断函数的奇偶性，再判断函数值的特点.因此直接取几个特殊值即可.

例4 (2020年浙江)函数y=xcosx+sinx在区间[﹣π，π]上的图象可能是( ).

A

B

C

D

分析：先判断函数的奇偶性，再判断函数值的特点.因此直接取几个特殊值即可.

解：令y=f(x)=xcosx+sinx，f(π)=πcosπ+sinπ=-π<0，且f(-π)=-πcos(-π)+sin(-π)=π，排除B，C，D，故选A.

高考试题的解答固然需要扎实的基本知识，但辅之以灵活的方法将使我们如虎添翼，更加简便快捷地解决一些问题.