一道四点共圆问题的多解及其命题背景探究

南京师范大学附属扬子中学 (210048) 郝结红

江苏省南京市溧水区教育局教研室 (211200) 魏国兵

1 模考试题呈现

(南京市2021届高三年级第二次模拟考试第21题)已知直线l：y=x+m交抛物线C：y2=4x于A，B两点.(1)略；(2)如图1，若点M，N在抛物线C上，且关于直线l对称，求证：A，B，M，N四点共圆.

图1

2 学生解法汇总

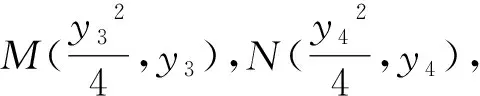
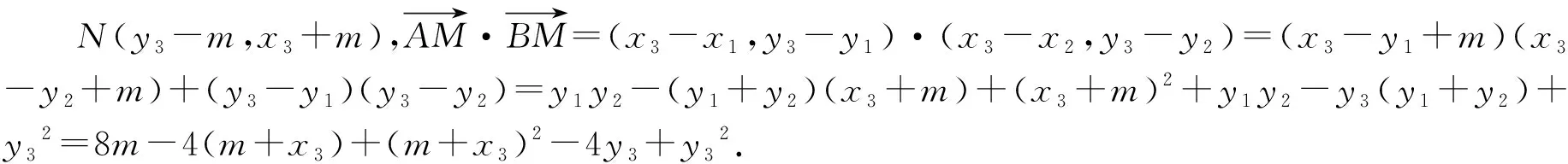
评析：以上4种解法本质是相同的：一是将四点共圆这个几何问题，转化为向量数量积为0这个代数问题；二是都是通过设坐标，利用斜率关系和中点关系，将题目条件进行坐标转化和坐标消元.所以说：在解析几何中，几何指挥代数，代数为几何服务，化归坐标永远是王道.

评析：利用与圆心和半径解决四点共圆问题，也是一种好思路，用m表示半径，用n表示半径，还需要寻找两者的关系n+m=-4进行消元.

解法6：(曲线系方程法)因为点M,N在抛物线C上，且关于直线l对称，所以可设直线MN：x+y+n=0，由A，B，M，N满足方程x-y+mx+y+n+2y2-4x=0，即x2+y2+(m+n-8)x+(m-n)y+mn=0，所以A，B，M，N四点共圆.

评析：具有某种共同性质的所有曲线的集合，称为一个曲线系，并用含有参数的方程表示.此解法中，过两直线L1：A1x+B1y+C1=0，L2：A2x+B2y+C2=0与二次曲线F(x，y)=0交点的曲线系方程为λL1L2+μF(x，y)=0.巧妙利用曲线系方程，大大降低了运算难度.

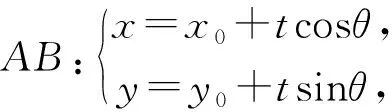
评析：巧妙利用直线的参数方程，也降低了运算难度.

3 命题背景探究

探究1 改变原题中抛物线方程，四点共圆仍然成立.

探究2 改变原题中直线l的斜率，四点共圆不成立.

探究3 将原题中抛物线方程改为椭圆方程，四点共圆仍然成立.

(1)证明：点P在C上；(2)设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上.

评析：此题揭示两条斜率之和为0的直线与椭圆相交所得的四点共圆.

简解：(1)易得C的方程为y2=4x；

评析：此题揭示抛物线上四点共圆是有条件的.

圆锥曲线四点共圆定理若两条直线y=kix+bi(i=1，2)与圆锥曲线ax2+by2+cx+dy+e=0(a≠b)有四个交点，则四个交点共圆的充要条件是k1+k2=0.

证明：两直线组成的曲线方程为(k1x-y+b1)·(k2x-y+b2)=0，则过四个交点的曲线方程可设为(k1x-y+b1)(k2x-y+b2)+λ(ax2+by2+cx+dy+e)=0①.

(必要性)若四点共圆，则方程①表示圆，那么①式左边展开式中xy项的系数为零，即有k1+k2=0.

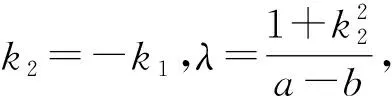
方程②的几何意义是如下三种情形之一：表示一个圆、表示一个点、无轨迹.由题设知四个交点在方程②所表示的曲线上，故方程②表示圆.

评析：上述定理用文字表述，即斜率均存在的两条直线与圆锥曲线(圆除外)有四个交点，则四个交点共圆的充分条件是两直线的斜率互为相反数.这是一个非常简洁的充要条件，运用这个定理可解决圆锥曲线上四点共圆的高考难题和数学问题.