基于教材习题的深度教学实践与反思

广东省佛山市顺德区容山中学 (528303) 潘敬贞

广东省东莞市麻涌中学 (523000) 骆妃景

1 引言

众所周知，教材是课程标准的载体，是教材编写者的集体智慧，也是师生教学的主要材料.从历年高考试卷分析看，很多高考试题都是从教材习题改编、综合、延伸、拓展、嫁接而来，具体表现为教材习题的数据的变更，条件的拓展，背景的变换以及结论的应用.因此，在平时的教学和高三复习过程中，一定要重视教材，尤其要重视对教材中经典题目的深入研究，本文对教材一道习题进行分析、变式探究以及类比拓展来激活教材习题，试图构建深度教学与同行交流.

2 案例描述

2.1 片段一：问题呈现，挖掘设问

问题(人教版选修2-1第73页习题6)直线y=x-2与抛物线y2=2x相交于A，B两点，求证：OA⊥OB.

师：同学们，大家来看一下这个问题.(过了片刻)

师：哪位同学来说一下自己的想法？(在老师的引导下让学生有充分表达自己想法的机会)

生1：我想将问题转化为直线斜率进行证明，即证明kOA·kOB=-1.

师：非常好！这位同学是从直线斜率角度对该问题进行证明，其他同学还有不同的想法吗？

师：非常好！这位同学是想利用向量工具进行求证，平面向量是解决平面解析几何的重要工具.

师：这两位同学都是想将几何问题转化为代数，利用代数方法解决几何问题，其中关键问题是什么？

生3：最关键是坐标化，即联立直线方程与抛物线方程求交点坐标.

师：大家动手试试.(大概过了2-3分钟)

师：哪位同学展示一下.

师：还有其它解法吗？

师：如果联立直线与曲线方程消元后得到的一元二次方程容易求解的，求两点的坐标也不失为好选择，关键在于选择合适方法，优化运算，简化解题过程，提高解题效率.

师：请大家思考，根据已有的解题经验，本题中的“OA⊥OB”还可以怎么处理？

此时给足学生回忆与联想，最终师生共同归纳出：

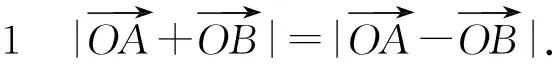
变形2 以AB为直径的圆经过坐标原点O.

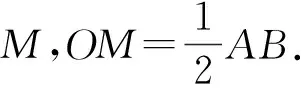
变形4 设A，B的中点为M，且OM⊥AB，OM2=AM·BM.

设计意图:高三后阶段复习中，回归教材，设计低起点的课本习题，旨在激励更多的学生参与课堂活动，实现一题多解；问题变形处理环节意在联系平面几何知识沟通平面向量工具，构建知识体系，拓展学生的思维，提高学生转化与化归能力.

2.2 片段二：问题驱动，一题多变

变式1 若直线y=3(x-2)与抛物线y2=2x相交于A，B两点，试问：OA⊥OB？

师：大家动手试一下.(过了几分钟)

师：哪位同学来展示一下.

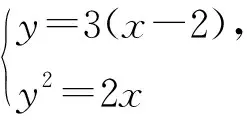
师：这位同学做的非常漂亮，主要用向量工具和韦达定理，思路清晰，过程简洁，大家掌声鼓励！(此时教室响起了热烈的掌声！)

变式2 若直线AB过点(2,0)且与抛物线y2=2x相交于A，B两点，试问：OA⊥OB？

师：大家动手试试这道题.(几分钟后)

师：哪位同学来展示一下.

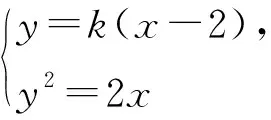
师：非常棒，这位同学思维严谨，他在设直线的点斜式方程时很细心，先考虑直线斜率不存在的情况，这是很多同学容易遗漏的.

设计意图：改变源问题的条件，由特殊到一般进行变式探究，一方面巩固源问题中涉及到的数学方法，培养学生大胆猜想，小心求证的数学品质，另一方面，也为得到一般结论做铺垫.

教师通过投影展示不同学生的解答情况，并对学生解答中存在的“亮点”和“不足”作出必要的点评.

师：本题求解过程中存在几点不足：一是有学生在设直线方程时用点斜式方程，遗漏了直线斜率不存在的情形；二是y1y2是通过k(x1-2)(x2-2)=kx1x2-2k(x1+x2)+4k增加了计算量.

师：大家反思总结以上几道试题，大胆猜想有没有什么发现.

生7：直线过定点(2,0)时，满足OA⊥OB.

师：非常棒！问题反过来是否也成立呢？大家看一下变式3.

变式3 若A，B是抛物线y2=2x上异于顶点O的两动点，且满足OA⊥OB，试问：AB恒过定点吗？

师：大家尝试一下.(几分钟后)

师：谁愿意来展示一下？

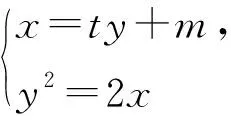
师：很好，请大家再观察一下定点(2,0)与抛物线的方程y2=2x有什么关系呢？

生9：定点(2,0)中的横坐标，恰巧是抛物线的方程y2=2x中的2p.然后我们小组进行了猜想如下：已知A，B是抛物线y2=2px(p>0)上异于定点O的两动点，满足OA⊥OB，直线AB恒过定点(2p,0).

师：完成的非常漂亮！那么我们现在是否可以初步下这样的结论：“当满足OA⊥OB时直线AB恒过定点”.

设计意图：通过对课本习题的多角度探索，得到解决这一类问题的通法，同时注重方法的提炼与优选，渗透特殊值法、转化的思想，也为得到一般结论做铺垫.

2.3 片段三：一般推广，一深化理解

变式4 已知A，B是抛物线y2=2px(p>0)上异于定点O的两动点，满足OA⊥OB，证明：直线AB恒过定点(2p,0).

师：哪位同学来展示一下.

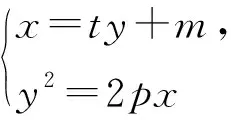
师：真棒！如果将变式4的条件与设问调换是否同样成立呢？大家动手探索一下.

变式5 已知A，B是抛物线y2=2px(p>0)上异于定点O的两动点，若直线AB恒过定点(2p,0)，证明：OA⊥OB.

师：哪位同学来展示一下.

设计意图：通过发散思考，把具体的抛物线得到结论推广到一般情况，加深理解.

师：如果把抛物线上特殊定点O改为一般的定点结果将会怎么样呢？大家请看变式6.

2.4 片段四：类比迁移，拓展延伸

变式6 过抛物线y2=2x上的点M(2,2)，作直线MA⊥MB交抛物线于A，B两点，是否存在直线AB恒过定点，若存在，请求出该定点，若不存在请说明理由.

学生用上述解题方法和经验，解出定点为(4,-2)，教师鼓励学生大胆猜想，然后求证.

师：谁来展示？

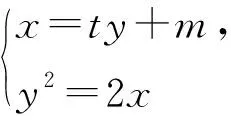
师：非常好！大家探索一下是否存在更一般化的结论，大家试求证一下变式7.

变式7 过抛物线y2=2px(p>0)上的一点M(x0,y0)作两条互相垂直的直线与抛物线交于A，B两点，如图1.证明：直线AB经过定点N(x0+2p,-y0).

图1

师：哪位同学来展示一下？

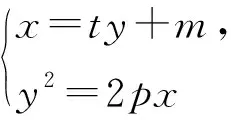
师：太棒了！还有其它解法吗？

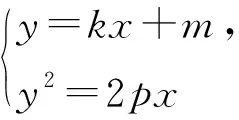
师：这两位同学非常优秀！这样我们得到这样的结论：“过抛物线y2=2px(p>0)上的一点M(x0,y0)作两条互相垂直的直线与抛物线交于A，B两点，直线AB经过定点N(x0+2p,-y0)”.

设计意图：从具体到一般，从抛物线顶点的特殊位置到一般位置，这样由浅入深，由表及里，搞清楚了该类直线恒过定点的性质，使知识体系化.同时变式6让学生进一步熟悉直线恒过定点的开放性问法.

2.5 链接课本和高考

链接1 (选修4-4第33页例3探究)在例3中(O是直角坐标原点，A，B是抛物线y2=2px(p>0)上异于顶点的两动点，且OA⊥OB)，点A，B在什么位置时，△AOB的面积最小？最小值是多少？

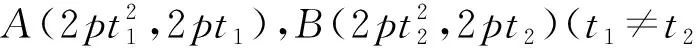
采用今天方法的解答，过程如下:

链接2 (2017年全国3卷理科20题)已知抛物线C:y2=2x，过点(2,0)的直线l交C于A，B两点，圆M是以线段AB为直径的圆.

(1)证明：坐标原点O在圆M上；

(2)设圆M过点P(4,-2)，求直线l与圆M的方程.

设计意图：把分散在课本中例题、习题、高考真题聚结串联起来，形成知识链，加深对一类问题的深刻理解，并且通过对课本题源的挖掘、引申、拓展，展现高考题的命题过程和思路轨迹，让学生看到教材上例题、习题与高考题之间的内在联系，消除了学生对高考试题的恐惧感和神秘感，同时帮助学生构建知识，掌握方法.

3 教学反思

3.1 后期备考思考

高三后阶段复习，要回归基础、回归教材，设计低起点的课本习题为切入点，旨在激励更多的学生参与课堂活动，营造良好的学习氛围，为后续的课堂教学做好铺垫.然后通过温和的变式，变式之间思维跨度不宜过大，综合度不宜过高.一般从特殊情形出发，逐渐改变某些量得到一连串相关的变式题，最后触及问题的内核，构建深度教学，引领学生深度学习.在此过程中，加深学生对数学“四基”的理解与掌握，提升数学“四能”发展数学素养.

3.2 复习教学要重视“导”

本节课所选的教材习题并没有直接提到直线定点问题，但通过教师的引导将学生目光聚焦本节课的核心问题.教师科学的设计教学环节，通过改变定直线的斜率、过定点到一般直线，从特定曲线到一般曲线，从曲线上的特殊点到一般点学生经历了从特殊到一般的研究过程，尔后教师引导学生分析：问题在变式过程中弄清变化的因子和不变的本质，从而得到一般的结论，再到链接课本和高考，让学生体会发现问题，探究新知，应用知识解决问题的愉快过程.教学过程由浅入深、层层递进，符合学生的元认知水平，提高学生参与课堂活动的积极性，又通过问题驱动为教学开展注入了活力，整个教学过程教师很好的做到了教师是主导学生是主体的课堂角色，教学效果显著.

3.3 挖掘教材例题、习题

高三数学复习教学没有教材，可以根据所教学生的认知特点以及心理规律和学生当前的数学基础与数学能力等实际情况，全面研究课标、研究考纲、研究考题、研究教材例题，有机整合教材例题、习题.在尊重教材例题、习题的基础上，对教材例题、习题进行推广、变式、类比探究、改编等方式方法激活教材例题、习题，编写复习材料.可以将教材例题、习题原先主要用来巩固知识、深化概念理解的知识立意改编成突出能力立意，突出数学思想方法的学习；可将教材例题习题的单纯解答问题改编成突出回顾复习知识，建构知识体系，巩固知识结构；可将教材例题、习题“结构良好”的封闭题改编成“思维发散”的开放题，如：探究型存在性问题、探索性问题、归纳猜想和演绎证明等问题，创造性的使用教材例题、习题，让教材例题、习题更好地发挥其教学作用.