一道椭圆最值问题的解法探究

江苏省苏州市第四中学 (215000) 甄 艳

圆锥曲线是高考数学核心考点之一，而最值问题是热点题型之一，最值问题主要考查直线与椭圆的相交关系和圆锥曲线的几何性质，这类问题对考生的运算求解能力、推理论证能力和综合思维能力要求较高.以下对一道椭圆有关的最值问题进行多解探究.

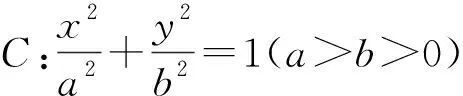
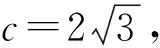
(2)思路1：设出直线方程，联立椭圆方程，由弦长公式表示|MN|，再由点到直线距离公式表示点A到直线的距离，用k表示出△AMN的面积，对k分类讨论，最终由基本不等式和不等式性质可求出△AMN面积的最大值.

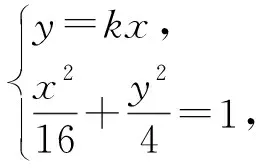
当k>0时，S△AMN<4，当k<0时，S△AMN=

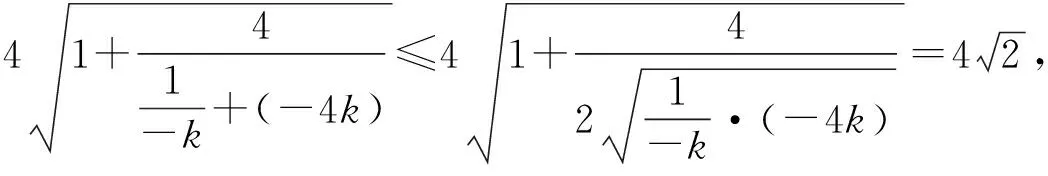
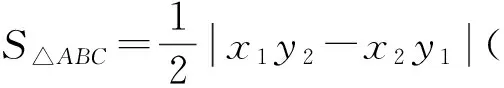
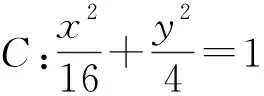
思路3：设出点M的坐标，利用已知条件表示出点N的坐标，利用解法2中提到的三角形面积公式表示出△AMN的面积，再利用点M在椭圆上实现整体代换，利用均值不等式a2+b2≥-2ab和不等式性质可求出△AMN的面积的最大值.

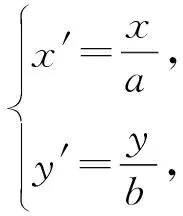
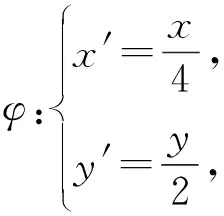
评析：解法1运用了分类思想，运算量比较大，如果考生的运算和推理能力不强，很难得出最终结果，解法2运用了参数方程法，运算量明显减少，问题化归为与三角函数有关的最值问题，解法3对综合思维能力要求高，整体代换思想和均值不等式的应用具有创新性，解法4利用伸缩变换“化扁为圆”，将问题化成圆中考生比较熟悉的问题，运算量较少，但思维层次比较高，需要教师将教材中比较基础的伸缩变换知识进行拓展.