例析利用导数求解三角问题

广东省梅州市虎山中学 (514299) 张伟荣 江中伟

本文在导数视角下研究三角函数的单调性、奇偶性、对称性、最值问题、含参问题或相关综合性问题的求解策略.

一、利用导数研究三角函数的单调性问题

例1 (2018年全国高考数学Ⅱ卷第10题)若f(x)=cosx-sinx在[-a,a]上是减函数，则实数a的最大值是( ).

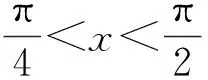
反思总结：由导数与函数单调性的关系可知，若函数f(x)在(a,b)上单调递增，则f′(x)≥0；若函数f(x)在(a,b)上单调递减，则f′(x) ≤0.当涉及到含参数的三角函数在某个区间上单调求参数的取值范围时，可求导后采用分离参数的方法.

二、利用导数研究三角函数的奇偶性问题

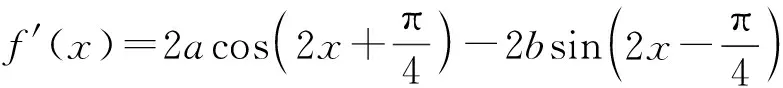
例4 若函数f(x)=sin(x+θ)+cos(x+θ) (0<θ<π)是奇函数，则实数θ=.

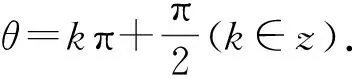
三、利用导数研究三角函数的对称性问题

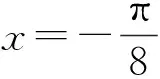
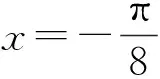
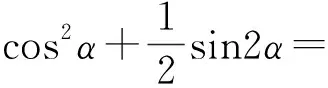
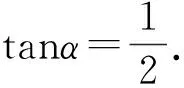
反思总结：利用可导函数在极值点(最值点)处的导数为零求解.

四、利用导数研究三角函数的最值(极值)问题

例7 (2013年全国卷理科第12题改编)已知函数f(x)=cosxsin2x,求f(x)的最大值.

反思总结：通过三角恒等变形后换元，构造一个新函数(注意变量的取值范围)，求导，判断单调性，求最值(极值).

五、利用导数研究三角函数的零点问题

(1)求函数f(x)与g(x)的解析式;

分析：(1)由已知条件易得f(x)=cos2x，g(x)=sinx(过程略).

反思总结：这道题充分体现了利用导数研究三角函数零点的优越性，第二问主要考查了等差数列、函数零点存在定理、导数和不等式等基础知识，体现了对数学抽象、逻辑推理、数学运算等数学核心素养的考查.