促进自然生成 凸显数学本质
——以“三角函数的概念”教学为例
浙江省湖州市滨湖高级中学 (313000) 郑梦华
浙江省湖州中学 (313000) 祝峰泽
数学教育基本理念是“以学生发展为本,立德树人、提升学生核心素养,培养学生的科学精神和创新意识,实现不同的学生得到不同的发展,培养具有终身学习能力并适应社会需要的人才”,数学本质实际上是指数学知识的内在联系、数学规律的形成过程、数学思想方法的提炼以及数学理性精神的体验,教师通过问题驱动引导学生在课堂中通过活动探究分析、解决问题,学生在活动探究过程中,通过亲身体验数学知识的形成过程,体会到数学知识的理性精神与科学精神,并在知识的探索过程中逐步摸索其中蕴含的数学思想方法、数学研究工具,掌握并理解数学本质,提高学生终身学习能力,最终实现学生个人的发展.因此,数学教学中通过问题驱动让学生知识自然生成中掌握数学本质不失为一个有效又合理的教学方法,该教学模式也能为当下数学教育改革寻找一个新路径.
笔者对“三角函数的概念(人教A版2019)”一课进行课堂实录,节选部分教学片段进行分析评价,教学过程中主要通过问题驱动引导学生进行活动探究、独立思考等让学生在课堂中掌握理解三角函数概念的数学本质,体会其中蕴含的数学思想方法、数学规律,体验数学知识的生成过程及数学的理性精神,加深学生对三角函数的概念的理解,培养学生的学习能力,从而实现学生的素养发展.
1 课堂实录(节选片段)
1.1 在活动中提炼数学思想方法
提出问题:让学生以三人一组为单位,组号记为A、B、C等,每一组任意画一个锐角,记作角α、β、γ等,借助三角板,各自求出该锐角的正弦值、余弦值和正切值的近似值.
学生回答如下表:(投影仪展示,此略)
师生活动:师生一起了解三角函数的数学史,了解数学史中三角函数定义——线段比.
设计意图:让学生对不同的锐角以及同一个锐角运用不同的线段比去计算三角函数值,从一般的锐角三角函数值计算中体会到其线段比的数学本质定义,及数学史的角度.学生能够从中体会到相同的定义,提炼了从一般到特殊的思想方法,为学生后续运用数学思想方法进行学习打下深厚的基础.并且学生是在自己的活动经验中进行体会,学生对数学思想方法的理解和运用能够更加深刻.
1.2 在思考中体会数学规律
提出问题:大家所求的锐角三角函数值有何特点呢?
学生回答:角的大小确定时,对应的锐角三角函数值差不多相等,为该角所在的直角三角形中线段长度的比值.
提出问题:与你们找的点所在的位置有关吗?
学生回答:无关.
提出问题:既然锐角三角函数值与点A所在的位置无关,那你们能否找到一个点A,使锐角三角函数值计算更简洁呢?
设计意图:这一过程教师是通过三个问题引导学生思考,有何特点、是否有关、如何更简洁等问题,通过一连串精简的提问,给学生充足的思考时间让学生发现任意的锐角三角函数值的共同特征是线段比这一数学规律,以及三角函数中可以运用单位圆这一研究工具使问题更简便,学生在自己的独立思考之中领悟数学知识中蕴含的数学规律,学生能够对规律的形成以及理解更深刻,后续的使用也能更得心应手,同时学生在思考过程中的体验都能给学生后续学习提供一些帮助.
1.3 在已有的数学现实上建构新知
提出问题:既然锐角三角函数值sinα只与角α有关,那么sinα和角α有什么关系呢?
学生回答:(生1)三角关系;(生2) 函数关系.
提出问题:α是一个数吗?
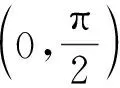
设计意图:高中数学由代数、几何、统计与概率几个模块内容展开,而函数是代数的一个重要主线,三角函数又是函数的一个重要分支,如何将锐角三角函数值过渡到三角函数,让学生能够从函数的角度研究三角函数值,这对于学生来说是一个质的变化,在这一过程,教师通过提问式,让学生对自己的回答与他人的回答进行反思,并在反思与猜想中与自己已有的数学现实进行联系,对已有的知识系统进行重新建构,发现在角度与锐角三角函数值之间也有一种特殊的关系,而这种特殊的关系正符合函数的定义,在这一过程中,学生是自己通过猜想论证过程得到三角函数的函数本质,而不是教师直接告知学生锐角三角函数也是一个函数的,学生能够通过对自己知识系统进行联想,再创造发现锐角三角函数的函数本质,这种学习方式也能为学生后续学习三角函数的概念、性质等奠定基础.
1.4 运用数学工具得到数学概念
提出问题:既然sinα是一个函数,自变量是锐角α,那如果角α为其他角度时,是怎样的呢?
学生回答:(生1) 在平面直角坐标系作角(弧度制是在平面直角坐标系中研究得到);(生2)随便作一个角.
提出问题:如果角α为其他任意角时,此时角α与sinα的定义是怎样的?
师生活动:学生利用已有经验作任意角,教师则运用几何画板作可以转动的任意角(以原点O为角的顶点,以x轴正半轴为角的一边OB,转动另一边,表现任意角),随后学生之间进行交流探索,得到以下几种不同结果.

学生回答(随意作任意角):运用直尺作直角三角形,度量长度得到三角函数值.
提出问题:你们觉得自己所作的角能清晰明了地表现三角函数值与角的关系吗?如何作角才能简洁明了地体现三角函数的特征?

设计意图:教师通过问题引导学生将锐角拓展到任意角,任意角如何表示及其三角函数如何定义是这一教学过程的重难点,首先让学生自己作出任意角,教师用几何画板作角,此时学生作角有各种情况,但是当他们在求所作角的三角函数值时,学生发现三角函数值求解较复杂,此时让学生进行对比讨论,学生发现将直角三角形与平面直角坐标系、单位圆相结合时,运用单位圆及坐标能够简洁明了地表示出角的三角函数值,单位圆与平面直角坐标系的教学工具是学生自己发现的,由锐角到任意角,始终抓住三角函数原始定义线段比,运用单位圆,实现由几何定义法——终边定义法——单位圆定义法得到最简洁的三角函数的定义,学生在这个过程能够对三角函数的概念有一个深刻的理解和认识,并且始终是学生去寻找工具、发现概念,由此发挥了“以学生为主体”的教学思想,并且在三角函数的概念获得的过程中凸显了数学工具的重要性,也为学生后续学习选择合适的数学工具、数学方法提供了一些经验.
2 感悟结语
通过本节课的教学,我们认为数学本质是数学学习的核心,在数学教学中教师应瞄准学生如何“学”,让知识不再是直接呈现给学生,而应让学生参与到课堂,唤醒学生的思考能力,让学生在探究思考的过程中能够了解知识的生成过程,体会到数学学习的方法、工具,从而培养学生的学习能力.

