一道美国数学奥林匹克题的八种证法
广东省深圳中学 (518001) 邱际春
题目如图1,BE、CF分别是锐角△ABC的两条高,以AB为直径的圆与直线CF相交于点M、N,以AC为直径的圆与直线BE相交于点P、Q.证明:M、N、P、Q四点共圆.(第19届美国数学奥林匹克第5题)
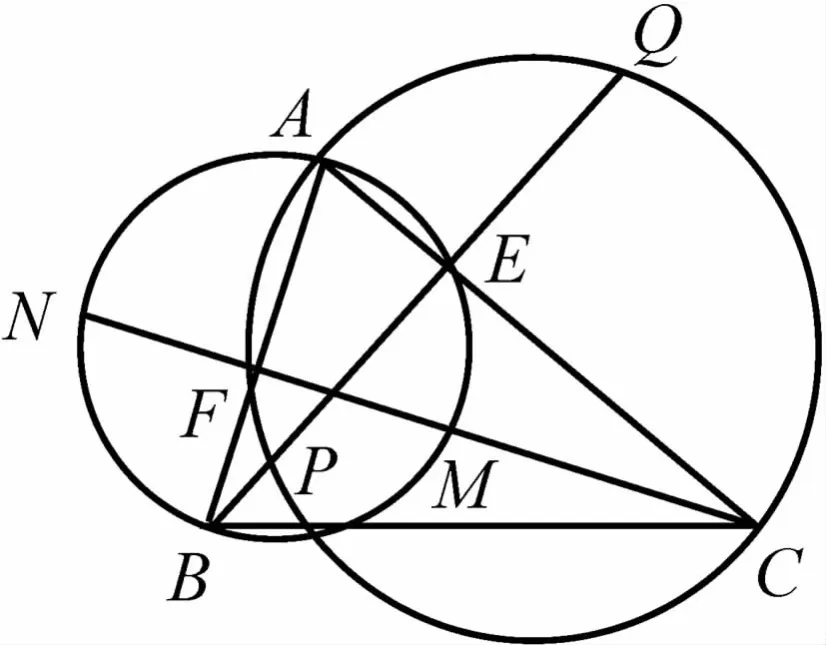
图1
从图形结构来看,此题条件精炼,结构优美,解法丰富.文[1]利用线段间的数量关系结合相交弦定理对此赛题进行了证明,文[2]分别运用三角法和解析法给出两种证法,笔者在文[3]中利用反演变换给出这一赛题的新证法,并在文[4]中通过类比和改造图形结构演绎出一些新结论.
本文从图形特征出发,利用相似三角形的性质、圆的有关性质和定理及三角代换等技巧,从而给出下面八种新的证明方法,以飨读者.
1 利用相似三角形的判定与性质证明


图2

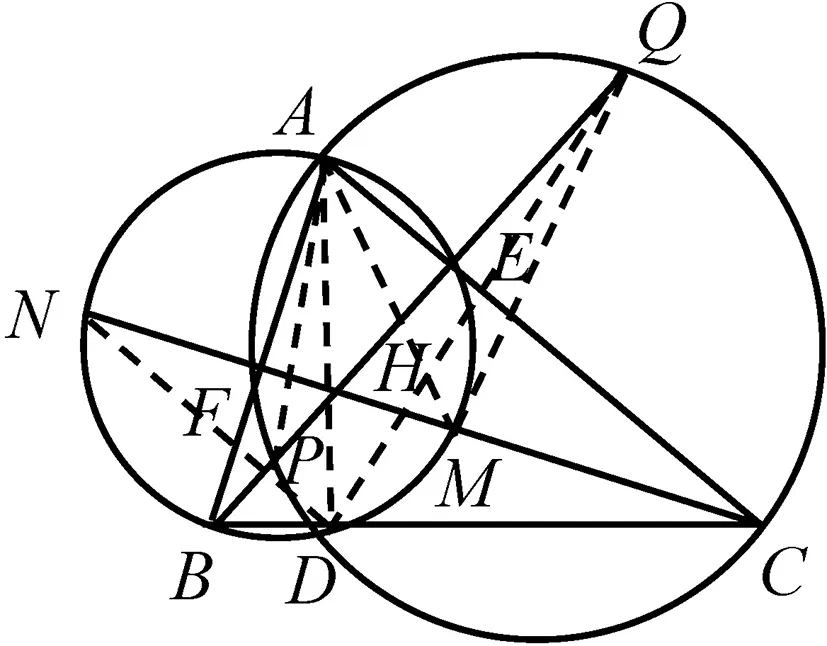
图3
评注:事实上,利用相似证明M、N、P、Q四点共圆的方法有很多,中学阶段最为常用的方法是通过证得共底边的△PHN的顶角∠PNH和△MHQ的顶角∠MQH相等,且在底边同侧,从而推出四个顶点共圆.
2 利用圆幂定理及其逆定理进行证明
证法三:如图4,设BE、CF交于点H,由题设条件知H为垂心.连接AH,且延长后交BC于点D,则AH⊥BC,即∠ADB=∠ADC=90°.又因为AB和AC分别是两圆的直径,所以点D是两圆的交点,故由相交弦定理可得MH·HN=AH·HD=PH·HQ.因此,M、N、P、Q四点共圆.
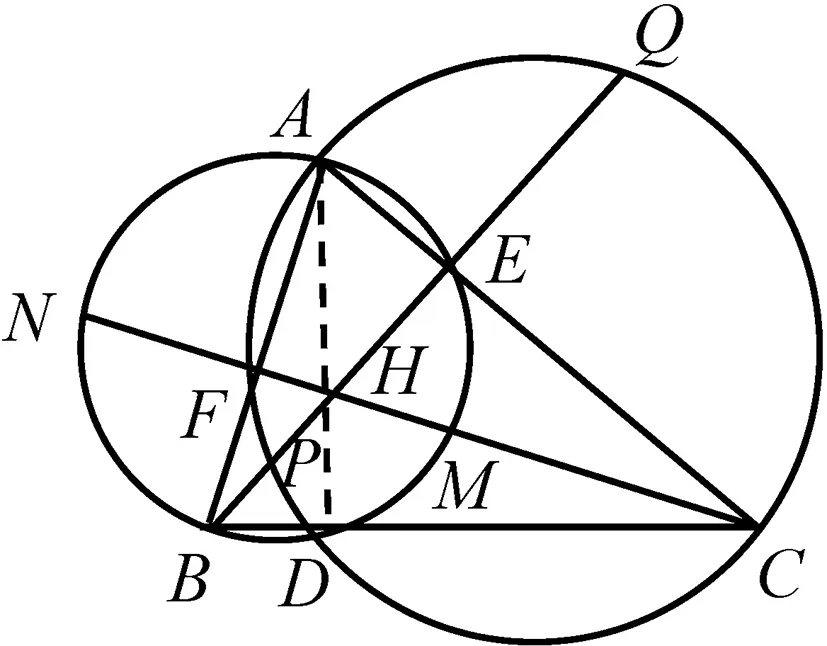
图4
证法四:如图5,因为BE、CF分别是锐角△ABC的两条高,所以∠CFB=∠CEB=90°,所以B、C、E、F四点共圆.又因为AB和AC为两圆的直径,所以点E和点F均为圆上的点.注意到B、M、E、N,P、Q、C、F均为四点共圆,故利用相交弦定理可得MH·HN=BH·HE=CH·HF=PH·HQ,故M、N、P、Q四点共圆.

图5
评注:相交弦定理和切割线定理统称为圆幂定理,注意到MH·HN、PH·HQ分别是两圆的幂,要证M、N、P、Q四点共圆,则需要证明点H是两圆的等幂点.这就需要反复用到圆幂定理,它在数学竞赛中是证明四点共圆的有效工具.
证法五:因为BE、CF分别是锐角△ABC的两条高,所以∠CFB=∠CEB=90°,所以B、C、E、F四点共圆.如图6,连接AM,AN,AP,AQ,则由垂径定理知AM=AN,AP=AQ,下面只需证AM=AP.利用圆幂定理可得AF·AB=AE·AC,又因为AB和AC为两圆的直径,所以∠AMB=90°,∠APC=90°.由射影定理可得AM2=AF·AB,AP2=AE·AC,故AM=AP.因此,M、N、P、Q四点共圆.
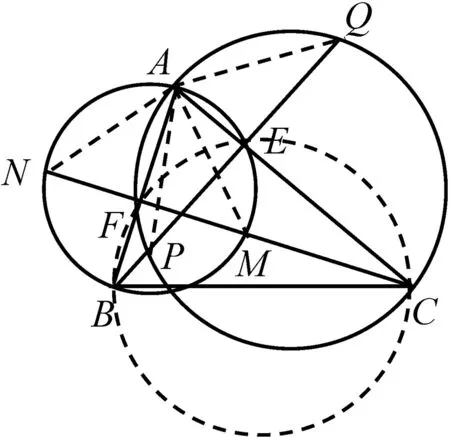
图6
评注:注意到MN⊥AB,PQ⊥AC,根据垂径定理知AM=AN,AP=AQ.于是容易想到点A为所证圆的圆心,并证明这四个点到它的距离相等.
3 利用定差幂线定理进行证明
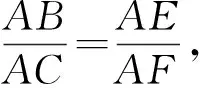

图7
评注:上述证明过程中用到了一个重要的结论:AH⊥BC等价于AB2-HB2=AC2-HC2.这个结论称为定差幂线定理,它是证明垂直这一类问题的常用方法.
4 利用根轴的性质进行证明
证法七:设BE、CF交于点H,由题设条件知H为垂心.如图8,连接AH,且延长后交BC于点D,则AH⊥BC,即∠ADB=∠ADC=90°.又因为AB和AC分别是两圆的直径,所以点D是两圆的交点,AD为两圆的根轴,故点H到两圆的幂相等,即MH·HN=PH·HQ.因此,M、N、P、Q四点共圆.

图8
评注:由于AD、CF、BE分别是⊙ANBM、⊙APCQ和⊙BFEC两两的根轴,故点H是三圆的根心.
5 利用三角函数法进行证明
证法八:如图9,分别连接AH,AM,AP,BM,CP,设△ABC的外接圆半径为R,则由题意知CN⊥AB,BQ⊥AC.因为AB和AC分别是两圆的直径,所以FM=FN,EP=EQ,∠AMB=∠APC=90°.由射影定理得PE2=AE·EC,MF2=FA·FB.由于∠AHE+∠HAE=90°,∠HAE+∠ACB=90°,可得∠AHE=∠ACB,故EH=AHcos∠ACB=2Rcos∠BACcos∠ACB.同理可得FH=2Rcos∠BACcos∠ABC,所以要证M、N、P、Q四点共圆,等价于要证MH·HN=PH·HQ.由正弦定理可得MH·HN=(MF-FH)(MF+FH)=FA·FB-FH2=BC·AC·cos∠BACcos∠ABC-4R2cos2∠BACcos2∠ABC=4R2cos∠BACcos∠ABC(sin∠BACsin∠ABC-cos∠BACcos∠ABC)=-4R2cos∠BACcos∠ABCcos(∠BAC+∠ABC)=4R2cos∠BACcos∠ABCcos∠ACB,同理有PH·HQ=(EP-EH)(EP+EH)=EA·EC-EH2=BC·AB·cos∠BACcos∠ACB-4R2cos2∠BACcos2∠ACB=4R2cos∠BACcos∠ACB(sin∠BACsin∠ACB-cos∠BACcos∠ACB)=-4R2cos∠BACcos∠ACBcos(∠BAC+∠ACB)=4R2cos∠BACcos∠ACBcos∠ABC,故MH·HN=PH·HQ.因此,M、N、P、Q四点共圆.

图9
结语:事实上,文[4]以源问题为起点,基于纵向分析和改造几何结构,进而演绎发展出一系列的新结论.本文则从横向视角,通过对这一优美的两圆模型进行较为深入的解题探索,让我们从不同的角度重新审视该问题,也让我们感受到几何纯粹的内在美与它富于神奇的变化.在浩如烟海的数学竞赛题中,几何试题千变万化.若能跳出问题本身来看待问题,从而探究延伸出新问题,或提炼出这类问题的经验方法和解题策略,这无论是对于解题能力的提升,还是对于命制新颖的试题,都是大有裨益的.

