基于节点状态变化的社区检测算法

蔡威林，葛 斌

（安徽理工大学,计算机科学与工程学院，安徽 淮南 232000）

近年来，各领域的大量科研人员投入到对网络学科的深入研究中，社会网络[1]、电商网络[2]、生物网络[3]、电力网络[4]等都是复杂网络的例子。网络社区检测作为复杂网络研究的一个重要方向,越来越引起研究者的关注[5]。

复杂网络中，节点通过边连接成成对，一些节点相对紧密地连接在一起并聚集成簇或堆，这就是所谓的社区结构[6]。随着社交网络中数据复杂性逐渐增大，网络中节点之间的相关性逐渐增加，同一社区的节点通常具有相似的属性[7]和特征[8](如背景、职业或兴趣)，社区结构逐渐复杂，社区检测变得及其困难。传统的计算方法，例如：GN算法[9]，FN算法[10]，LPA算法[11]，无法满足现有网络的检测计算，需要新的方法解释网络中两个节点之间的相似程度，从而划分出相应的社区，对节点加以区分。

1 相关工作

近年来，许多学者对节点相似性开展了深入研究。例如，文献[12]提出基于相似度的动态演化符号，加入最短路径使得相似度随着时间变化。文献[13]提出的IES算法,它基于信息熵和余弦相似度，以节点对社区的相似度进行判别。文献[14]提出FCSL算法，它把余弦相似度和共享连接相结合寻找节点相似性。文献[15]提出LPA-S算法，在标签传播过程中将公共邻居考虑进节点间的相似度计算，标签跟随相似度传播。文献[16]提出一种局部相似性度量，并结合层次聚类用于社区结构发现，克服了传统局部相似性度量在某些情形下对节点相似性的低估倾向。文献[17]引入相似度来衡量节点间连接强度，改进具有高影响力的种子节点选取方法，提高了社区检测算发的准确度。文献[18]提出CDASS算法，通过定义公共邻居相似度，划分节点在社区结构中位置，将相似节点分配给同一社区。文献[19]提出了一种新的基于非负矩阵分解和图优化的网络社区检测算法根据属性配置文件构造了节点的属性相似矩阵。文献[20]提出了根据不同的邻居节点类型分配不同的边缘权重影响因子来计算节点相似性。

现阶段的研究虽然结合相似度的方法进行判断节点社区划分，但都没有考虑节点状态变化。根据文献[21]提出在民航网络中引入节点状态可以提高网络安全运行，文献[22]提出将实时节点状态运用在物联网节点中，提高节点有效检测范围，发现加入节点状态因素在网络数据可以更好的分析网络。因此，节点状态的变化可以考虑在节点相似度的计算中。网络中节点的状态取决于其邻居的当前状态，并且每个节点的状态只能在两种状态中选择:0 和1。0 表示节点未激活，1 表示节点已激活。因而我们可以为每个节点定义一个称为变化指数的量，如下所示:

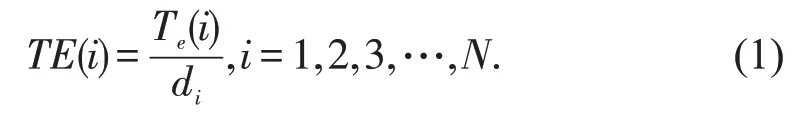
其中Te(i)表示节点vi的邻居中状态为1的节点数，di表示节点vi的度。

本文提出一种基于节点状态变化的社区查找方法，并将其称为动态相似度算法(TCS)。在开始定义了变化指数，然后计算节点邻居和自身的相似性，最后结合余弦相似性理论完成社区查找。

2 相似度算法

假设网络模型可以表示为G=（V，E）.包含N个节点和M条边的连通网络其中V={v1,v2,v3,…,vN}表示节点集，E={e1,e2,e3,…eM}是边集。我们利用邻接矩阵来描述网络的连接模式。节点vi和vj之间的连接强度由矩阵a的元素(Aij)表示。i,j是V中任意的两个节点，当两个节点直接相连时Aij=1,否则Aij=0。

2.1 余弦相似度

早期常用的相似性度量包括Jaccard 相似性、余弦相似性和RA 指数。余弦相似性是是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。余弦值越接近1，就表明夹角越接近0 度，也就是两个向量越相似。对于节点vi和vj,其相似性公式如下：

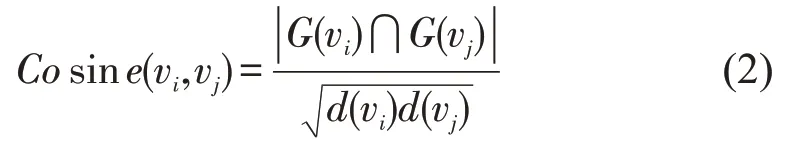
其中G(vi)和G(vj)表示节点vi和节点vj的邻居集,d(vi),d(vj)表示节点vi，vj的度。相似性度量范围从0 到1。

以往的以余弦相似度为代表的相似性度量方法有效地解决了相邻节点的问题，计算对象间的距离，用于数据聚类，但不能准确、全面地管理节点与节点之间的关系。为了得到更准确的划分结果，本文提出了一种基于节点状态变化的方法，作为节点间相似程度的度量方法。

2.2 节点相似性

首先，每个节点都可以假设为源节点，而邻居节点会根据节点状态的变化进而产生不一样的时序影响，故我们需要考虑到节点自身和其邻居节点在时间段的总体变化，因此定义一个计算节点的所有邻居的影响称为节点变化指数。其公式如下：

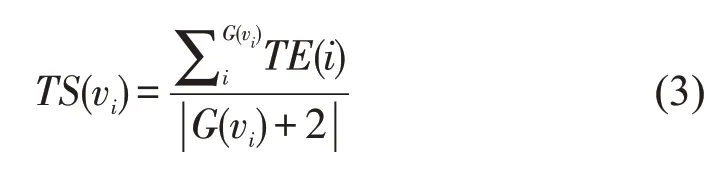
其中，G(vi)表示节点vi的邻居节点集合，TE(i)表示节点vi的变化指数。

其次，在社交网络中选择源节点，源节点可以影响其邻居节点，最后到达整个网络。我们选择一个节点作为源节点，可以根据节点状态变化计算节点之间的相似度。因此，在余弦相似度的基础上结合基于节点变化指数的结果，本文定以了一个节点之间的相似性度量称为动态节点相似度，其公式为：

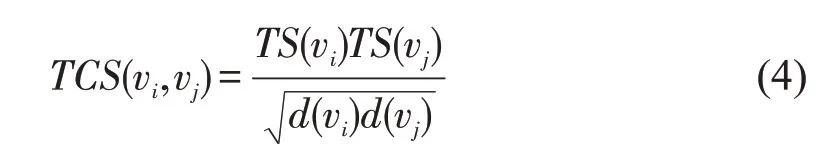
其中，TS(vi）表示节点变化指数，d(vi),d(vj)表示节点vi，vj的度。

上述计算过程描述如下：

Step1:输入一个网络G=(V,E)；

Step2:根据公式(1)产生N 个不同的变化指数TE；

Step3:根据公式(3)计算每一对节点之间的节点变化指数TS；

Step4:根据公式(4)计算每一对节点间的动态相似度TCS；

Step5:删除当前网络相似度最低的边;

Step6:根据公式(5)计算当前网络的模块性Q和标准归一化NMI;

Step7:重复2-6 操作，直到当前网络模块性Q或标准归一化NMI 最大；

Step8:输出当前网络的社区划分。

算法过程中，首先计算每对节点之间的动态相似度，然后删除网络中相似度最低的节点对的边。把模块性Q 和标准归一化NMI 作为当前网络划分的标准，重复上述删除边的操作，直到模块性Q 或标准归一化NMI 取得最大值。最后停止计算，输出当前的社区划分，并记录模块性Q 或标准归一化NMI的值。对于模块性Q 或标准归一化NMI 会在3.1 小节详细介绍。

3 实验

本文使用的社交网络包括空手道俱乐部网络(Karate)、海豚俱乐部(Dolphins)、美国大学生2000赛季美式足球联赛网络(Footballs)、美国政治书籍网络(Books)通过所提出的相似性度量来寻找数据集中的社区结构，得出社区划分结果。然后根据测量标准模块性(Q,Modularity)值和标准归一化(NMI,Normalized Mutual Information)值进行评估，从而判断其性能。作为比较，我们还将几种经典的社区检测方法应用于上述数据集。

3.1 评价指标

1.第一个评价指标为模块性(Q)，它是评价社区检测的经典方法，被广泛采用来表示特定分区的社区结构的强度，以此用来衡量社区划分的好坏。因此，Q的值越大说明社区的结构越清晰。形式上，模块性（Q）可以定义为：

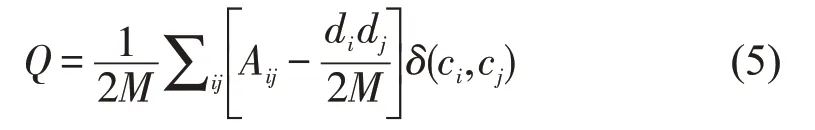
其中，di，dj表示节点vi,vj的度数，如果节点vi,vj在同一个社区，则函数(ci,cj)等于1，否则函数等于0。当所有节点都归属同一个社区的时候，Q=0。

2.第二个评价指标为标准归一化(NMI)。在社区检测问题中，标准归一化可以检测社区和真实社区之间的相似性。考虑两个分区A={A1,…,Aa}，B={B1,…,Bb}并使用C来表示混淆矩阵。该矩阵的每个元素Cij表示同时属于团体A共和团体B的公共节点的数量。形式上，NMI 定义为：

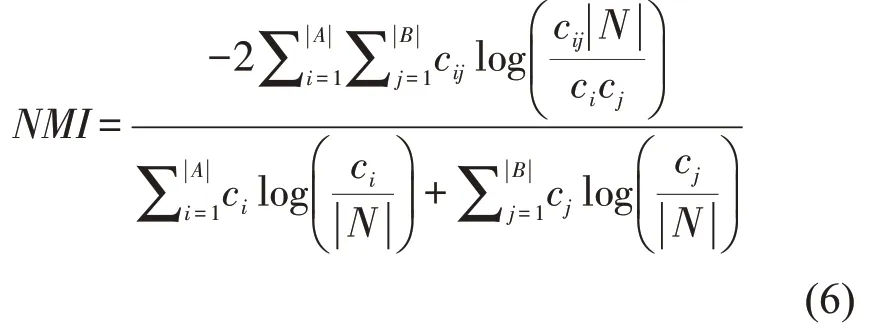
其中|A|和|B|分别是分区A 和B 中社区数。Ci和Cj分别表示矩阵的第1 行元素之和和第1 列元素之和。当一个网络的两个分区相同时，我们有NMI=1,两个分区完全独立时，NMI=0。

3.2 实验结果与分析

在四个数据集上分别对LPA、GN、FN、TCS这四种算法进行实验，计算模块性Q 和标准归一化NMI 并对实验结果进行综合评估与分析，实验结果得到的数据如表1 所示。

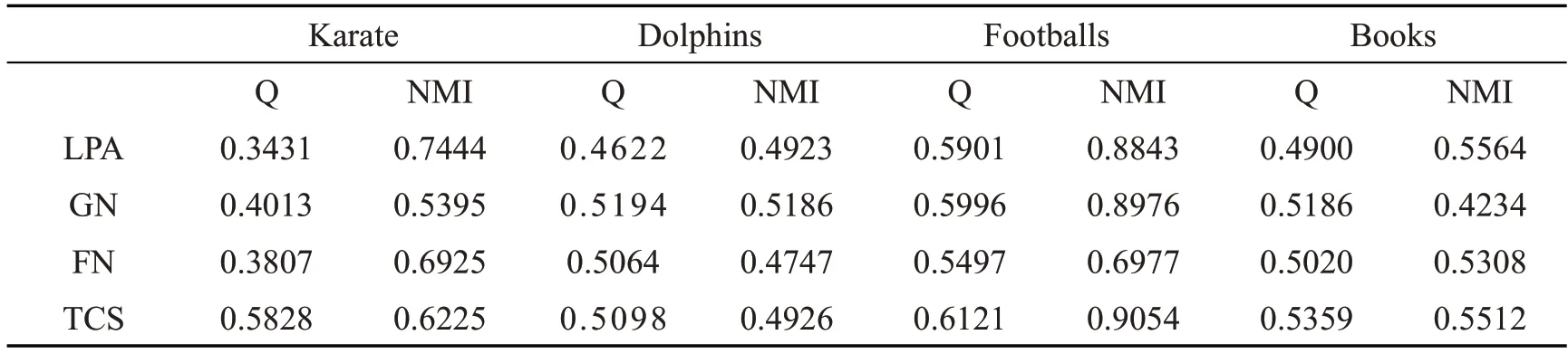
表1 各算法在数据集下的模块性和NMI的值

图1 为各算法模块性结果详细对比情况，可以看到TCS算法在Karate、Footballs、Books 三个数据集下模块性Q的值均高于经典算法，说明TCS算法确定社区划分得到的社区结构更加清晰。而在Dolphins 数据集中节点与边比值较大，GN算法的边介数计算方法比TCS算法的动态节点相似度更容易分析网络，故GN算法取得的值较高。但总的来说，TCS算法的模块性还是高于经典算法的，说明其可以发现更加清晰的社区结构。

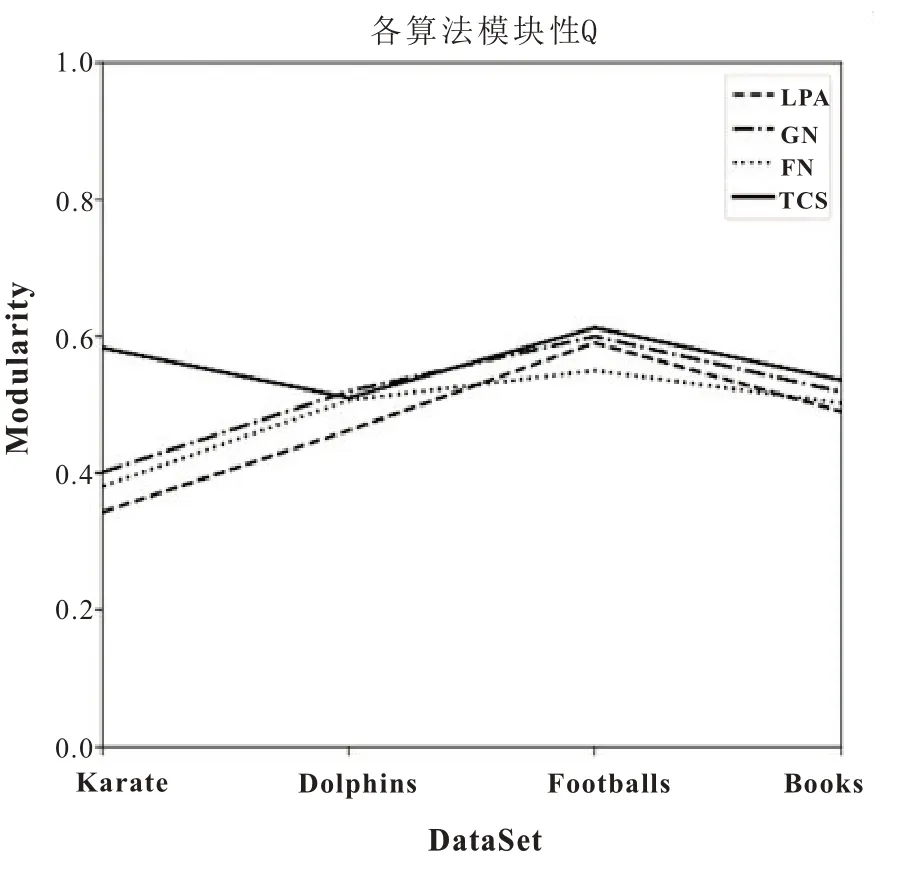
图1 各算法模块性Q

图2 为各算法标准归一化NMI的值详细对比情况，可以看到TCS算法在四个数据集下标准归一化NMI的值与经典算法的值是非常相近，因为TCS算法与其他经典的算法相比，都是通过删除边的操作来进行社区划分，最后得到的社区情况相差不大，故各算法的值都非常相近。但总的来说，TCS算法的划分社区和真实社区还是有较高的相似度，且丝毫不弱于其他经典算法。

图2 各算法标准归一化NMI

4 总结

本文提出了一种新的网络节点对相似性度量方法。以往的研究考虑了相似性在社交网络中的应用，但是都没有考虑到节点状态变化使节点相似性发生变化。基于节点状态变化对相似度的影响，定义变化指数(TE)来表示网络中节点变化，通过节点变化指数(TS)来定义网络节点之间的总体变化。在此基础上，结合余弦相似度得到动态相似度算法(TCS)来表示网络中节点之间的相似度。我们将所提出的算法应用于社交网络，比较评价指标模块性Q 和标准归一化NMI，实验结果表明TCS算法取得的社区划分效果均优于经典算法，得到了社区结构强度更高，与真实社区更相似的社区划分。因此，验证了提出TCS算法的有效性,证明基于节点状态变化的社区检测是可行的。

本文研究的都是无向网络，而现实不仅存在无向网络，更是存在着有向网络。在将来，我们将致力于推广我们处理有向网络的方法，探索节点状态对于有向网络社区检测的意义。