卷积等价分布族的封闭性
高 宇,杨月丽,彭 千
(1.安徽大学 数学科学学院,安徽 合肥 230601;2.安徽农业大学 理学院,安徽 合肥 230036)
1 引言
卷积等价分布族是应用概率论中一类重要的分布族,同时该分布族由于其良好的性质现已广泛应用于排队论[1]和风险理论[2]等领域。对于卷积等价分布族的研究可见文献[3-13],近期应用可见文献[14-15]。然而,在卷积等价分布族的诸多研究中,最基本问题还是其在卷积运算下是否具有封闭性。Kluppelberg 和Villasenor 较早得到该分布族不满足封闭性,并且给出了相应的反例[16]。因此,寻找在何时条件下卷积等价分布族关于卷积运算具有封闭性一直是应用概率统计学者关心的问题,但由于数学方法上的局限性,关于该问题的研究进展缓慢。直到2020 年,Leipus 才首次给出了卷积等价分布族关于卷积封闭的若干充要条件[17]。这显然是一个非常重要的理论研究成果,在卷积等价分布族的理论研究中占有非常重要的地位。
然而,Leipus 等人给出的充要条件并不全面[17],有些条件验证起来也不方便。因此本文继续拟寻找卷积等价分布族关于卷积封闭的其他充要条件。众所周知,次指数分布族是卷积等价分布族的特例,而次指数分布族关于卷积运算的封闭性已有较成熟的结果。如文献[18]给出次指数分布族也不满足卷积封闭性,FOSS S 等人[18]给出关于卷积封闭的若干充要条件,GELUK J 等人给出在最值运算下的封闭性[19]。因此,受次指数分布族关于卷积运算封闭性的启发,本文首先给出卷积等价分布族关于卷积封闭的若干充要条件。在此基础上,设X,Y是两个相互独立的实值随机变量,分别给出了max(X,Y)关于卷积等价分布族封闭的充要条件以及min(X,Y)关于卷积等价分布族封闭的充分条件,拓展了卷积等价分布族研究的理论成果。
本文以下若无特殊申明,均假设X,Y为两个实值随机变量,分布函数分别为F(x)=P(X≤x),G(y)=P(Y)≤y。记其尾分布为。且下文所有的极限过程均指x→∞。对于任意两个正函数f(·)与g(·)满足

若b=0,记作f(·)=o(g(·));若a=b=1,记作f(·)~g(·);若b<∞,记 作f(·)=O(g(·))。下文中I(A)={1or0,A 发生或不发生},记X∨Y=max(X,Y),X∧Y=max(X,Y)。
定义1称分布F属于卷积等价分布族,L(γ)(γ≥0)记作F∈L(γ),若对任意固定y≥0,

定义2称分布F属于卷积等价分布族S(γ)(γ≥0),记作F∈S(γ),如果

其中F2*表示分布函数F关于自身的二重卷积。
注对两个定义做以下说明:
首先,S(γ)⊂L(γ)。其次,当时γ=0,定义1中的分布是长尾分布族,即L(0),且(1)式对y的紧区间一致成立。而此时定义2 中的分布就是次指数分布族,即S(0)。最后,当γ>0 时,由定义2易知L(γ)和S(γ)均是轻尾分布族,但是当γ=0 时对应的长尾分布族和次指数分布族均是重尾分布族,由此可见γ决定了两个定义中的分布族的不同尾性质。
2 引理
引理1若F∈L(γ)(γ≥0),则存在函数h(·):[0,∞)↦[0,∞),满足
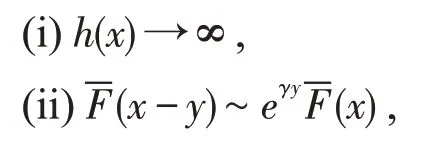
且(ii)对|y|≤h(x)一致成立,此即

进而,如果h1(x)∈H(F),h2(x)≤h1(x),x∈[0,∞),h2(x)→∞,则h2(x)∈H(F)。
证明由注知,当F∈L(γ)时,(1)式对y的紧区间一致成立。故对任意的对|y|≤h(x)一致成立。此即
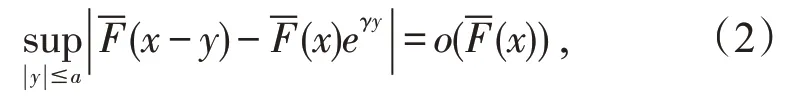
故当a=1,ξ=1 时,存在x1,对任意x>x1满足

依次类推,当a=n,ξ=时,存在xn,且xn>xn-1,对任意x>xn满足

如此下去,找到了一列递增的序列{xn},易见n→∞时,xn→∞。故定义
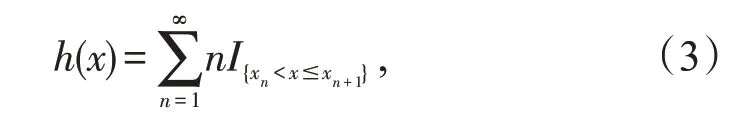
由(3)式容易验证函数h(·),满足条件(i)。而对任意的x,必存在n,使得x∈(xn,xn+1],又因函数h(x)非降,易有h(x)≤h(xn+1)。故

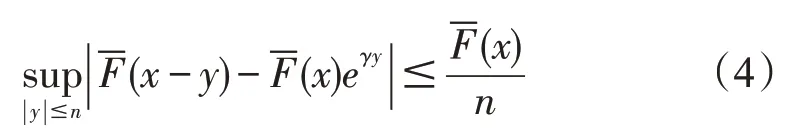
结合(2)和(4)式证明了条件(ii)成立。证毕。
引理2若G∈L(γ)(γ≥0),则对任意满足<∞的分布F以及任意的函数h(x)∈H(G),有

证明因 为G∈L(γ),则对任意的函数h(x)∈H(G),简单计算可得

先处理I1,由于关于y递增,故有下式成立
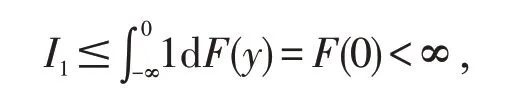
最后处理I2,又由引理1 知对|y|≤h(x)一致成立,故整体可用控制收敛定理得到下式

证毕。
引理 3[20]F∈S(γ)(γ≥0)的充要条件为F+∈S(γ),其中F+为X∨0的分布函数。
引理 4[17]对于任意分布F,若<∞(γ≥0),则F∈S(γ)当且仅当F∈L(γ),
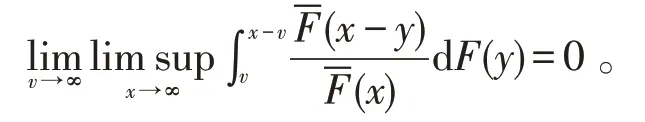
引理5[17]若F,G∈L(γ)(γ≥0),那么下列叙述定义是等价的:
(i)F*G∈S(γ),
(ii)FG∈S(γ),
(iii)对任意p∈(0,1),pF+(1-p)G∈S(γ),
(iv)存在p∈(0,1),pF+(1-p)G∈S(γ)。
且上面的任意一种叙述都可推出
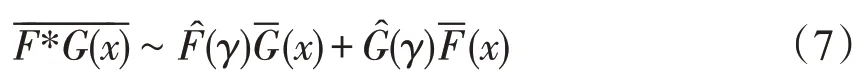
以下记F*G为分布F,G的卷积分布。
引理6[17]若F,G∈S(γ)(γ≥0),则引理5的(i)到(iv)和(7)式等价。
3 主要结果及其证明
定理1若F,G∈S(γ)(γ≥0),那么下列说法是等价的:
(i)F*G∈S(γ),
(ii)FG∈S(γ),
(iv)对任意p∈(0,1),pF+(1+p)G∈S(γ),
(v)存在p∈(0,1),pF+(1-p)G∈S(γ),
(iv)对任意函数h(x),满足当x→∞时,h(x)→∞,则
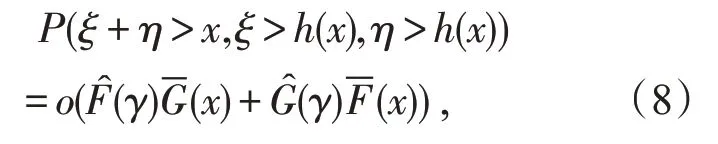
(vii)存在函数h(x),满足当x→∞时,h(x)→∞,则
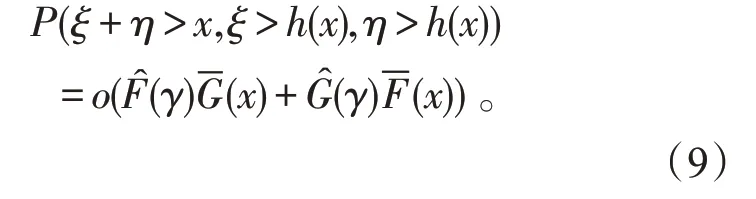
其中ξ,η是两个相互独立的实值随机变量,分布分别为F,G。
证明(i)到(v)的等价证明可见引理5 和引理6,故下面先证(iii)⇔(vi),进而得到前六个说法等价,最后证明后两个说法的等价,从而完整证明该定理。
如果对任意函数h(x),当x→∞时,h(x)→∞,则

方便起见记
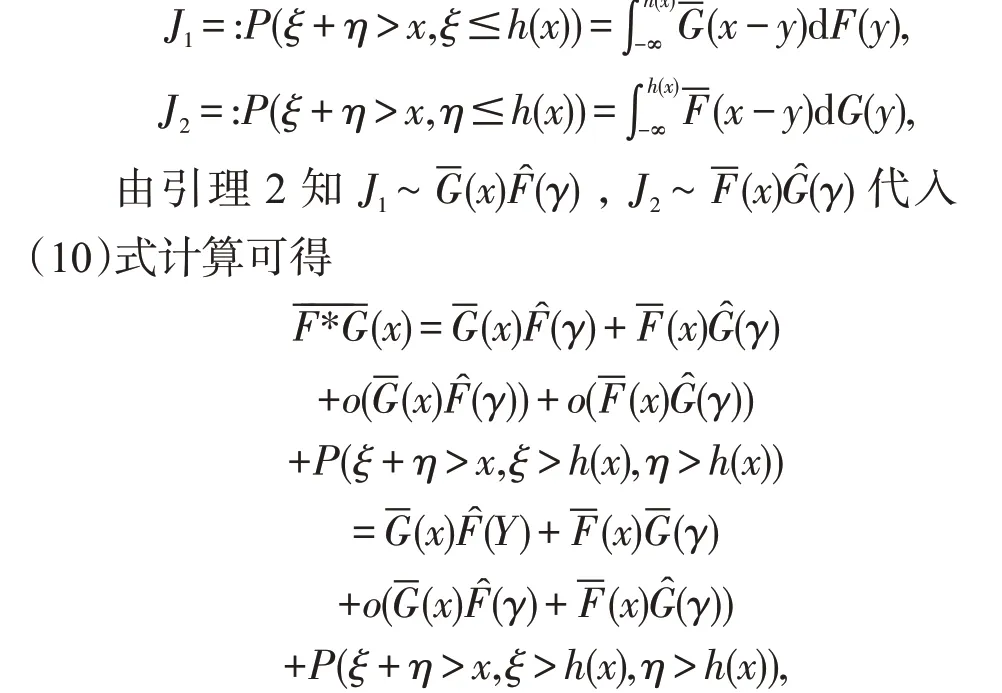
最后的等式成立事实上是因为

综上,若(iii)成立必有(vi)成立,反之亦然,故(iii)⇔(vi)。
下证。显然,另一方面,假设存在函数,由(9)式可有
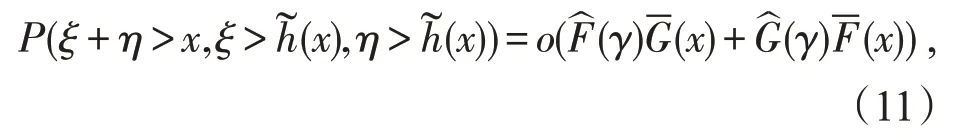
那么对任意h(x)→∞,总会有~h(x) 结合(11)和(12)式可得(8)式成立。证毕。 定理2设X,Y是两个相互独立的实值随机变量,分布分别为F,G。若X,Y∈S(γ)(γ≥0),则X+Y∈S(γ)充要条件为X∨Y∈S(γ)。 证明显然X+Y~F*G,而简单计算可得X∨Y∈FG,故由定理1 知X+Y∈S(γ)充要条件为X∨Y∈S(γ)。证毕。 定理3设X,Y是两个相互独立的实值随机变量,分布分别为F,G。若X∈S(γ1),Y∈S(γ2),(γi≥0,i=1,2)且则X∧Y∈S(γ1+γ2)。 证明首先由引理3可知X∈S(γ)⇔X+∈S(γ),所以不失一般性,以下证明均对非负随机变量讨论。 由引理4知要证H∈S(γ1+γ2),则只需证H∈L(γ1+γ2)以及 注意到 故对任意固定的y≥0,由(14)式简单计算可得 即证H∈L(γ1+γ2)。 而又有 必存在常数c>0,使得对任意x>0 有 事实上,设Y1,Y2是两个相互独立同分布的实值随机变量,且 服从分布G∈S(γ1),则对任意y∈(0,x)有 故可找到常数c>0,(16)式对y∈(0,x)一致成立,进而 又因F∈S(γ1),可根据引理4 有 同理讨论I2(x,v),再结合(17)和(18)式可得 综上由(19)和(13),即证H∈S(γ1+γ2)。证毕。 本文首先得到卷积等价分布族关于卷积封闭的若干充要条件。最后总结了最值关于卷积等价分布族封闭的条件。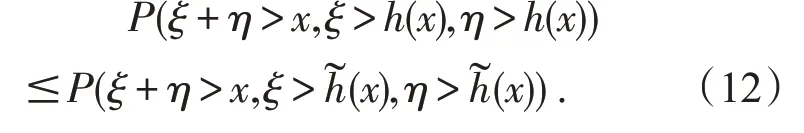
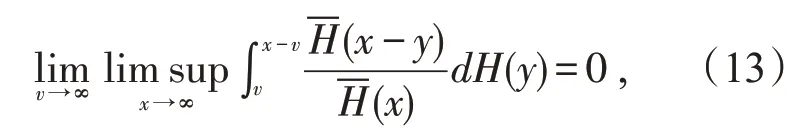
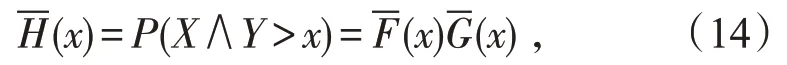
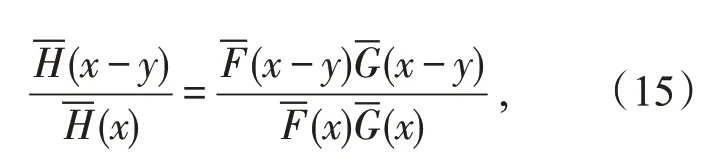
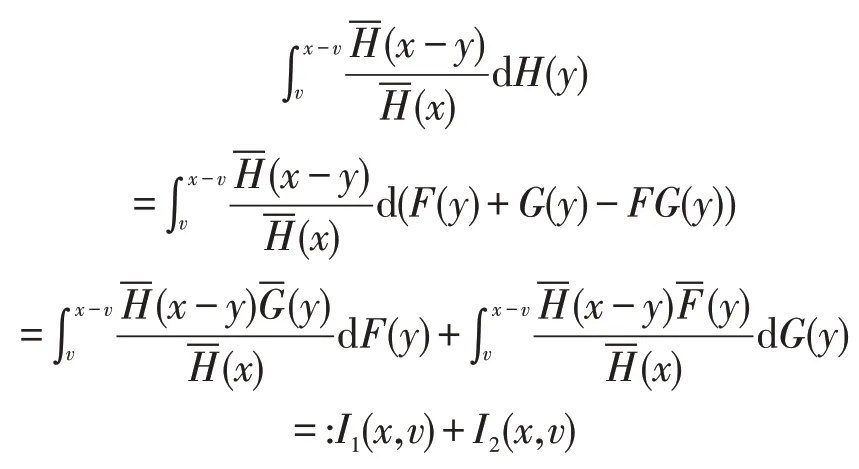

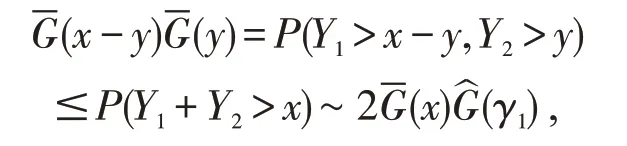

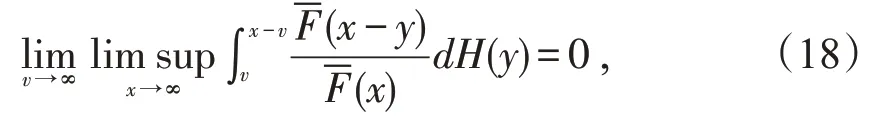
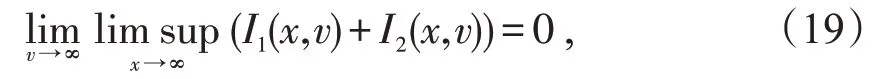
小结

