一类奇异扰动问题解的零点集的几何性质
黄婷薇,张 闪
(1.四川工商学院 计算机学院,四川 成都 611745;2.南京财经大学 应用数学学院,江苏 南京 210023)
生态数学中,如下的非线性椭圆方程组

常被用来描述固定区域中处于竞争状态种群的动力学行为,其中u,v表示竞争种群的密度;Ω ⊆Rn为Rn中具光滑边界的有界区域;函数f,g表示种群的自然增长率;k为描述种群间竞争强度的一个正参数。
1994 年,Dancer 和Du 研究了k→∞时,方程组(1)解的渐近行为[1],证明了系统(1)的解(uk,vk)在H1弱意义下收敛到向量值函数()u,v,且对于a.e.x∈Ω,u,v=0。这就表明奇异极限u,v在Ω 中的支集相互分离。注意到奇异极限的零点集

是一个自由边界。因为和是未知函数,Γ(u,v)预先不确定,随着解的变化而改变。
此后这一相分离现象,被众多的学者所关注。Conti,Terracini 和Verzini[2],Caffarelli,Kara-Khanyan 和Lin[3],Tavares 和Terracini[4]研究了多种群竞争系统在强竞争下解的渐近行为,证明了解关于竞争参数的一致界估计,奇异极限的Lipschitz 正则性以及自由边界的正则性。Dancer,Wang 和Zhang[5,6,7]将上述结果推广到了相应的抛物情形。
在系统(1)以及前面提到的文献中,总假定种群所处的环境是均匀的,且种群的扩散是生物学意义上的随机游走。然而,当种群处于某个特定的非均质环境中,种群不能完全忽视周围的环境。事实上,种群会感知所处环境,诸如气候,食物和捕食者等。它们会通过趋向性运动迁徙到较为适宜的生存环境。换句话说,种群的扩散由是随机游走和有趋向的迁徙两部分构成。为了研究趋向运动对种群空间行为的影响,文献[8]考虑了如下的反应扩散对流方程组:
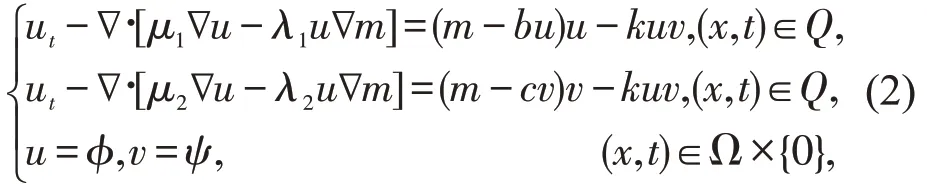
其中常数b,c>0,Q=Ω×(0,+∞),m=m(x)为种群在x处的局部增长率。在某种意义上,m(x)能够反映出空间位置x处资源的性质。一般来说区域{x∈Ω:m(x)>0}表示优势资源区域,而表示资源匮乏区域[8]。μ1和μ2为随机扩散系数,λ1u∇m和λ2v∇m为对流项,非负常数λ1和λ2衡量了两个物种沿着m(x)梯度方向运动的趋势。另外t>0 时我们一般加上齐次的Dirichlet 或者Neumann 边值条件(从而对初值也要求相应的相容性条件)。
文献[9]研究了k→∞时,方程组(2)解的渐近行为。他们证明了系统解关于竞争参数的一致界估计,并证明了奇异极限的支集相互分离。即对于方程组(2)的一列非负解{(uk,vk)},存在函数(u,v)∈Ca(Q)(0 本文将在这一工作的基础上继续研究若干未解决的问题。考虑如下M≥3 个物种竞争的稳态模型: 其中ai≥0,i=1,2,…M;为给定的已知函数。我们用表示(3)的非负古典解,那么利用文献[2]中的blow-up 方法,可以证明方程组(3)解关于参数k的一致界估计[9]。因此,存在U=(u1,u2,…,uM)∈(Ca(Ω))M,使得在子列意义下, 本文将进一步导出奇异极限U满足的方程,并刻画零点集Γ(U)={(x)∈Ω|U(x)=0}的相关性质,从而将文献[4]的结果推广到带对流项的情形。最后,需要说明的是,相分离问题的研究不仅可以对竞争种群的空间行为做出科学的解释,也有助于理解凝聚态物理中Bose-Einstein 凝聚态的相位分离现象,参见文献[10-12]等。近年来,众多学者对相分离问题的研究进行了推广,参见文献[13,14]等。 为进一步研究奇异极限U=(u1,u2,…,uM)的性质,并导出奇异极限满足的方程,需要建立如下强收敛结果。 引理1若{Uk} 是(3)的一列非负解,那么存在使得: (ii)在Ω 中,uiuj≡0,∀i≠j。 证明引理1的证明将分为以下几步。 第一步:存在与k无关的常数C>0,使得 第二步:存在与k无关的常数C>0,使得 考虑如下辅助问题 这样就完成了(5)式的证明。 第三步:存在与k无关的常数C>0,使得 由(4)我们知存在{Uk}的子列,不妨仍记为{Uk},使得 且由(9)以及{Uk}的一致有界性可知,在Ω 中 这样我们就完成了引理中(ii)的证明。 只需证明i=1的情形,其他情况可类似证明。事实上,对的方程两边同时乘以极限u1(i≠j),并在Ω 上积分可得 由(10)式可知 ∇ui∙∇uj=0,ui∙∇uj=0,∀i≠j。 这就使得 注意到由(12) 那么对(13)式取极限可得 取极限 定理1令U=(u1,u2,…,uM)是引理1 中的奇异极限,那么在弱意义下,U满足下面微分不等式: 证明首先注意到, 进一步地,直接计算可得 取检验函数φ∈,分别对(14)与(15)两边乘以φ并在Ω 上积分可得 接下来由引理1 中的收敛性,可以对上面两个不等式取极限,得到在弱意义下,奇异极限U满足 定理1 证毕。 在前一节的基础上,我们进一步刻画零点集Γ(U)={x∈Ω|U(x)=0}的几何性质。 定理2假定U=(u1,u2,…,uM)为方程组(3)的奇异极限,那么存在Γ(U)的相对开集∑(U)使得: (i)Hdim(Γ(U))≤n-1; (ii)任意的0 (iii)Hdim(Γ(U))∑(U)≤n-2,且 特别地,当n=2 时,Γ(U)∑(U)为局部有限点集。 证明为了简化记号,假定λ1=λ2=…λM=1.构造非线性变换: 那么由引理1 知 且类似于定理1的证明,W=(w1,w2,…,wM)在弱意义满足如下的微分不等式 Γ(W)={x∈Ω|W(x)=0}, 那么由W的定义,Γ(U)=Γ(W)。注意到fi(x,0)=0,由(18)式以及文[14]中的推论8.5 知,Hdim(Γ(U))=Hdim(Γ(W))≤n-1;进一步地,存在Γ(W)中的相对开集的相对开集∑(W) 使得Hdim(Γ(W)∑(W))≤n-2;且任意的0 以及∀x0∈Γ(U)∑(U), 特别地,当n=2 时,Γ(W)∑(W)为局部有限点集。 令∑(U):=∑(W),为了完成定理2的证明,仅需证明(16) 与(17) 式成立。注意到∇wi=∇(e-m/2ui)=ui∇e-m/2+e-m/2∇ui,那么 本文研究了一类来源于非均质环境中描述种群竞争的反应扩散对流方程组解的渐近性质,证明了在竞争参数趋于正无穷的奇异极限中,各物种在空间上相互分离并且它们满足一个奇特的微分不等式系统;并在此基础上,刻画了奇异极限零点集的几何性质。本文的工作是对文献[9]的进一步延伸与拓展,同时也将文献[3,4]的主要结果推广到了带对流项的情形。

1 奇异极限问题
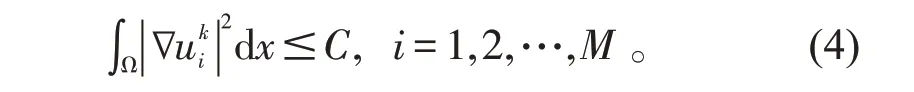
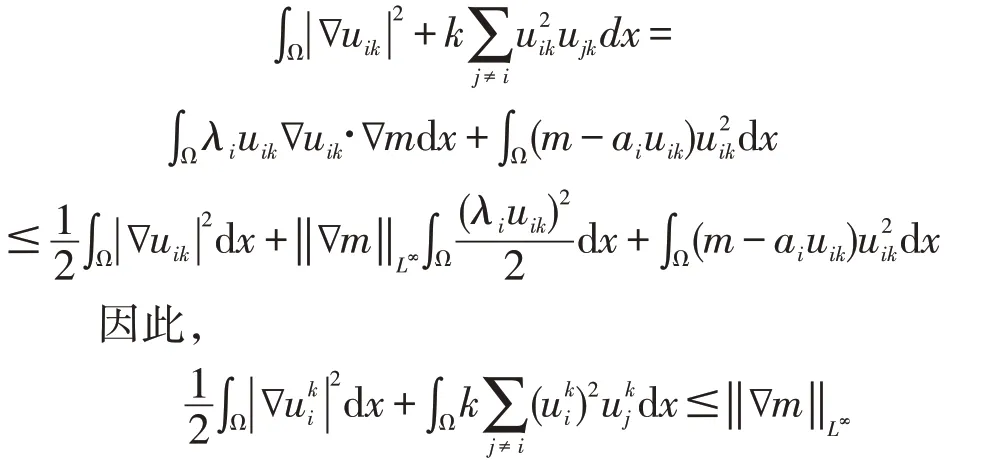
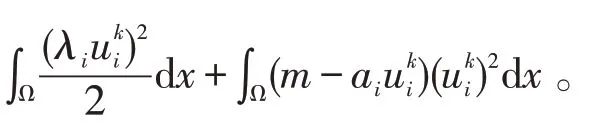








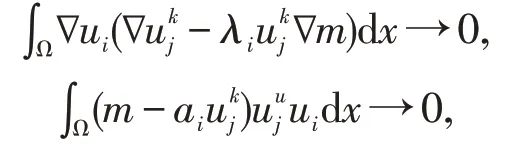


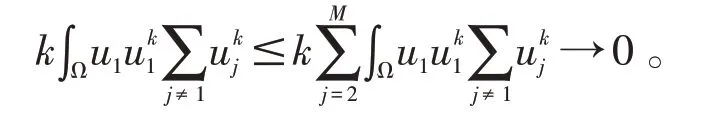







2 零点集的几何性质








3 小结

