随机Cohen-Grossberg 神经网络的有限时间稳定性
孙云霞
(阜阳师范大学 数学与统计学院,安徽 阜阳 236037)
1 引言
过去一段时间,关于Cohen-Grossberg 神经网络[1](简称CGNNs)的研究众多,一些实际系统不可避免地受到时间滞后[2-3],噪声[4-5]和脉冲扰动[6-7]以及系统结构随机改变[8-10]的影响,这可能引起系统的振荡和不稳定性。因此,在CGNNs 系统中必须考虑这几种因素对系统稳定的影响。值得注意的是,现有的大多数文献主要研究了脉冲随机CGNNs的Lyapunov 稳定性。Lyapunov 稳定性通常通过在无限时间间隔内应用控制动力学的稳态行为来处理系统轨迹的渐近模式。而有限时间稳定性常应用于通讯网络系统,导弹系统和机器人控制系统等实际系统的瞬态性能,具有很好的实际意义。目前,一些文献已经研究了随机系统的有限时间稳定性[11-14]。但是,上述文献中考虑受几种因素同时影响的研究却不多,本文在具有Markov 跳和时滞的前提下,考虑了两种不同的脉冲,通过重构Lyapunov-Krasovskii 泛函,研究了脉冲强度和脉冲间隔对随机CGNNs 有限时间稳定性的影响。
2 准备知识
考虑带有Markov 跳和时滞的脉冲随机CGNNs
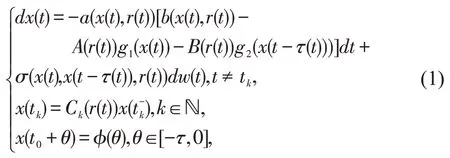
对t≥0,其中,x(t)=[x1(t),x2(x),…,xn(t)]T为神经元状态向量,a(x(t),r(t))=diag(a1(x1(t),r(t)),a2(x2(t),r(t))…,an(xn(t),r(t)))为神经元放大函数,b(x(t))=[b1(x1(t)),…,bn(xn(t))]T为神经元行为函数,矩阵A(r(t)),B(r(t))分别表示为连接权矩阵和时滞连接权矩阵,gj(x(t))=[gj1(x1(t)),gj2(x2(t))…,gjn(xn(t))]T(j=1,2) 为 神经元激活函数,噪声扰动σ:ℝn×ℝn×S→ℝn×m为Borel可测函数。时滞τ(t)满足0≤τ(t)≤τ,≤δ,其中,τ,δ为 常数,w(t)=(w1(t),w2(t),…wn(t))为定义于该空间上的m维标准布朗运动。中的Ck表示为脉冲增益矩阵。而tk满足0 ≤t0 令r(t),t≥0 为定义在概率空间上取值于有限状态空间S={1,2,…,N}的右连续Markov 链,满足P{r(t+Δ)=j|r(t)=i}=其中,Δ>0,o(Δ),为无穷小量,γii=表示从i到j的转移概率。记Γ=(γij)N×N,Γ 是一个N×N的常数转移矩阵。 为了简便,记r(t)=i,i∈S,本文中总假设以下条件成立。 假设1存在正常数,使得:,∀x∈ℝ,l=1,2,…,n。 假设 2存在正常数βil,使得:,∀x∈ℝ,l=1,2,…,n。 假设 3 存在对角矩阵Gj,使得:|gj(x)|≤|Gj·x|,∀x∈ℝ,j=1,2。 假设4 存在对称正定矩阵Mil,Mi2,使得: 设x(t,φ)表示从初始数据x(t0+θ)=φ(θ)∈得到的状态轨迹。由g1(0)=0,g2(0)=0,σ(0,0,i)=0知系统(1)有平凡解x(t,0)≡0。为了简便,记x(t,φ)=x(t)。 定义1[15]若对于给定正常数c1,c2,T,c1 则称系统(1)关于(c1,c2,T)有限时间稳定。 定理1对于系统(1),若存在正常数,α,μ≥1,对称正定矩阵Pi,Q及正定对角矩阵Q1,Q2使得以下不等式成立: 其中: 则称系统(1)关于(c1,c2,T)有限时间稳定 证定义Lyapunov-Krasovskii 泛函 系统(1)轨迹上的Kolmogorov算子为 其中, 由式(2)可得 对式(8)两边从tk到t积分再取期望,结合Gronwall 不等式得 根据文献[16]中的引理3.1,结合不等式(3)推导出 由式(10),对式(9)进行迭代运算可以得到 由文献[17]中的定义2 和式(5-6)可得 另一方面,通过式(5)可得 因此,由定义1 知,则称系统(1)关于(c1,c2,T)有限时间稳定。证毕。 注1:在文中,时滞τ(t)导数的上限δ考虑了δ≤1、δ>1 两种情形,而文献[18,19]中导数上限仅研究一种情形(<1)。因此,本文的结果可以应用于更一般的系统。 定理2对于系统(1),若存在正常数,v,α,μ<1,对称正定矩阵Pi,Q及正定对角矩阵Q1,Q2使得以下不等式成立: 其中:Ω11,Ω22如定理1 所示。 则系统(1)关于(c1,c2,T)有限时间稳定。 证定义Lyapunov-Krasovskii 泛函如(7)所示,由不等式(13),根据定理1 证明的方法可得式(8-9)成立。 根据文献[16]中的引理3.2,通过不等式(14-15)推导出 结合式(20),对式(9)进行迭代运算可以得到 结合式(16,21)可得 由式(18-19,22)推出 根据式(18,23)可得 因此,由定义1 知,系统(1)关于(c1,c2,T)有限时间稳定。证毕。 注2:值得注意的是,在文献[20]中,作者也研究了随机CGNNs的有限时间稳定性。但是,作者没有考虑系统受脉冲扰动的影响。因此,本文的研究更接近于实际的情形。 推论1对于系统(1),若存在正常数,v,α,μ<1,对称正定矩阵Pi,Q及正定对角矩阵Q1,Q2使得不等式(13-16,18)及以下不等式成立: 则系统(1)关于(c1,c2,T)有限时间稳定。 考虑系统(1),其中 令α=0.2,μ=1.1,c1=0.1,c2=10,T=1,N0=3。利用MATLAB 工具箱求解可得满足线性矩阵不等式(2-6)的可行解: ρ>0.0277,本文设ρ=0.03>0.0277,由定理1 可知,系统(1)关于(0.1,10,1)有限时间稳定。 本文研究了具有Markov 跳和脉冲时滞的随机CGNNs的有限时间稳定性问题,并考虑了μ≥1和μ<1两种脉冲情形,对于每种情形分别获得了有限时间稳定的充分条件。然后通过一个数值例子说明了随机Cohen-Grossberg 神经网络有限时间稳定的判定依据是有效的。
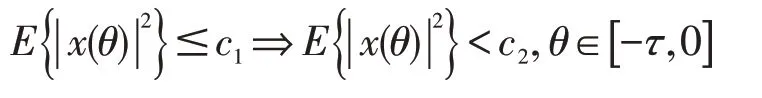
3 主要结果
3.1 不稳定脉冲情形

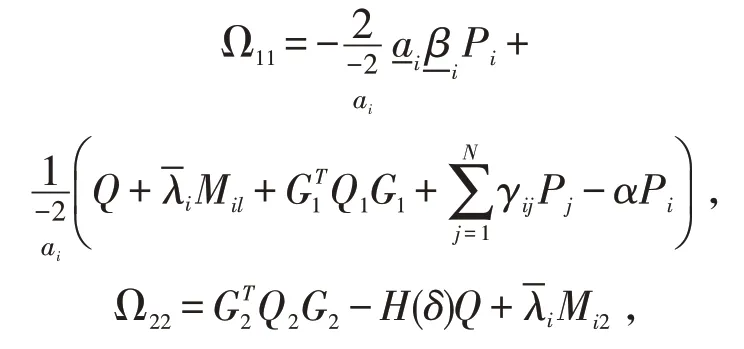





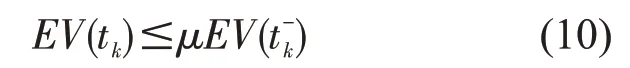


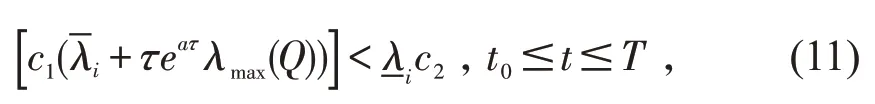

3.2 稳定脉冲情形







4 数值例子



5 结论

