复形的扩张
林 记
(阜阳师范大学 数学与统计学院,安徽 阜阳 236041)
0 引言
同调是拓扑空间的代数刻画。将代数拓扑中的复形、同调群以及边缘等概念引入纯代数的领域,从而形成了代数学中的一个新的研究方向,称之为同调代数。同调与同调函子是同调代数的核心部分。复形是具有分次结构的微分群,是研究同调的有力工具。阿贝尔范畴是一个特殊的正合范畴,从阿贝尔范畴出发我们可以构造复形范畴,这也是阿贝尔范畴。在阿贝尔范畴中,可以通过正合性分析产生各种代数和几何不变量,如同调群和上同调群。扩张的研究源自乘法群的扩张,从形式上看这是一个短正合列。Yoneda 将短正合列通过适当的方式粘合后定义了长正合列,并由此得出了导出函子[1]。扩张是研究同调函子的重要工具[2-4],利用复形的扩张可以证明遗传阿贝尔范畴的有界复形范畴的同调维数是局部有限的[5]。本文主要研究有界复形的扩张的若干性质。
1 有界复形的同调维数
首先回忆本文所需的同调代数的基本概念[1-4]。
设A是阿贝尔范畴,用Cb(A)表示A上的有界复形范畴。
定义1设A∙,C∙∈Cb(A)。若存在复形的长正合列

定义3若两个从A∙到C∙的n阶扩张S与S′之间存在一系列态射
S=S0→S1←S2→…←S2k-2→S2k-1←S2k=S′,且这些态射均具有(1A∙,…,1C∙)的形式,则称S与S′是等价的,记作S≡S′,并将从A∙到C∙的n阶扩张的等价类构成的集合记作
定义4[5]设A∙∈Cb(A)。如果存在整数d,满足对任意C∙∈Cb(A)都有

那么称复形A∙的同调维数不超过d。
设X∈A,m∈ℤ。以下用UX,m表示X位于第m次齐次分支的stalk 复形,KX,m表示如下无环复形

其中X位于第m-1 次和第m次齐次分支,称之为标准无环复形[5-7]。在不引起混淆的情况下,我们也用UX,m和KX,m分别表示它们所在的等价类。
命题5 设A的整体维数有限,那么任意有界无环复形的同调维数有限。
证明设g1.dimA=d。
首先证明对任意X∈A,m∈ℤ 标准无环复形KX,m的同调维数不超过d。对任意M∙∈Cb(A),任取,不妨设[]S是正合列



由此可得复形的正合列




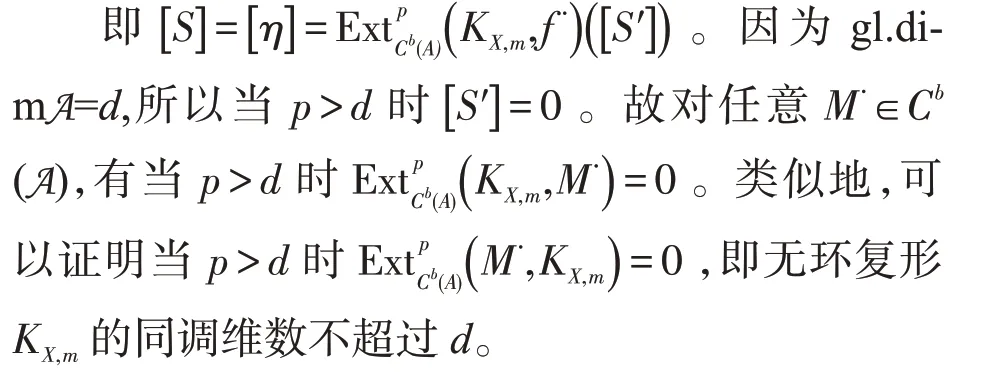
因为任意有界无环复形均可由标准无环复形经过有限次扩张得到[8-9],所以任意有界无环复形的同调维数不超过d。证毕。

那么有复形的链可裂正合列

定理6设A的整体维数有限,那么任意有界复形的同调维数有限。
证明设gl.dimA=d。
因为任意有界复形均可由stalk 复形经过有限次扩张得到,所以我们只需证明stalk 复形的同调维数有限。为此,任取A,B∈A,m,n∈ℤ。


所在的等价类。由复形的左强制截断和右强制截断的性质知,有如下复形正合列间的态射


故对任意p>d,有

其次,不妨设m>n。用函子作用在短正合列


2 零微分复形的扩张
若复形A∙的微分为零,则称之为零微分复形。下面我们讨论零微分复形的扩张的性质。维数向量是范畴理论中重要的概念[11],在Ringel-Hall 代数理论[12-14]、李理论[15-17]和丛代数理论[18-19]中有着重要的作用。沿用文献[11]的记号,用K0(A)表示阿贝尔范畴A的Grothendieck 群,A是阿贝尔范畴A的对象,用表示A在K0(A)中的像,称为A的维数向量。
定理7设A∙,B∙∈Cb(A)是零微分复形,则Cb(A)中的任意扩张
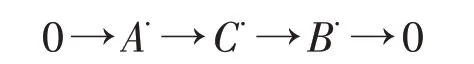

证明由同调代数的基本理论知,对任意i∈ℤ,有下列A中的正合列

因此该线性方程组有唯一解[20],即得结论。证毕。
3.小结
本文利用扩张的性质得到阿贝尔范畴的整体维数与其上有界复形范畴的整体维数的关系,并得到零微分复形的扩张的中间项的微分与其同调的关系。进一步可考虑两个范畴的相关数字特征间的关系,亦可将结论推广至周期复形范畴。

