陈题新得：一道高考试题的变式探究与反思

江苏省锡山高级中学 (214074) 顾晓峰

1 引言

受文[1]的启发，笔者基于2010年高考数学江苏卷第18题第3问开设了一节变式探究课，问题主要考查了解析几何中的一大热点——定点定值，其解决过程蕴含着不同的解法角度，具有纵向延伸，横向推广的探究价值.笔者陈题新探，精心设计，采用过程性变式[2]的方法引导学生对问题从不同角度、不同层次进行探究，取得了良好的效果.

2 变式探究的过程

2.1 起：起于考题，初探解法

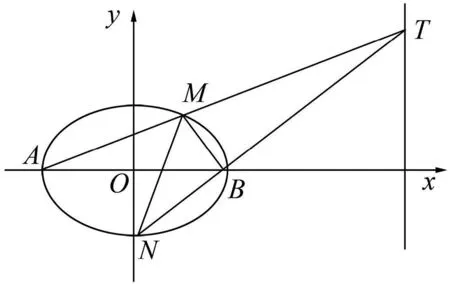
图1

对于此问题，学生的主流思路是通过联立方程及韦达定理用m表示出M、N的坐标，再试图表示出MN的方程研究.笔者提醒注意的斜率是否一定存在，于是优化了做法，先讨论斜率不存在的情况猜出定点，再对一般情况加以证明(利用三点共线)，这样处理相对便利些.

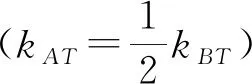
2.2 承：承接思路，逆向探寻

2.3 转：转变眼光，纵深变式

结论3和4的条件中的要素有左、右顶点和直线x=m(或定点(n,0))，那能否将条件适当改变得出类似结论呢？笔者组织学生分组合作探究，并选取两组同学分享成果.

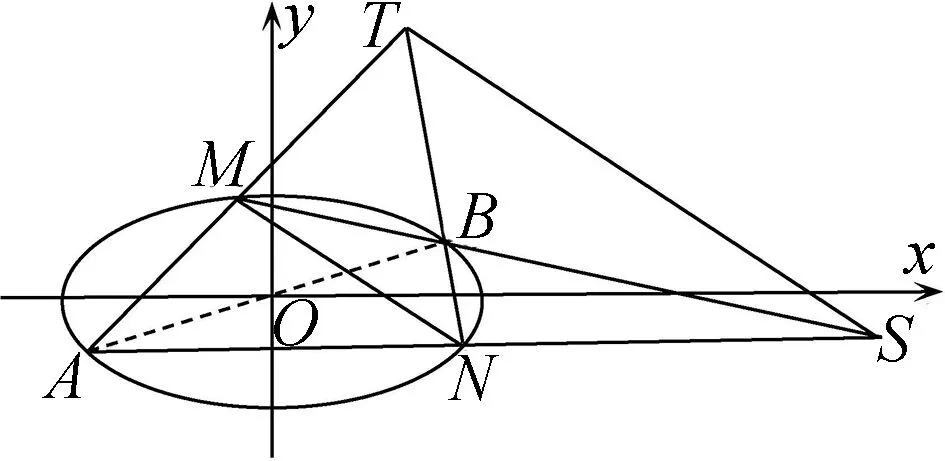
图2

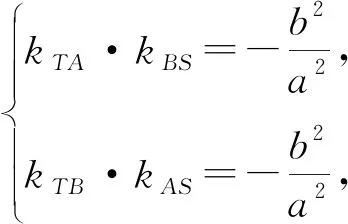
2.4 换：换类思考，扩展成果

课堂的最后，笔者和学生总结了今天的收获(7个结论)，同时抛出思考：这些性质在椭圆上成立，那在其它类型的二次曲线上会成立吗？双曲线与椭圆有着诸多相似之处，故类比方法，请学生课后尝试在双曲线上探究结论3、4、7，作为课后作业.

最终整理学生的探索成果如下：

3 变式探究的思考

3.1 变式探究利于数学抽象素养的发展

数学抽象是表现在获得知识规则、形成思想方法、认识结构体系的重要核心素养.变式探究的教学起点可以是单一化的问题，但通过变化问题条件和结论，一般化问题，转变模型等方式，引发学生对起始问题不断探索进而抽象出新的知识或方法，透过现象看到问题本质从而不断完善自身认识结构，这种低开高走而后又高瞻远瞩的教学模式利于培养学生的数学抽象素养.

3.2 变式探究应当遵循学生的认知规律

有想法才能有做法，有做法才能有方法，也就是说在变式探究教学中，起始问题要易于激起想法，教师也要尊重学生的想法.在实践方面笔者分享两点心得：第一，能以考题、教材中的重要结论为依据生成系列化的变式.因为素材的选取既要有针对性，更强调基于学生已有的知识基础，而优质的高考试题或模拟试题具有很好的融合性与延伸性，教材中的部分结论生根于最基础的数学知识却又蕴含着使用的普适性与多样性，两者若能加以整合必是相得益彰的.例如本例的探究反复用到了与斜率乘积为定值有关的重要性质，这实际上是苏教版选修2-1习题2.3(1)第5题衍生的一个结论，其研究价值极广，适合深入挖掘；第二，尊重学生想错了.因为想错了表明存在认知偏差，例如课堂中有学生试图将的位置推广为任意关于原点对称的两点，我们应赞扬学生大胆思考的动机并理解其想法的合理性，同时抓住教学契机，因为纠正错误本身伴随着检验与反思，这利于学生形成批判性思维习惯.此外，有时站在错误的肩膀上若能发现意外的收获，这无疑是令人欣喜的.

3.3 变式探究促使教师提升教研能力

“教而不思则罔，思而不研则殆”，新课标的指向是在数学课堂中落实“四基四能”，那么教师本身应由单纯的解题者转变为在解决问题之下更能发现问题、提出问题的教研者.变式探究促使教师领会命题者背后的心思，结合平时的广泛阅读、研讨与思考，深挖问题内涵，用研究成果来指导教学，最终实现教研相长.