立足“厚”“薄”教学 培养数学抽象素养

江苏省灌南高级中学 (222500) 唐志林 刘鑫钧

《普通高中数学课程标准(2017)》(以下简称《新课标》)最大的一个亮点就是数学核心素养的提出.史宁中教授曾指出新课标所设定的核心素养的本质就是抽象、推理、模型[1]，而数学抽象素养又居于六大核心素养的首位，因此对于如何培养和发展学生的数学抽象素养就显得尤为重要.然而在高三复习教学中学生往往只见“厚”的教学，却未见教学的“薄”，因此需要提高学生对问题不断抽象的水平，从而把握问题本质.本文拟就在“厚”“薄”数学观下研究如何培养学生的数学抽象素养.

一、“厚”“薄”数学观与数学抽象素养

(一)“厚”“薄”数学观

道生一，一生二，二生三，三生万物，学习的关键在于领悟到“道”，而要领悟到“道”就需先得“一”，这个“一”应该是简单的，也是最本质的.在平常的教学中，我们总是追求结论清晰，尽量做到一言以蔽之，就是对“薄”的追求.同时我们也总是希望解法简洁明了，让学生一看就能明白问题的本质，亦是对“薄”的苛求.因此，“薄”就是简单、简洁、简约，就是老子所讲的“一”，是我们在数学教学中的最高追求.然而在高三复习教学中学生往往被厚厚的书本和沉甸甸的试卷压得喘不过气来，教师不断的重复拉网式的讲题，使学生不堪忍受.因此，“厚”体现在多杂、繁杂、乱杂，就是老师所讲的“万物”.平常教学中的“厚”使得学生陷入题海而不能自拔，使得学生只见“万物”而未得“一”.

(二)数学抽象素养

所谓抽象，是指从一类事物中舍去个别的、非本质的属性，抽取共同的、本质的属性的思维过程.抽象的本质是对同类事物的刻画与构造.数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的过程.主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征.数学抽象具有纯粹性、层次性、形式化等特征.

一是纯粹性.数学抽象只考虑数量关系与空间形式，譬如我们只见过直的木棍，直的铅笔，但是谁又曾见过数学研究对象中真正的“直线”.经数学抽象所得到的概念、命题等是属于“理性的世界”.譬如，用笔画出了圆，圆画好了，但这真的是圆吗？事实上线条上的每个点一定不会跟圆心有相同的距离，因此是个不完美的圆，而数学定义上的圆，线条不能有宽度，线条上的点到圆心的距离都是相等的.真正的圆是不可画，也不可见，只能通过思想认知，圆是作为一个理性来认知，因而数学抽象具有纯粹性.

二是层次性.对于有感性的、现实的事物或问题上升为数学抽象，往往需要经历多个层次，即可以进行多级抽象.从现实中的距离感抽象出欧式几何中的距离，再逐级抽象到泛函分析中距离的概念：X是任意一非空集合，对于X中任意三点x,y,z，存在一实数d(x,y)满足d(x,y)≥0，当且仅当x=y时取等号；d(x,y)=d(y,x)；d(x,y)≤d(x,z)+d(z,y)，则称d(x,y)为x与y之间的距离.正如徐利治教授所说：数学抽象概念的发展是具有层次性的.抽象层次越高，概括性亦越强,其应用就更具广泛性.

三是形式化.数学符号是数学思维的重要载体，大量数学符号的使用，才使得对数学对象的研究转为形式化的分析变得可能，使得数学概念、命题及公式等在表述上更加简洁、严谨，在思维上更加清晰、有序，在理解上更容易认识本质结构及内在联系.

二、“厚”“薄”数学观下数学抽象素养培养的策略

我们认为，应该从展“形”、变“形”与析“形”，忘“形”，得“一”这五个过程来阐述在高三复习教学中如何忘“形”得“一”，实现教学的“厚”向教学的“薄”的转化.

(一)展“形”——表征图形中元素位置形态

《普通高中数学课程标准》(2017)强调：对学生“直观想象”这一数学核心素养的培养，指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，培养理解和解决数学问题的素养.因此，在解题教学中要鼓励学生把试题中元素的位置形态用图形语言表示出来.从哪入手呢？

例过点P(-4,0)的直线l与圆C:(x-1)2+y2=5相交于A，B两点，若点A恰好是线段PB的中点，则直线l的方程为.

例题的图形表征大致如图1所示，在表征的过程中认识到只有当l处于一个特定位置的时候，A才可能恰好是线段PB的中点，在画图的过程中，发现学生画图的顺序有所不同，有的同学是先画直线，后标注点A，B，即先产生直线，因此可以先假设直线斜率k，然后求点；也有同学先画点，再连接两点所在直线，最后出现另一点，这样就可以设点来做.利用几何图形描述问题，借助几何直观理解问题，在图形表征过程中实现了动态的理解问题.

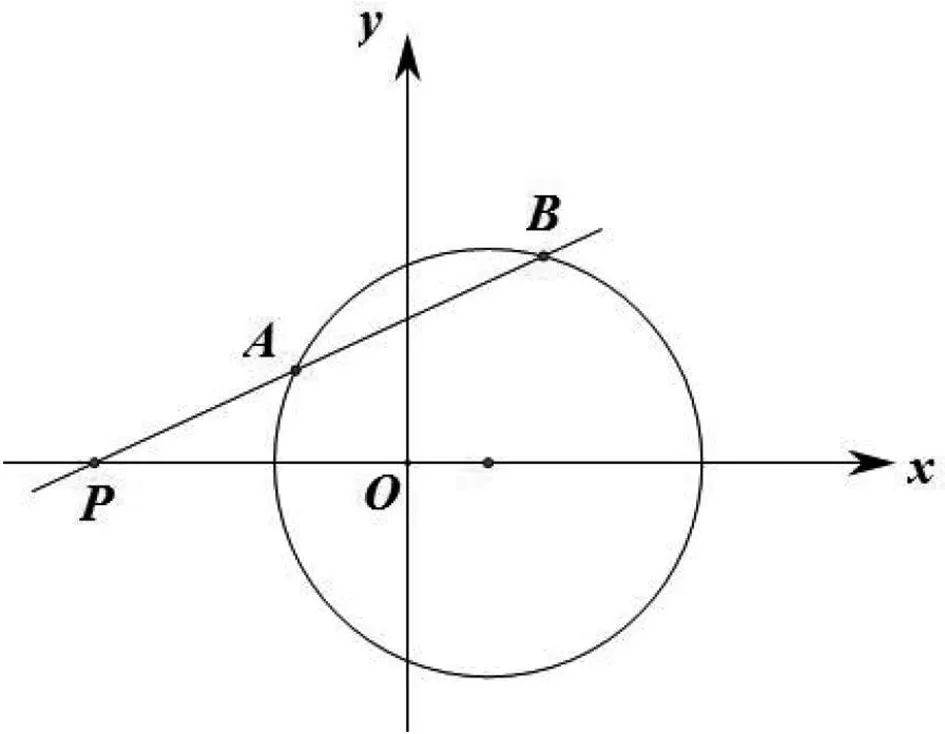
图1

(二)变“形”——变换图形中元素及位置关系

解题教学不仅要一题多解，更要善于多题归一，要善于对问题进行变式，通过变式教学，使数学教学有层次地递进，从而深化对这类问题本质的认识.

1.改变元素

①由定点变动点得到：

变式1 过点E(2,t)作直线l与圆C:x2+y2=1交于M，N两点，若M点恰好是线段NE的中点，则实数t的取值范围是.

②由竖线变斜线得到：

变式2 已知圆C:(x-2)2+y2=1，点P在直线l:x+y+1=0上，若过点P存在直线m与圆C交于A，B两点，且点A为PB的中点，则点P横坐标x0的取值范围是.

③由定圆变动圆得到：

变式3 已知△ABC的三个顶点A(-1,0)，B(1,0)，C(3,2)，其外接圆为⊙H．对于线段BH上的任意一点P，若在以C为圆心的圆上都存在不同的两点M,N，使得点M是线段PN的中点，求⊙C的半径r的取值范围.

2.变更条件

①由中点变向量得到：

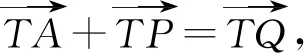
图2

②由直线变动圆，中点变比例得到：

变式5 在平面直角坐标系xOy中，圆C1:(x+1)2+(y-6)2=25，圆C2:(x-17)2+(y-30)2=r2．若圆C2上存在一点P，使得过点P可作一条射线与圆C1依次交于点A,B，满足PA=2AB，则半径r的取值范围是.

(三)析“形”——整合相关图形

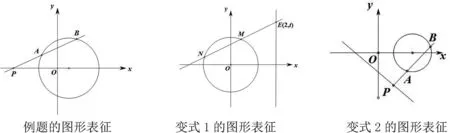
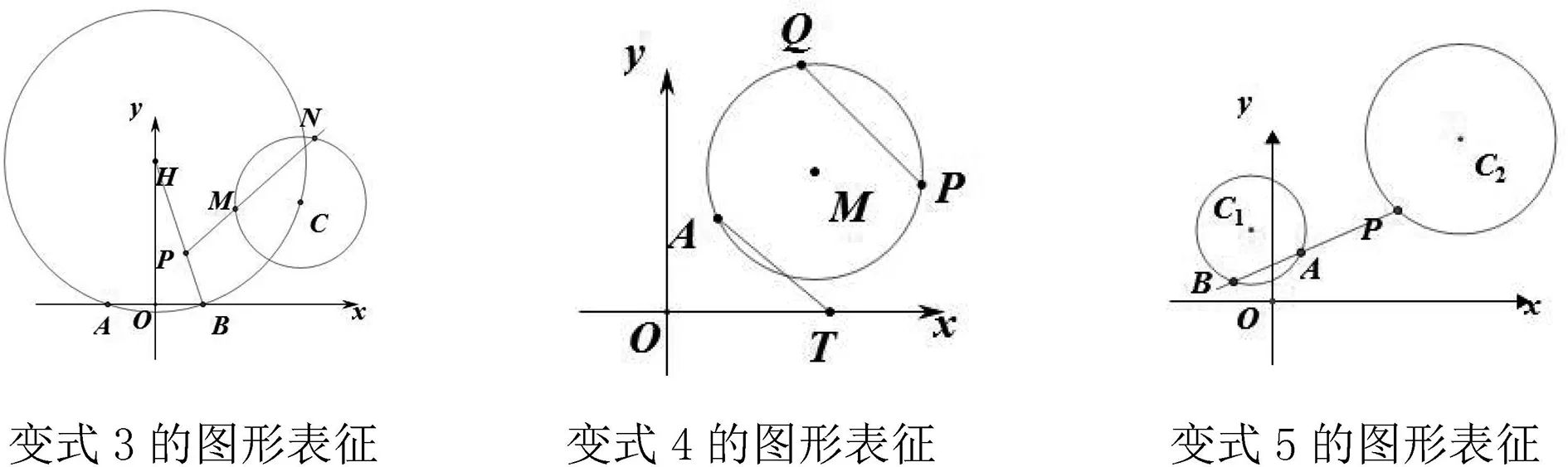
例题及相关5个变式的图形表征如上图所示，下面需要的就是整合这六个图形，即把一些零散的内容通过某种方式而彼此衔接，其主要的精髓在于将零散的要素组合在一起,并最终形成有价值有效率的一个整体.

(四)忘“形”——抽象基本模型

首先，我们可以看出例1至变式2，定点变动点，直线可以是横线(x轴)亦或是竖线与斜线，其中线段比例关系为1∶1，圆始终是定圆.因此，这三个图形可以抽象为下列一个基本的模型.

模型一过直线l上一点P作一条直线，交定圆于A，B，其中PA∶AB=1∶1.

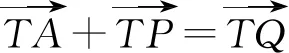
(五)得“一”——对模型本质的概括与普适性解法的提炼

在高三的解题教学之中，如果我们就题讲题，那么教师与学生都将陷于题海之中而不能自拔，如何得其“一”，而忘其形呢？关键的一步就是要对题型及解法抽象，并实现归一.

1.题型的概括抽象

2.解法的提炼与统一

由以上分析我们发现这些试题本质上是一类题型，因此，在教学过程中应引导学生掌握这一类题型的普适性解法，而不是一题一题的讲解.为便于具体说明，这里以曲线C为直线或圆，C1为圆H:(x-a)2+(y-b)2=r2为例.

三、结语

教师在平常的解题教学过程中不仅要让学生获得问题的解决，更应当培养学生对一类问题解决的能力，这就需要对问题不断的展“形”、变“形”、析“形”将知识读厚，通过忘“形”及抽象将知识、方法不断读薄，乃至得“一”，让学生不断经历抽象的过程，培养学生对一类问题模型的识别与概括能力，让学生领悟一类问题解决的具有普适性的思维方法.既要看到树木，更要看到深林.不仅要锻炼学生解决问题的灵活性，更要突出对解法共相、本质上的提炼，从而使数学抽象素养在课堂上真正落地.