从“定义描述”到“逻辑推理”——由“曲线与方程”课堂教学引发的思考

浙江省象山县第二中学 (315731) 马燕青

最近，笔者参加了县教坛新秀的课堂教学评比，课题是“曲线与方程”.“曲线与方程”是解析几何核心思想——“用代数方法研究几何问题”的理论依据，它解释了曲线与方程之间的对应关系，展现了“数与形”、“静止与运动”的对立统一.因此，本节课在高中数学中的教学地位非常重要.

1 教学的目标定位：“学生能够描述定义”

在教材(人教A版)中，本节课只占区区“30余行字”，所有的内容都是围绕着“曲线方程”与“方程曲线”的概念展开，因此，笔者认为本节课的教学目标就是让学生理解什么是“曲线方程”与“方程曲线”的基础上能够对具体的问题进行“纯粹性”与“完备性”的证明.主要教学过程如下：

1.1 创设情境，引入课题

问题1 已知曲线C：第一、三象限角平分线和三个方程f(x,y)=0：①x-y=0,②x-y=0(x≥0),③|x|=|y|，试判断 ：

(1)曲线C上各点的坐标是否都是相应方程f(x,y)=0的解 ；

(2) 以相应f(x,y)=0的解为坐标的点是否都在曲线C上?

意图：直接设问明晰思考方向，适当反问诱发学生的深入思考，为曲线与方程概念的获得铺设第一步台阶.

问题2 你能写出下列图1，图2曲线对应的方程吗？

图1 图2

意图：利用学生熟悉的曲线写出其相应方程，进一步理解曲线上的点的坐标与方程的解之间的对应关系，为曲线与方程概念的获得铺设第二步台阶.

1.2 自主探究，形成概念

问题3 根据上述两个问题的解答，请回答下面两个问题：

(1)对给定的曲线C，如用一个方程f(x,y)=0来表示，那么该方程应该满足哪些条件？

(2)在给定的平面直角坐标系中你认为每条曲线C是否只有唯一的方程f(x,y)=0和它对应？反过来呢?

意图：揭示曲线与方程之间的对应关系，抽象出“曲线的方程与方程的曲线”的概念.

一般地，在给定的平面直角坐标系中，如果某曲线C上的点与一个二元方程的实数解建立了如下的关系：①曲线上的点的坐标都是这个方程的解；②以这个方程的解为坐标的点都是曲线上的点.那么，这个方程叫做曲线的方程；这条曲线叫做方程的曲线.并说明曲线的方程反映的是图形所满足的数量关系;方程的曲线反映的是数量关系所表示的图形.

1.3 数学运用，深化概念

例1 判断下列命题是否正确，并说明理由.

(1)到x轴距离等于1的点的轨迹方程为x=1；

(2)△ABC的顶点A(0,-3),B(1,0),C(-1,0),D为BC的中点，则中线AD的方程为x=0；

(3)到两坐标轴的距离之积等于1的点的轨迹方程为|xy|=1.

例2 证明：以坐标原点为圆心，半径等于2的圆的方程为x2+y2=4.

意图：用两道例题来深化对“曲线与方程”概念的理解，学会用围绕着曲线的方程与方程的曲线的定义来验证数与形之间的等价性.

教学反思：通过本节课的教学，学生基本能够求出曲线对应的方程，但在证明“曲线与方程”的等价性时却出现了问题.学生看似能够熟练的“描述”曲线的方程与方程的曲线的等价性.比如，在例2中，学生会说“圆上点所对应的坐标都是方程x2+y2=4的解，反过来以方程x2+y2=4的解为坐标的点都在圆上”.随后，笔者把问题改为“求以坐标原点为圆心，半径等于2的上半圆的方程”，学生给出的曲线方程是“x2+y2=4(y>0)”，方程显然正确，但当笔者问道“怎么证明所求的方程就是半圆的方程”，学生给出的理由就是把对“例2”描述重复一遍，唯一的差别就是把其中的“圆”替换成了“半圆”，当笔者追问“怎么验证半圆上的点都满足方程x2+y2=4(y>0)” 时，多数学生一脸茫然…，可见，学生是“知其然而不知其所以然”，对“方程与曲线”的一致性的证明只是停留在对概念本身的“描述”阶段，而没有真正的理解其中的数学原理，即为什么可以这样描述？

2 反思：“定义描述”无法替代“逻辑推理”

本节课的教学为什么不能取得预期的教学效果，主要原因是教学难点没有得到真正的突破.表面上看，“曲线的方程与方程的曲线”的概念是本节课的重点与难点，似乎概念能“描述”清楚，教学目标就能够达成，从而导致教师过分地关注对“曲线的方程与方程的曲线”概念本身的描述，而忽视了对“曲线与方程”等价性原理的揭示，其所产生的后果就是学生对“曲线与方程”的认知只能在记忆与模仿的低级思维层面徘徊，面对具体的问题只能是“依样画葫芦”.

实际上，“逻辑推理”才是这节课的核心，从“曲线与方程”概念的生成到判断证明，无一不需要经过逻辑推理.作为数学核心素养之一的逻辑推理，它是一种基于事实和命题，并根据规则推导出其他命题的素养.逻辑推理主要包括两类推理：一类是从特殊到一般的推理，主要有归纳、类比两种推理形式；另一类是从一般到特殊的推理，主要就是演绎推理.在本节课中，一方面，需要通过归纳与类比推理来“验证某个特殊点在或者不在曲线上”从而引导学生发现“曲线与方程”之间的关联性，获得“曲线的方程与方程的曲线”的概念；另一方面，需要通过演绎推理从纯粹性与完备性两个角度来验证“曲线与方程”的等价关系，从而使学生掌握推理的基本形式和规则，体会以形描数，以数叙形，数形一统的解析几何基本思想.但教学中以“定义描述”来替代“逻辑推理”的不当做法淡化了证明的推理属性，导致学生对“曲线与方程”的理解无法触及本质.

3 教学目标再定位：“学生学会逻辑推理”

由此可见，学会逻辑推理才是“曲线与方程”这节课的教学重点.推理作为不可或缺的思想方法，渗透在数学的产生与发展过程中，数学家陈省身说过，学生应该学会推理，推理很要紧， 推理不仅在数学，在其他学问里也是要用到的.《普通高中数学课程标准(实验)》明确指出，培养和提高学生的演绎推理或逻辑证明的能力是高中数学课程的重要目标，合情推理和演绎推理之间联系紧密、相辅相成.由于学生第一次接触关于“曲线与方程”关系的严格论证，缺乏相关的学习经验，因此，需要对推理的过程进行系统的设计.

3.1 立足“运动中的不变性”，明确推理的依据

对于“曲线与方程”等价性的推理主要存在两大障碍：一是“曲线”呈现出来的是直观的“形”，而方程反映的是抽象的“数”，它们分属于不同的数学对象，很难进行直接对比；二是曲线上有无数个点，方程有无数个解，从数量上无法做到逐一对比.突破这两大障碍的关键是要找到沟通“曲线”与“方程”的桥梁.那这个桥梁到底是什么呢？其实就是曲线所遵循的运动规律、几何属性，即“运动中的不变性”.

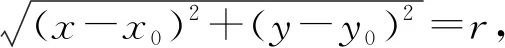
又比如，证明“第一、三象限角平分线”与方程“y-x=0”的等价性，关键要验证曲线上的点与方程的解都满足角平分线的几何属性，即“到角两边的距离相等.“第一、三象限角平分线”上任意一点的坐标为(x,x)，显然到两坐标轴的距离都相等；方程“y-x=0”的任意一组解都满足|y|=|x|，进一步变形为|y-0|=|x-0|，根据绝对值的几何意义，方程所表示的就是“到坐标轴两边距离相等”.不论是“第一、三象限角平分线”，还是方程“y-x=0”，它们都是对角平分线几何属性的刻画，因此它们是等价的.

如图3，在解析几何中，一方面用方程来表示曲线“运动中的不变性”，另一方面可以通过分析方程的结构特征来发掘其所蕴含的“运动中的不变性”，从而实现数形一致性的验证.由此可见，“运动中的不变性”才是“曲线与方程”等价性推理的依据，这个依据教材虽然没有明确指出，但纵观前面的直线与圆，还是后面的圆锥曲线，都是按照“探索定义——求解方程——等价性检验”套路展开的，其中“探索定义”实质上就是研究曲线“运动中的不变性”，只有定义得到明确方程才能得以求解.因此，在本节内容的教学中，首先应该强调曲线上点的“运动中的不变性”，即要把曲线的“定义”凸显出来，在学生明白“曲线是怎么来”的基础上再进行等价性的推理.

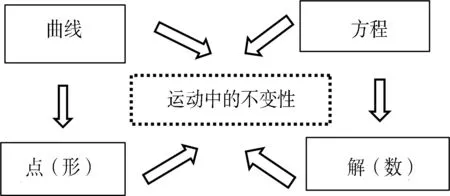
图3

3.2 经历特殊到一般的过程，明确推理的步骤

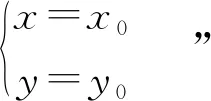
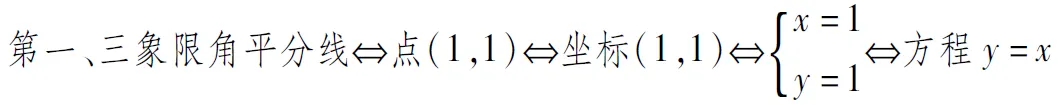
图4

数学概念一般分为两类，一类是对现实对象或关系的直接抽象，这类概念与生活现实接近，容易理解；另一类是纯粹的数学逻辑构造，这类概念高度抽象，没有客观现实与之对应.“曲线与方程”恰恰属于后一类，从浅层上看它是对两个概念的抽象表述，但从深层次上看恰恰是对两个概念逻辑关系的验证.李邦河院士认为 “数学从根本上玩的是概念”，因此，教师要依据数学概念类型来规划教学流程，在教学中更是要做到“不惜时,不惜力”.