多解探究促思维 非主干知识也精彩*——以一道2020年高考向量题为例

福建省莆田第二中学 (351131) 蔡海涛厦门大学附属实验中学 (363123) 林运来

一、试题呈现及分析

试题主要考查平面向量的基本概念、向量的线性运算、平面向量的基本定理及坐标表示、平面向量的数量积等基础知识；考查推理论证、运算求解、创新意识等能力；考查化归与转化思想、特殊与一般思想，考查直观想象、数学运算等核心素养，具有一定的创新性，是一道有显著特色的小题.

二、解法分析

运算求解能力是思维能力和运算技能的结合，是依据运算法则解决数学问题的能力.此题在解答时要求考生学会选择合适的方法(或构造图形求解、或引入向量的坐标求解、或根据向量数量积的定义求解)、合适的运算公式，更重要的是要合理选择运算途径，合理确定运算的方向.

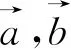
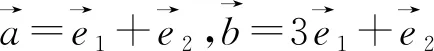
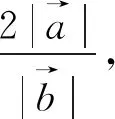
图1

三、解后反思

1.重视非主干知识的复习

非主干板块指的是在整个高中课程内容体系中，由“六大主干”以外的内容组合在一起构成的一个特殊板块(含集合、算法初步、平面向量、不等式、常用逻辑用语、推理与证明、数系的扩充与复数、计数原理等内容).平面向量是高中数学的非主干板块，课时占比相对较少，但在高考试卷中所占分值较大，着重考查平面向量的基本概念、向量的线性运算、平面向量的基本定理及坐标表示、平面向量的数量积、向量的应用.因此，对于本板块内容的处理，应该力求用较少的时间取得较大的分值比例，但是从具有选拔性质的高考答题得分角度来说，每一分都非常重要，尤其是对基础类考题，考生应避免失误而丢分.所以对非主干知识复习备考的关键在于掌握基本概念和基本运算，厘清易错易混概念，领会数学思想方法，把握数学内容的本质.

2.不可忽视的向量工具功能

向量是数学和其他一些学科进行研究的重要且有力的工具，同时也是连接代数与几何的桥梁之一[1].通过向量可以将几何问题和代数问题有机地结合，既可以通过代数运算得到几何不变量和几何量之间的关系，也可以给代数赋予几何直观.向量既有大小，又有方向，是数与形相结合的一个运算量，所以在运算时即可使用“形”的方法进行运算，也可使用“数”的方法进行运算，有时还需借助“数”与“形”相结合的方法进行运算.此题考查了向量的概念、向量的位置关系与模的运算和向量运算的几何意义等知识点，考查的内容源于教材.考生既可以利用向量的几何意义和代数运算求解，也可以通过坐标法求解，解法灵活多样，不同思维能力层次的考生都可以利用自己熟悉的方法来解决问题.

总之，对于一道试题，如果只追求最基本的做法，而忽略其试题本身所含有的基本数学思想、数学方法，其价值就会大打折扣.试题求解，应注重在发挥一题多解背景下的功能与价值，以期达到最小的投入，获得最大的产出，这样日积月累，解题意识与解题能力才会不断提高.