重视从函数的角度认识数列

上海师范大学附属外国语中学董海涛名师工作室 (201600) 曾 铮

在中学数学教材中，数列位于知识点交汇处，与许多章节的内容有着密切的联系.同时，数列中蕴含着丰富的数学思想，方程与函数、分类讨论、化归和转化、数形结合等中学数学常用的思想方法在数列中都有充分的展现和应用，在数列的学习中，尤其要重视函数思想的应用，因为数列是特殊的函数.

一、从函数的角度认识数列

1、教材强化了数列定义中的函数观点

教材在给出数列的定义后，特别说明“……所以数列{an}是从正整数集N*(或它的有限子集{1,2，…，n})到实数集R的函数，其自变量是序号n，对应的函数值是数列的第n项，记为an.也就是说，当自变量从1开始，按照从小到大的顺序依次取值时，对应的一列函数值f(1)，f(2)，…，f(n)…就是数列{an} ”.在该段表述的右侧又再次以旁白的形式不惜笔墨地强调“以前我们学过的函数的自变量通常是连续变化的，而数列是自变量为离散的数的函数”.另外，在数列的表示中，教材再次强调 “与其他函数一样，数列也可以用表格和图象来表示”以及“显然，通项公式就是数列的函数解析式”.研究数列单调性的时候，又明确地加上一笔“与函数类似，我们可以定义数列的单调性”.这样不厌其烦地强调数列与函数的联系是以往教材没有过的，对比研读新教材，不难看出编者以函数思想统领数列学习的编写意图和良苦用心.

既然教材作了如此明确的说明，那么我们在数列的学习中，就应充分注意用函数的思想来研究数列中的有关问题.

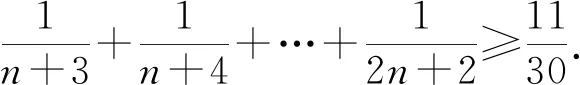
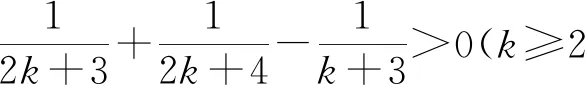
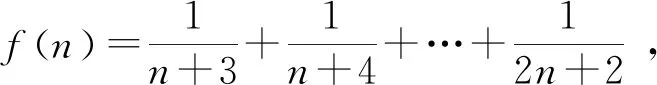
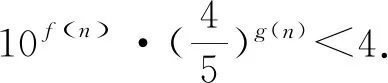
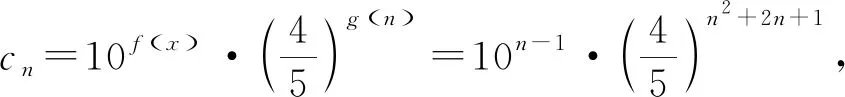
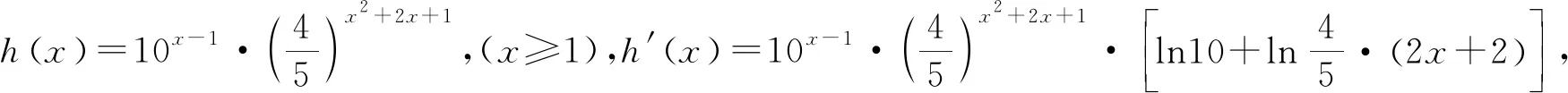
评析：解法二借助于函数的单调性巧妙地解决了数列的最大值问题，解题思路清晰简单，将数列与函数较好地统一于一体.

2、强化等差数列与一次、二次函数的联系

由于等差数列的通项公式an=a1+(n-1)d，可以变形为an=d·n+(a1-d)=d·n+b(其中b=a1-d)，从变形式中可以看出：当d≠0时，等差数列是关于n的一次函数，所以等差数列的通项an的图象是均匀地分布在一条直线上的离散点.根据两点确定一条直线，也就很容易理解为什么已知等差数列中的任意两项，可确定一个等差数列了.

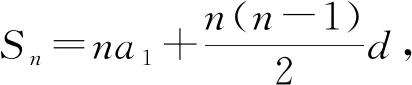
例3 一个首项为正数的等差数列，前5项之和与前13项之和相等，那么这个数列的前多少项之和最大？

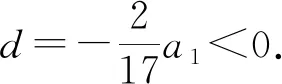
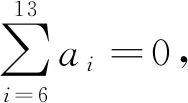
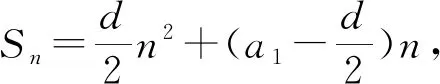
评析：解法一虽然常规但运算量大，解法二有一定的运算化简技巧性，解法三与解法四运用了函数的知识，思路清晰且运算量较少，尤其是解法四，体现了数形结合思想在解决等差数列前n项和最值问题中的作用.

3、强化等比数列与指数型函数的联系

例4 首项为正数的等比数列{an}的前n项和为80，前2n项和为6560,且在前n项和中数值最大的项是54，求此数列的首项a1和公比q.

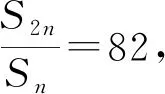
评析：这里确定an=54是关键，借助指数函数的单调性，从而使难点轻而易举地得以突破.

二、不能将函数与数列混为一谈

前面我们阐述了数列与函数的联系，看到了二者高度的统一性，体验了函数思想对数列解题的指导性，但也要看到数列毕竟是特殊的函数，又不能把数列问题完全函数化，二者还是有区别的，先看一个经典的例题：

例5 已知{an}是递增数列，且对任意的n∈N*，都有an=n2+λn恒成立，求实数λ的取值范围.

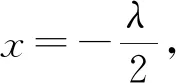
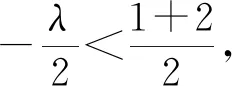
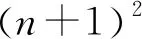
由此可见，将数列问题简单地函数化，也容易出现不和谐的音符，在涉及数列单调性问题时，我们首先要选用数列单调性自身的性质解题，以免出现类似例5的错误.为了更清楚地说明数列与函数的区别，下面我们再分析一个例题.

例6 已知数列{an}的通项为an=n·an(0an+1对所有正整数n均成立，求实数a的取值范围.

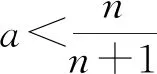
评析：两种解法的结果相距甚远.但同样的思路，例2却能殊途同归，这是怎么回事呢？实事上，在例2中已出现了不和谐的“音符”，解法一中n>3.7，解法二中n<4.16，只是由于n∈N*，将二者统一于n=4,但解题过程并未能遮盖住两种解法的些许差异.本例中，f(x)在[1，+∞)上为减函数只是an>an+1，n∈N*恒成立的充分不必要条件，并不是等价条件.

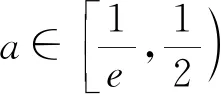
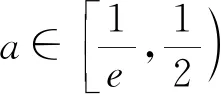
综上，学习数列，不能离开函数思想方法的指导，因为数列是特殊的函数；但在数列的学习中，也不能将自变量离散变化的数列完全等同于自变量连续变化的函数，毕竟，数列是特殊的函数.