模糊线性/非线性自抗扰切换控制及其应用

吴正平，邓聪,*，文海

1. 三峡大学 电气与新能源学院，宜昌 443002

2. 中国船舶集团有限公司第710研究所，宜昌 443003

干扰弹在飞行的末段需要单独调整弹体滚转角去对准敌方目标，进而准确地释放干扰信号，实现干扰作战的目的[1]。因此，弹体滚转通道的稳定性与迅速调整滚转角的能力是能够达到干扰弹作战目的的重要一环。通常的战场态势是导弹来袭方向任意，风向任意[2]，现代作战武器的不断升级，使得干扰弹所需跟踪的期望输入也愈发的复杂，飞行过程中由于内部结构不确定性而产生的内扰以及外部环境产生的各式的摩擦力矩都加大了弹体滚转角控制的难度。

对于干扰弹末段只需调整滚转角的情况，可以假设俯仰和偏航动力学是解耦的，这大大简化了设计[3]。对于弹体滚转通道的控制方法，有了许多的尝试，文献[4]使用状态空间分析来设计横滚回路控制器，文献[5]提出了一种直观的多项式控制方法，文献[6]使用了PID通道控制方法去控制目标的滚转运动，文献[7]提出了一种模型参考的变结构控制方法，文献[8]将神经网络预测加入制导律的设计中，文献[9]提出了一种模糊自适应PID的弹体纵向控制系统设计方案，文献[10]提出一种高阶滑模控制方案，文献[11]通过采用弹体滚转前馈补偿的两框架导引头，获得了较好的制导精度，文献[12]通过设计线性二次调节器内回路，H∞鲁棒控制器外回路的方法实现了对拦截弹的控制。但上述方法中有的抗扰性不强，有的会要求模型精确已知，有的在线计算量过大，也由于实际系统中的非线性特性难以建模，会使得控制问题更加复杂，使得上述方法在实际系统的表现不够好。基于以上现状，文献[13]引入了非线性自抗扰控制器进行弹体姿态控制，使得控制系统具备了一定的抗扰性。

文献[14]提出了一种非线性自抗扰控制器，它具有抗扰性强、跟踪精度高等优点，但其中的非线性函数会让参数整定和稳定性分析变得困难。因此，文献[15]提出了用带宽法去实现的线性自抗扰控制器，在参数整定与稳定性分析上提供了便利。文献[16-17]提出了一种线性/非线性自抗扰切换控制器，它能够综合非线性与线性自抗扰控制器的优点。但本文认为，其切换条件还有可以改进的地方。

本文通过对所建立的干扰弹滚转运动模拟装置的结构分析，建立了数学模型；通过对自抗扰控制的分析，提出一种模糊线性/非线性自抗扰切换控制器；然后对于滚转角控制系统选择了内环线性自抗扰控制器实现对飞轮角速度的快速控制，外环模糊线性/非线性自抗扰切换控制器实现对滚转角的高精度控制。最后，通过仿真模型和实验平台实验验证了控制策略的可行性与有效性。

1 基本结构与数学模型

目前的弹体滚转控制系统的数学模型是针对一个干扰弹滚转运动模拟装置而建立的，其示意图如图1所示。本文的实验对象干扰弹滚转运动模拟装置核心部件为反作用飞轮、滚转本体(弹体)、旋转翼等。反作用飞轮由伺服电机、伺服驱动器、角度检测电路、反作用飞轮轮体等组成。旋转翼用来加大飞轮的转动惯量，增加飞轮的控制范围。弹体用来配置转动惯量与实际干扰弹情况一致。

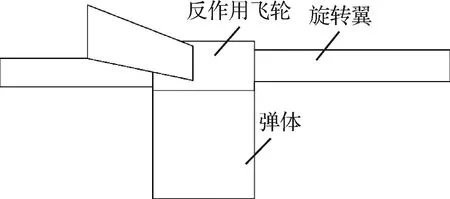
图1 干扰弹滚转运动模拟装置示意图Fig.1 Schematic diagram of roll motion simulation device of jamming bomb

1.1 数学模型

弹体滚转控制系统通过电压控制伺服电机的转速，电机产生控制力矩使飞轮转动，飞轮带动弹体转动，进而控制滚转角的变化。

直流力矩电机的电压平衡方程[18]通常描述为

(1)

式中：La为电机电枢电感；Ra为电枢阻抗；ia为电枢电流；Km为电机反电动势常数；Ωm为电机转子的转动角速度；U为电枢电压。

电机力矩与电枢电流成正比，并满足：

(2)

式中：Tc为滚转控制装置电机产生的控制力矩；Jm为滚转控制装置电机的转动惯量；bm为电机的粘滞摩擦系数。

电机产生的控制力矩Tc会引起反作用飞轮的角速度的变化，有

(3)

对弹体滚转通道,由角动量守恒定理可知

(4)

式中：Jb为滚转本体的转动惯量；a为摩擦系数；θ为滚转角；Jw为反作用飞轮的转动惯量；Ωw为反作用飞轮角速度；Md为干扰力矩。

由于电机驱动飞轮时的扰动复杂度相比较低、内环控制精度要求不高但对实时性要求较高[19]，本系统选用线性自抗扰控制器作为飞轮角速度内环；滚转角的控制在实际情况中会受到的扰动相对复杂的多[20]，选用模糊线性/非线性自抗扰切换控制器作为弹体滚转角外环。滚转角串级控制框图如图2所示，其中θ0和θ分别为期望的滚转角与实际的滚转角，Tf1和Tf2均为干扰力矩。

图2 弹体滚转角控制系统框图Fig.2 Block diagram of missile roll angle control system

1.2 状态空间表达式的建立

将式(2)和式(3)联立，可得

(5)

(6)

令x1v=yv，x2v=fv，可得飞轮角速度控制系统的扩张状态空间表达式为

(7)

(8)

(9)

(10)

(11)

2 模糊线性/非线性自抗扰切换控制设计

2.1 非线性自抗扰控制器的设计

非线性自抗扰控制器由跟踪微分器、非线性扩张状态观测器和非线性状态误差反馈控制器组成[21]。非线性自抗扰控制器的优点是跟踪精度高，抗小幅度干扰的能力强，在误差较小时，跟踪速度更快。以式(10)与式(11)所示的滚转角控制系统的扩张状态表达式为例，进行三阶非线性自抗扰控制器的设计。

(12)

式中：exp为给定值;v11为过渡过程实际给定值;v21为过渡过程实际给定值的微分;h为积分步长;r为速度因子;β1、β2、β3为观测器的增益系数;α1、α2、δ为fal函数可调参数;kp、kd为控制器增益。

非线性fhan(m1,m2,r,h)函数形式为

(13)

非线性fal(ei,αi,δ)函数形式为

(14)

2.2 线性自抗扰控制器的设计

线性自抗扰控制器由跟踪微分器、线性扩张状态观测器和线性状态反馈控制器组成。线性自抗扰控制器的优点是跟踪速度快，抗大幅度干扰的能力强。以式(10)与式(11)所示的滚转角控制系统的扩张状态表达式为例，进行三阶线性自抗扰控制器的设计。式(7)与式(8)所示的飞轮角速度控制系统是一阶系统，且在更追求控制速度情况下就不必设计跟踪微分器，只需设计二阶线性扩张状态观测器与控制器即可[22]，就不再赘述。通过“带宽法”将观测器极点配置在-ω0，可得如下线性自抗扰控制器形式：

(15)

2.3 模糊切换策略

线性/非线性自抗扰切换控制实质上是线性/非线性扩张状态观测器、线性/非线性控制器之间的硬切换，难以在整体上把握住在特定范围内线性/非线性自抗扰控制各自的优势。模糊线性/非线性自抗扰切换控制在整体上综合考虑线性自抗扰控制抗幅值较大的干扰能力更强，跟踪速度更快，以及非线性自抗扰控制的跟踪精度更高，抗小干扰能力更强等优点来引入模糊规则对线性/非线性自抗扰切换控制进行改进。防止选取ek、e、z3的某一确定值切换时出现的控制量突变导致跟踪曲线变缓的情况，削弱了切换过程中的抖动与跳变，可以实现线性与非线性自抗扰控制间的平滑切换。

模糊规则与切换形式如下：

If|ek|is S, thenUNLADRCis B, andULADRCis S;

If|ek|is B, thenUNLADRCis S, andULADRCis B;

If|e|is S, thenUNLADRCis B, andULADRCis S;

If|e|is M, thenUNLADRCis M, andULADRCis M;

If|e|is B, thenUNLADRCis S, andULADRCis B;

If|z3|is S, thenUNLADRCis B, andULADRCis S;

If|z3|is M, thenUNLADRCis M, andULADRCis M;

If|z3|is B, thenUNLADRCis S, andULADRCis B.

其中:|ek|为系统状态误差的绝对值;|e|为观测器跟踪误差的绝对值;|z3|为干扰值的绝对值作为模糊控制的输入，语言变量S、M和B分别表示小、中和大;UNLADRC表示非线性自抗扰输出的控制量权重;ULADRC表示线性自抗扰输出的控制量权重;|ek|、|e|、|z3|、UNLADRC和ULADRC的隶属度函数如图3所示。

图3 隶属度函数图Fig.3 Membership function graph

其中隶属度为0或1的点需根据实际被控对象来进行调整，选取合适切换区域。采用Mamdani方法进行推理，最后采用重心法对UNLADRC和ULADRC进行计算。在得到分别所占权重后需要进行归1化处理才是模糊切换最终的输出，再将NLADRC与LADRC实际计算的控制量与各自所占权重相乘后求和得最终的控制量输出。

2.4 具体步骤

提出一种模糊线性/非线性自抗扰切换控制器，具体设计步骤如下：

步骤1首先根据被控对象的基本原理得出数学模型。

步骤2分别建立线性自抗扰控制器与非线性自抗扰控制器。

步骤3使用带宽法对线性自抗扰控制器进行参数整定，经验法对非线性自抗扰控制器进行参数整定。

步骤4分别对被控对象进行控制，找出NLADRC跟踪更快的状态误差区域、抗干扰性更强的干扰区域，进而确定隶属度为0或1的点，制定模糊规则。

步骤5根据模糊切换规则得到NLADRC与LADRC的控制量权重值，进而得到实际的控制量输出值。

3 实验分析

3.1 仿真实验

由于线性自抗扰对电机的快速控制易于实现，就不在仿真实验中进行描述。只搭建了式(4)所示的外环滚转角控制的二阶系统进行仿真实验，系统所取参数为：反作用飞轮的转动惯量Jw=0.078 kg·m2，滚转本体的转动惯量Jb=0.026 kg·m2，摩擦系数a=0.8。

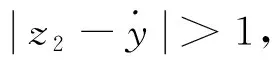
1)在t=1 s时，给定期望的阶跃输入100°，不添加扰动，所得跟踪曲线如图4所示。可见模糊切换控制的调节时间更短，精度也更高。

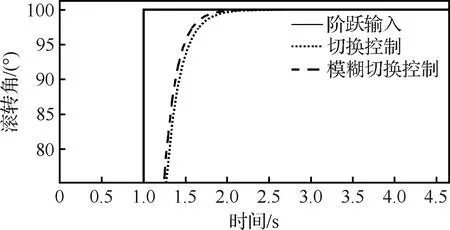
图4 无扰动情况下阶跃响应曲线Fig.4 Step response curves without disturbance

2) 在t=1 s时，给定期望的阶跃输入100°，同时在t=5 s时，添加幅值为15的阶跃扰动，即可视作小扰动，所得跟踪曲线如图5(a)所示。可见模糊切换控制的抗小扰动的能力更强。

3) 在t=1 s时，给定期望的阶跃输入100°，同时在t=5 s时，添加幅值为60的阶跃扰动，即可视作大扰动，所得跟踪曲线如图5(b)所示。虽然模糊切换控制在t=5 s时滚转角所受影响较大，但还是可以更快的达到跟踪精度。

图5 小扰动和大扰动情况下阶跃响应曲线Fig.5 Step response curves with small and large disturbance

3.2 实验验证

搭建如图6所示干扰弹滚转运动模拟装置，图6中1表示旋转翼与反作用飞轮相连接，可增大其转动惯量，2用来配置转动惯量，与实际被控对象的转动惯量一致。

图6 干扰弹滚转运动模拟装置Fig.6 Roll motion simulation device of jamming bomb

首先,手动将弹体滚转角角度调整至0°，在1 s、6 s、11 s、15 s时依次给90°的阶跃输入，分别用模糊切换控制与切换控制去做阶跃响应实验，所得响应曲线如图7所示。图中6 s到11 s中出现的角度跳变是由于将180°与-180°视为同一角度而产生的，可见在每一个阶跃响应阶段，模糊切换控制的超调量都比切换控制的超调量要小，且调节时间更短，具有更好的控制效果。

图7 连续阶跃响应曲线Fig.7 Continuous step response curves

4 结 论

1) 本文针对弹体滚转角控制系统的强非线性、滞后性、模型不确定性等特点，提出滚转角线性自抗扰控制外环、飞轮角速度模糊线性/非线性自抗扰切换控制内环的双闭环控制策略。

2) 用模糊规则去对线性/非线性自抗扰切换控制器进行改进，实现更为平稳的模糊软切换，并提出了设计模糊线性/非线性自抗扰切换控制器的基本步骤。

3) 搭建弹体滚转角控制仿真模型与干扰弹滚转运动模拟装置实验平台，将模糊线性/非线性自抗扰切换控制器与线性/非线性自抗扰切换控制器进行对比实验，得出本文设计的模糊线性/非线性自抗扰切换控制器的跟踪速度、跟踪精度、抗扰性均优于线性/非线性自抗扰切换控制器，可以提高弹体滚转角控制的性能，具有较高的实际应用价值。