基于低频阶跃脉冲的矿井低压漏电保护技术

霍耀佳，马莉，李晔，吴杨，韩利

（国网宁夏电力有限公司电力科学研究院，宁夏银川 750011）

0 引言

煤矿作为一级负荷，保证其安全生产尤为重要。由于煤矿井下环境恶劣，空气潮湿，随着开采的深入，井下温度与湿度都将越来越高[1]，如果电气设备和电缆长时间工作于这种环境下，其绝缘必然会因受潮而加速老化，导致电网对地绝缘电阻急剧降低，尤其是处于采掘工作面的电缆，受到挤压或者碰撞的概率较大，更容易造成漏电事故，在漏电故障类型中，单相漏电故障发生的比例远远高于其他类型的漏电，约占70%左右[2]。由于我国煤矿井下低压供电系统全部为中性点不接地系统，而中性点不接地系统属于小电流接地系统，发生接地故障后特征量的量值比较小，容易造成漏电装置判不出来或者误判，从而产生误动、拒动，一旦发生单相漏电故障，如果不能及时识别并切除故障，极易引发人身触电伤亡、瓦斯和煤尘爆炸等重大煤矿安全事故[3]。长期存在的漏电流还会加剧电缆绝缘的恶化，直至发生单相接地、两相短路等电网事故，严重威胁矿井电网的运行安全。根据文献[4]中规定，井下低压馈电线上，必须装设检漏保护装置或者有选择性的漏电保护装置，保证自动切断漏电的馈电线路。煤矿井下应用最广泛的附加直流检测式漏电保护方法由于不具有选择性，在发生漏电故障后，需要断开与之相关的所有线路，大大影响了煤矿井下的正常生产和通风[5]。为使系统在发生漏电后准确进行绝缘检测并且能够可靠切除故障线路，从而减小停电面积，因此研究矿井低压供电系统的漏电保护方法具有重要的理论意义和实用价值。

1 矿井低压供电系统

1.1 矿井低压系统的结构

矿井1 140 V 低压供电系统结构如图1 所示。DW0为采区变电所的低压总自动馈电开关，DW1-DW3为采区变电所的分支自动馈电开关，QC1-QC3为工作面配电点的电磁起动器，M1-M3为负载。

图1 矿井低压系统结构

对于矿井小电流接地系统，常以1 台移动变电站作为独立电源带动多条线路运行，采用放射式和干线式结合的混合式供电方式。这种方式容易实现工况自动化，漏电故障发生后停电面积较小，继电保护原理简单，并且易于动作值的整定，同时造价较低，因此被广泛应用，但是各线路长短、电力设备负载不尽相同，造成了矿井供电系统的结构多样性和复杂性[6]。随着设备容量的提升，系统电压等级不断在提高，井下低压供电系统用于各采掘工作面的供电，其电压等级主要有380，660，1 140 V。由于煤矿井下的作业环境恶劣，伴有潮湿、空间狭小等特点，且存在瓦斯爆炸的风险，因此输电线路必须采用矿用电缆，且一些电力设备都要加装隔爆外壳[7]。

1.2 漏电种类及动作值整定

根据煤矿井下电网的实际情况，漏电故障可分为集中性漏电和分散性漏电两类[8]。集中性漏电，是指发生在电网中某一处或某一点，而其余部分的对地绝缘水平仍然正常的漏电，分散性漏电，是指整条线路或整个电网的对地绝缘水平均匀下降到低于允许水平的漏电[9]。集中性漏电又分为长期集中性漏电、间歇集中性漏电和瞬间性漏电三种类型[10]。

矿井单相漏电动作整定值是根据人身触电安全电流进行整定的，对于交流系统人身能够承受的最大电流有效值IH为30 mA，人身电阻RH通常取1 kΩ，因此在系统发生漏电后流过人身的触电电流为

从而可以得到单相漏电时的动作整定R值为

对于矿井低压供电系统，以常用的电压等级为例，得到单相漏电动作电阻整定值，如表1所示。

表1 不同电压等级下的单相漏电动作整定值

2 附加阶跃脉冲信号技术

由于煤矿三相交流系统中采用附加直流检测式漏电保护的方法不具有选择性[11]，本文依据此现状，拟向系统注入一低频阶跃脉冲信号，利用其表现在线路上的特征分量来实现矿井三相交流低压供电系统的绝缘检测技术和故障选线技术。

2.1 附加阶跃脉冲信号技术原理

向系统注入的阶跃脉冲信号表达式为

式中：U—阶跃脉冲信号的峰值电压，V；

T—阶跃脉冲信号的周期，s。

式（3）经快速傅里叶变换（fast Fourier transform,FFT）后可以得到输出方波电压信号的瞬时表达式为

由式（4）可以看出，阶跃脉冲信号由正弦奇次（2n-1，n=1，2，……∞）谐波构成，即同时含有直流和交流成分。以n≤3 为例，阶跃脉冲信号的组成结构如图2所示。

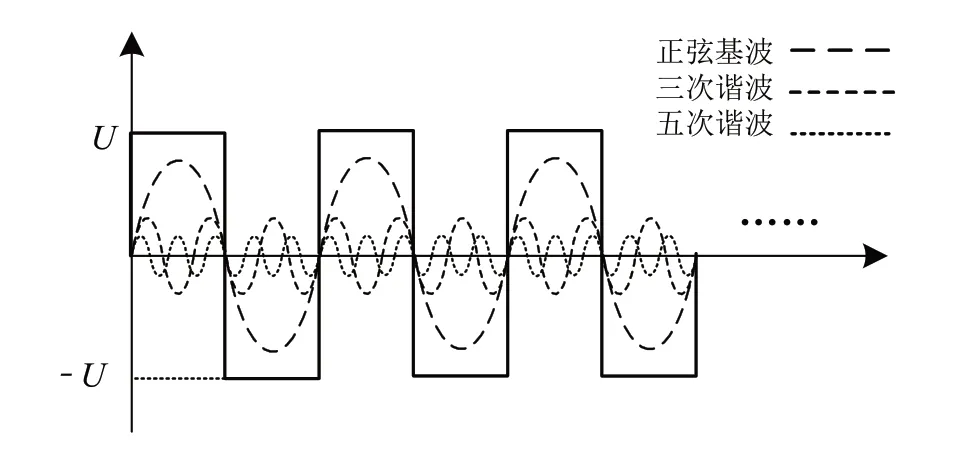
图2 阶跃脉冲信号的基本结构

当矿井低压系统发生漏电故障时，拟向系统注入阶跃脉冲电压信号，利用其直流、交流分量作用于线路后产生的特征值实现漏电保护。

由式（4）可以得到：

进而可以得到：

由式（6）可以看出，组成阶跃脉冲的基波正弦幅值是2n-1 次谐波幅值的2n-1 倍，而2n-1 次谐波频率是基波正弦频率的2n-1倍。

2.2 阶跃脉冲信号注入架构

在三相交流系统变压器出口侧注入阶跃脉冲信号，如图3 所示。为了保证阶跃脉冲信号不被原有工频信号干扰，应设置阻波电路，同时也需尽可能保证阶跃脉冲信号最大程度地输送到线路上，应设置滤波电路[12]。本文采用无源LC滤波、阻波电路，如图4所示。

图3 阶跃脉冲信号注入架构

图4 无源LC滤波阻波电路

为了阻挡工频信号，应使阻波电路对工频信号的等效阻抗呈现为无穷大，即C2和L2发生并联谐振，设工频信号角频率为ωg，则有

对于阶跃脉冲信号，应使滤波电路对所需阶跃脉冲频率的等效阻抗呈现为无穷小，即C1与C2、L2的并联发生串联谐振，L1与C2、L2的并联发生串联谐振，设需要用到基波频率ω1和任意2n-1 次谐波频率ω2n-1，则有

化简可以求得C1，L1分别为

因此，所述的滤波电路对于注入阶跃脉冲信号的基波与2n-1 次谐波信号的总阻抗接近于0，而对于工频信号的总阻抗接近于无穷大，从而达到滤波和阻波两方面的作用。

由于向系统注入的低频阶跃脉冲信号幅值小、频率低，且通过滤波器的频率均低于工频，因此对原三相交流的影响较低，利用MATLAB 仿真软件，通过对加入信号注入后原系统的线电压进行测量得到波形如图5 所示，其各次谐波含量如图6所示。

图5 注入后交流系统线电压波形

图6 交流系统线电压基波及各次谐波含量

可以看出，向系统注入的低频阶跃脉冲信号对原三相交流电压几乎无影响，波形无毛刺、成分无谐波，解决了原系统和注入信号之间的相互干扰问题。

2.3 漏电保护技术

向系统注入阶跃脉冲信号后，由于滤波电路对阶跃脉冲的特定频率信号阻抗呈现为无穷小，因此在漏电故障发生后得到等效电路，如图7所示。

图7 漏电等效回路

根据电路并联关系，可以得到阶跃脉冲基波和2n-1 次谐波电压下流过故障线路的电流有效值Ig和非故障线路的电流有效值Ifg1，Ifg2。

阶跃脉冲基波作用下：

阶跃脉冲2n-1次谐波作用下：

设Kg=Ig（1）/Ig（2n-1），Kfg1=Ifg1（1）/Ifg1（2n-1）,Kfg2=Ifg2（1）/Ifg2（2n-1），联立式（10）、式（11）可得：

由式（12）可以看出，当Rd趋近于无穷时，即未发生漏电故障时，Kg趋近于1；当Rd趋近于0时，即发生金属性接地故障时，Kg趋近于2n-1。

2.3.1 绝缘检测技术

根据式（12）所示，故障线路零序电流Ig基波和2n-1 次谐波的有效值之比Kg和漏电阻Rd存在一定关系，进而可以根据Kg反推出Rd的大小为

在漏电故障发生前，注入阶跃脉冲信号的频率，用到的谐波次数已知，各线路长度不变即分布电容一定；在漏电故障发生后，便可根据采样零序电流基波与2n-1 次谐波有效值之比Kg实现绝缘检测。

2.3.2 故障选线技术

由式（13）可以得到在漏电故障发生前后，非故障线路的零序电流基波与2n-1 次谐波有效值之比与Rd无关，恒为1；而故障线路在漏电故障发生前，即Rd趋近于无穷时和非故障线路所得比值相同也为1，但在漏电故障发生后，故障线路的Kg值介于1～2n-1 之间，表现为大于1，因此可以得到故障选线判据：

3 仿真验证

搭建基于阶跃脉冲注入的1 140 V矿井低压系统漏电保护仿真实验模型，如图8所示。注入阶跃脉冲的幅值为±24 V，频率避开工频信号为5 Hz，限流电阻为50 Ω，各线路对地绝缘良好，1号、2号、3号线路每相对地分布电容分别为0.3，0.8，0.5 μF。根据煤矿安全规定，结合人身触电安全电流30 mA·s，1 140 V 三相交流系统的单相漏电动作整定值为20 kΩ，在1.5 s 时刻在1 号线路发生A相20 kΩ 漏电故障，分析所提出漏电保护方法的正确性与可靠性。

图8 仿真模型

3.1 绝缘检测技术

以n=3 为例进行分析，在系统1 号线路（每相分布电容为0.3 μF）发生A 相20 kΩ 漏电故障前后，对故障线路首端的零序电流进行采样，利用FFT 对以阶跃脉冲注入频率为基的基波分量和5次谐波分量进行提取，得到二者有效值之比如图9所示。由图9可以看出，在1.5 s时发生20 kΩ 漏电故障后，Kg值由1上升至1.916并达到稳定，利用式（13）可以计算得到漏电阻值为19 988.53 Ω，与20 kΩ的相对误差为0.06%，验证了利用阶跃脉冲的特点实现绝缘检测公式的正确性。

图9 漏电前后故障线路Kg的变化

为了验证不同漏电阻下绝缘检测方法的精度，在0～1 MΩ 范围改变漏电阻Rd的大小，仿真实验得到n=2～4 下的Kg值，并计算得到Rdj值，计算值与真实值Rd二者之间的误差如表2所示。

从表2 可以看出，在系统发生两个极端的漏电故障时，无法准确检测出漏电电阻的大小，只能识别出漏电程度，对于Rd＜1 kΩ，Rd＞200 kΩ 的漏电故障，由表中数据结果显示在n取不同值时存在相对误差超过5%的情况；对于1 kΩ≤Rd≤200 kΩ 内的漏电故障，利用式(13)可以准确检测出漏电阻值，且相对误差在4%以内，进一步证实了此方法进行绝缘检测的可行性。

表2 绝缘检测误差分析

3.2 故障选线技术

图10 所示为1 号支路A 相发生20 kΩ 漏电故障前后故障线路和非故障线路的K值变化。在漏电故障发生前，各线路K值一致，恒为1，即证明此时未发生漏电故障；在漏电故障发生后，故障线路K值上升并达到稳态值，而非故障线路无任何变化，仍然为1，故障线路Kg值在非故障线路Kfg值的上方，因此可以判定1 号为故障线路，2 号、3号为非故障线路，验证了利用阶跃脉冲特征进行故障选线的有效性。

图10 漏电前后各线路Kg的变化

3.3 多因素对Kg的影响

为了验证漏电检测、故障选线方法的普适性，需要在不同工况下进行仿真实验验证结论的正确性，根据式（12）所示，Kg与漏电阻Rd、分布电容C1∑、低频阶跃脉冲频率f和谐波次数n有关，通过改变这4 个参数，分析对基于低频阶跃脉冲的漏电保护方法可靠性的影响。

3.3.1Rd和C1∑对Kg的影响

首先分析线路参数的影响，Rd在0～500 kΩ 范围内、C1∑在0～3 μF 范围内变化时，设低频阶跃脉冲频率为5 Hz，采用基波和5 次谐波分析得到结果，如图11所示。

图11 Rd和C1∑对Kg的影响

由图11 可以看出，Rd在0～500 kΩ 范围内、故障线路总分布电容C1∑在0～3 μF 范围内变化时，Kg均在5～1 范围内变化，即Kg随着Rd，C1∑的升高而降低，与理论计算结果一致。在Rd非常大时，分布电容对Kg的影响较小，Kg呈现为接近于1 的水平面。

3.3.2f和n对Kg的影响

分析注入阶跃脉冲模块中低频阶跃脉冲频率f和谐波次数n的影响，在2～6范围内改变n，5～30 Hz范围内改变f的大小，得到其对Kg的影响,如图12所示。

图12（a）表明当线路漏电阻为50 Ω，故障线路总对地分布电容为0.9 μF 时，阶跃脉冲频率f对Kg无任何影响，而谐波次数n的升高会导致Kg的升高，Kg呈现为一个与n线性相关的斜平面。图12（b）表明当线路漏电阻为20 kΩ、故障线路总对地分布电容为0.9 μF 时，在f一定时，Kg随着n的升高而升高，在n一定时，随着Kg的升高而减小，这主要是因为f越高，容抗越小，容性电流的成分比例升高进而使Kg减小。图12(c)表明当线路漏电阻为1 MΩ，故障线路总对地分布电容为0.9 μF 时，Kg不受f与n的影响，呈现为一个恒为1的水平面，即非故障水平面。

图12 f和n对Kg的影响

4 结论

建立了基于低频阶跃脉冲信号注入的矿井1 140 V三相交流供电系统漏电保护仿真模型，通过理论分析和仿真实验得到结论如下：

1）利用低频阶跃脉冲信号在系统各线路表现的特征能够准确实现绝缘检测，绝缘检测的误差在4%以内，能够有效检测1～200 kΩ 范围内的漏电故障，在其他范围内的计算结果误差较大。

2）故障选线方法有效排除了漏电阻、分布电容、低频阶跃脉冲频率和谐波次数的影响，线路和注入系统参数的变化仅会改变故障线路Kg的大小，而非故障线路Kfg恒为1，不影响故障选线的可靠程度。

3）向系统注入低频阶跃脉冲信号进行漏电保护的方法弥补了附加直流检测式漏电保护的不足，利用注入信号在线路上产生的特征量大小及差异实现了绝缘检测和故障选线技术，且注入方法和滤波电路构建容易，有利于提高冗余度。