高频变压器不同绕组结构对分布电容的影响

杨慧娜，柏树青

(华北电力大学 电气与电子工程学院，北京102206)

0 引 言

由于反激变换器具有以下优点:(1)电路简单，能高效提供多路直流输出，适合多组输出要求。(2)输入电压在很大的范围内波动时，仍可有较稳定的输出，无需切换而达到稳定输出的要求。(3)转换效率高，损失小。(4)变压器匝数比值较小。因此得到了广泛应用。变压器作为反激变换器中的关键部件，对变换器的整机性能有着很大影响［1］。随着应用场合输入、输出电压等级的提高，以及为适应小型化要求而采用更高开关频率的发展趋势下，反激变换器的正常运行及性能优化越来越受到其变压器寄生参数的限制［2，3］。目前对变压器寄生参数的研究中，更多是分析漏感，对于分布电容往往将其忽略，当变压器工作在低频时，分布电容的影响不大。但是随着开关电源越来越小型化，高频化，电子变压器的寄生电容会对反激变换器整体性能产生很大的影响。在开关管导通瞬间，变压器绕组分布电容中的能量发生变化，会在变压器内部及主电路中产生较大电流尖峰，影响开关管工作的可靠性。且由于分布电容的存在，它会与变压器或者元器件的寄生电感形成振荡现象，从而会造成反激变换器不可预测的一些行为特性。由于原副边绕组间分布电容的存在，提供了EMI 噪音的传导路径，从而产生严重的电磁干扰问题，影响电子产品的电磁兼容性［4～7］。除了上述提到的变压器分布电容的不利影响，还可以利用变压器分布电容作为并联谐振电容［8～10］，从而减小整个电路系统的体积。变压器分布电容会对整个电路系统的性能产生很大的影响，所以通过采用不同变压器绕组结构实现分布电容的改变来改善反激变换器整体的性能具有重大的实用价值和研究意义。

变压器绕组结构的不同影响着分布电容的大小。文献［1］针对高压输入低压输出变压器场合，研究了绕组结构的不同对变压器分布电容大小的影响，但该文献使用的方法有它的不足之处。这种方法不足主要有:(1)没有针对各种变压器绕组的不同绕法来提取具体的寄生电容参数。(2)理论上没有具体解释为什么不同的绕组结构会对变压器分布电容大小产生影响，没有针对各种不同的绕法及布局进行详细的分析。文献［2］给出了变压器分布电容对电路的影响以及变压器的等效电路模型，并提出了控制寄生电容的工程方法。文献［5］首先对求取变压器分布电容的各种不同的理论方法进行了系统的总结，并针对这些方法的不足，进行了补充。此外，基于前人的基础上，提出了变压器寄生电容新的等效电路模型。文献［8］给出了提取变压器寄生电容参数的3 种方法，第1 种方法是基于平板电容结构的解析表达式计算。该方法虽然简单，易于理解，但计算过程中，用到了很多的近似，很多实际因素没有考虑，所以该方法计算出来的寄生参数误差较大。第2 种方法是基于实验测量的方法。该方法虽然方便、简单，但是只有在变压器制造好后才能用该方法测量其分布电容参数，增加了设计的成本和时间。第3 种方法是基于有限元仿真工具的计算，也就是电磁场数值方法。

本文首先给出变压器分布电容对反激变换器的影响分析及这些分布电容的确定方法。然后，针对各种不同绕法及排列布局为什么会对变压器分布电容大小产生影响进行了深入的分析。最后，在PExprt/PEMag 软件环境下，设计不同绕组绕法及绕组排列布局的变压器模型，再把以上不同绕组结构的变压器模型导入到有限元软件Ansoft Maxwell 提取不同绕组结构的分布电容参数，根据提取的参数和理论分析的结果进行对比，从而对本文提出的方法进行了仿真验证。该方法可以考虑绕组电压分布，变压器材料及变压器结构等的影响，且不需要设计实际的变压器，就可以准确提取变压器分布电容参数。

1 变压器分布电容对反激变换器的影响

图1 是考虑寄生电容后的高压输入低压输出RCD 箝位反激变换器拓扑［11，12］。其中，L1，Lm分别表示原边漏感和磁化电感，C1_1为原边绕组分布电容，C1_2，C01_2分别表示原边与副边绕组不同接线端之间的分布电容。反激变换器的工作原理是［13］:当开关晶体管被激励导通时，输入电压加到变压器初级绕组，初级绕组流过电流。由于变压器次级整流二极管反接，次级绕组无电流流过，能量在变压器电感中以磁能的形式储存起来。当开关晶体管截止时，变压器感应电压与输入电压反相，使整流二极管导通，变压器储存的能量释放出来，供负载及电容器充电。

图1 考虑分布电容时反激变换器拓扑Fig.1 Diagram of RCD-clamp flyback converter including stray capacitances

为防止磁芯饱和，通常在变压器磁路中留有较大气隙，但这会使变压器有较大漏磁，造成较大的漏感。当功率开关管关断时，由于漏感的存在，会在开关管上激起很高的电压尖峰。漏感能量吸收方法有多种，图1 电路是采用RCD 箝位电路来吸收漏感能量，控制开关管关断电压尖峰［1］。

另外，在高压小功率场合，分布电容储能与漏感储能相当，甚至比漏感储能大，此时分布电容对电路性能影响很大。变压器分布电容对电路的影响主要有:(1)在开关转换时，绕组电压发生变化，继而分布电容中的能量发生变化，因此就会在变压器内部和主电路回路中产生高频的振荡环流，增加变压器以及功率器件的功率损耗，并且产生高频电磁辐射。如果采用峰值电流控制，将影响电流采样的正确性，从而对电源的稳压精度、稳定性以及损耗产生较大影响。因此原副边绕组的寄生电容会对电路产生影响。(2)开关管开通速度越快，绕组电压的变化速度就越快，从而绕组分布电容中的能量流动也会越快，根据i = C(du/dt)可知会形成较大电流尖峰。开关管开通速度较慢，虽然能够减小分布电容引起的电流尖峰幅值，但会使尖峰持续时间变长，为此需采用较大的滤波元件，造成电流的相移，不利于系统闭环设计。(3)变压器绕组电压越高，分布电容储存的能量越大，在开关管导通瞬间会导致原边电流前沿产生尖峰。根据i = C(du/dt)可知在电压变化率一定的情况下，变压器分布电容越大，原边电流也就越大，进而影响开关管工作的可靠性，甚至造成开关管的毁坏。(4)可以利用变压器分布电容作为并联谐振电容。所以基于以上分析，应对变压器分布电容进行合理控制。

因此，为了保证变压器在高频时具有良好的性能，必须考虑寄生参数的影响，研究影响变压器寄生参数的因素［13～15］。本文通过研究不同的绕组连接方式和绕组排列布局对分布电容大小的影响，给出了改变分布电容大小的方法。

2 分布电容的确定

2.1 绕组分布电容

根据W = CU2/2 可知绕组的分布电容与绕组中的电压分布有关，在电压大小确定的情况下，绕组中存储的电场能量越大，分布电容就越大。因此要计算同一绕组按多层绕制的层间分布电容，首先要确定绕组中的电压分布。根据静电场理论，由下式近似计算2 层绕组分布电容C 的大小:

式中:E 是2 层绕组间电场强度;ε 是层间绝缘材料介电常数;V 是1 层绕组的体积;u 是相邻层间的电压分布;d 是绕组相邻层间距;l 是绕组导线平均长度;h 是绕组高度;Uin是输入电压。式(1)给出了2 层绕组分布电容的计算，如果匝数比较多，绕组就是多层多段结构，总的绕组分布电容也可以由式(1)计算得到。

2.2 绕组间分布电容

根据静电场理论，不同绕组间的分布电容可根据C = εS/d 推导而得。由于很多变压器绕组骨架近似矩形，因此可以把变压器绕组等效成一块极板，这样就得到了平行板电容器模型，如图2所示。

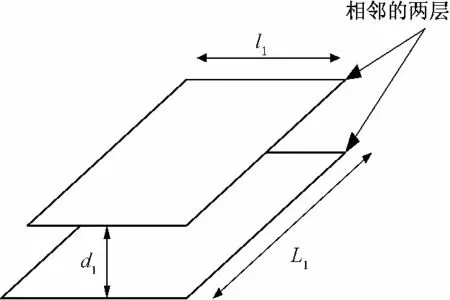
图2 平行板电容器模型Fig.2 Parallel-plate capacitor model

图3 极板的有效距离Fig.3 Effective distance between plates

如图3，两块极板之间的有效距离可表示为［9］

则原副边绕组间的分布电容可近似为

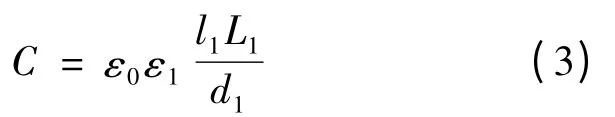
式中:ε1表示层间介质等效相对介电常数;d2表示匝与匝间的距离;h 表示层间空隙长度;对于实心圆线来说，r0等于包括绝缘的圆线的半径，对于金属箔线来说，r0等于径向长度的一半;l1表示两层绕组平均匝长;L1表示层的高度;δ 表示导线绝缘层的厚度。

有些变压器绕组的骨架是圆柱形，所以除了用平行板电容器外，还可以用圆柱形电容器来等效原副边相邻绕组层。如图4 所示:

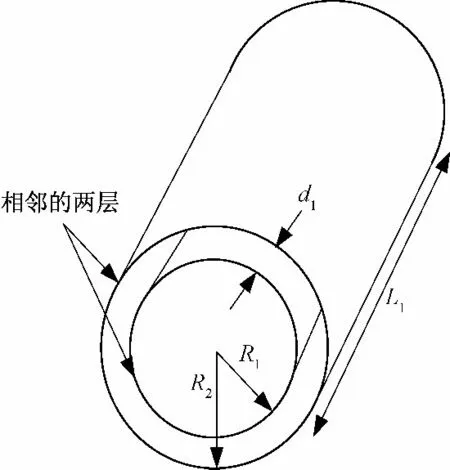
图4 圆柱形电容器模型Fig.4 Cylindrical capacitor model

则原副边绕组间的分布电容可近似为［9］

因此变压器原副边相邻绕组层可以用平行板或者圆柱形模型等效，从而近似算出2 绕组间分布电容，不过，大多数情况下都使用平行板模型。

3 绕组结构对变压器分布电容大小的影响

3.1 绕组连接方式对分布电容大小的影响

3.1.1 C 型接法

变压器绕组绕制方式主要分为C 型绕法，Z型绕法以及分段式绕法［16～19］。本文以高输入电压低输出电压反激变压器为例，因此原边匝数远远大于副边匝数，因为初级匝数较多，所以初级绕组一般要分层分段绕制。而匝间电容远远小于层间电容，因此可以忽略匝间电容。由于绕组两层之间存在电位差，所以就产生了层间电容，变压器绕组层与层之间的不同的连接方式会导致层间不同的电位差，继而产生不同大小的分布电容。图5 是绕组C 型连接示意图与电压分布图。其中，U 为初级绕组电压;w 如图所示;k 为初级绕组的层数;l 为绕组的平均匝长。绕组两相邻层之间的距离是d。层间的绝缘介质的介电常数是ε。根据文献［13］，由于高频变压器的漏磁通相比激磁主磁通完全可以忽略，所以激磁线圈每匝所交链的磁通基本相同，每匝的感应电动势，或激磁感抗也基本相同，而且每匝线圈的交流电阻一般远远小于激磁感抗，因此假设变压器线圈的电位沿绕组匝数线性分布，即每一匝线圈的电压降均相同是合理的。则根据图5 可知每层绕组两端的电压差都是U/k，绕组相邻层之间的电压随着绕组长度而变化。根据静电场理论，相邻绕组可以等效为两块平行板模型，则相邻层间电压表达式为

电场强度为

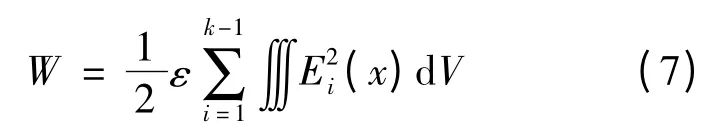
因为C 型绕法初级绕组分布电容Cs的近似表达式为

图5 变压器C 型绕组结构与电压分布Fig.5 Type C winding of transformer and voltage distributions

3.1.2 Z 型接法

Z 型绕法也就是所说的折叠绕法，即在绕完1层之后，将线端拉至第1 层的始端继续绕第2 层，依次重复。变压器绕组的Z 型绕法如图6 所示。由图6 可以看出，Z 型绕法相邻层间各处的电压差是相等的，即U(x)= U/k，则电场强度为

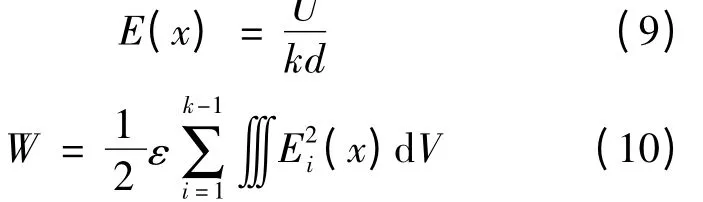
Z 型绕组分布电容为

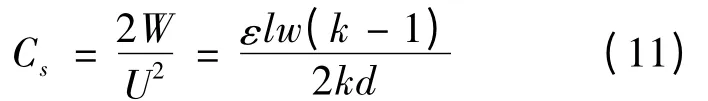
图6 变压器Z 型绕组结构与电压分布Fig.6 Type Z winding of transformer and voltage distributions

3.1.3 分段式绕法

利用分段骨架将变压器绕组匝数分成几等份，每一份绕制在一个骨架上，这就是绕组的分段式绕法。其中，q 是分段数，k 是每段绕组的层数，如图7 所示。基于以上C 型绕法分布电容的计算以及静电场理论，每段绕组的分布电容为

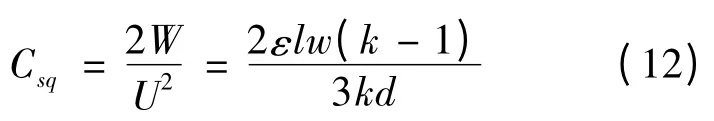
根据分段式绕组的电压分布，则初级绕组总分布电容为

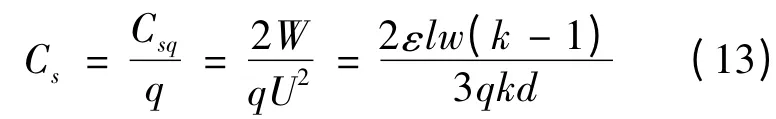
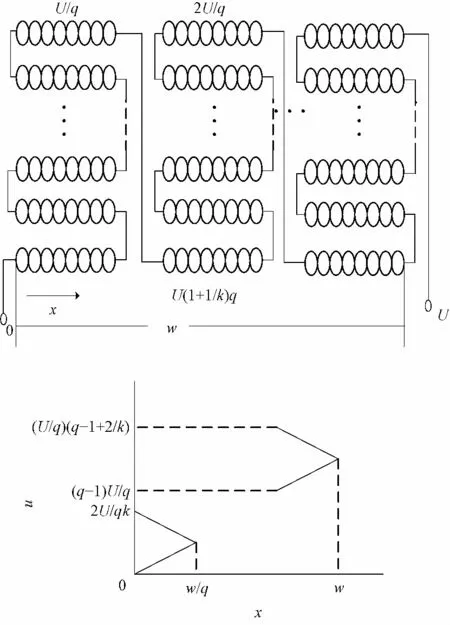
图7 绕组分段式绕法以及电压分布Fig.7 Segmentation winding and voltage distributions

基于以上对C 型接法，Z 型接法以及分段式绕法的分析可知，C 型绕法结构虽然简单，但是相邻两层相邻匝间的最大电压差大，分布电容储存的能量就比较大，从而绕组的端口等效电容较大;Z 型绕法的绕线相比C 型绕法较复杂，但是绕组相邻层相邻匝间压差比较小，对比(8)式和(11)式，Z 型绕法计算得到的分布电容是C 型绕法分布电容的3/4，可见绕组的端口等效电容明显减小。如果变压器绕组匝数很多，要进一步减小绕组分布电容，则可采用分段式绕法。由于分段式绕法是利用分段骨架将原来的绕组匝数分成相等的若干份，各段绕组间的最大电压差就只有输入电压的若干份之一，分段越多分布电容的值就越小。对比(8)和(13)式可知，把原本C 型接法的绕组分成q 段后，分段式绕组分布电容只有C 型绕法分布电容的1/q。同样，把Z 型接法的绕组分成q 段后，分段式绕组分布电容只有Z 型绕法分布电容的1/q。

3.2 绕组布局对分布电容大小的影响

除了绕组层与层间连接方式外，绕组不同的布局也会对变压器分布电容大小产生影响。绕组的布局主要有传统式布局和交错式布局，如图8 所示。

图8 传统式布局与交错式布局Fig.8 Traditional layout and interleaved layout

根据C = εS/d，由图8 可看出，采用交错布局，同一绕组层与层的实际间距增大了，所以绕组分布电容相比传统布局要小。但是采用交错布局排列后，原副边绕组正对的面积变大，初级与次级间实现了较为紧密的耦合，因此初次级绕组间分布电容相比传统布局变大，但是漏感相比传统布局就减小了，这种情况下低漏感与大分布电容就成了一对矛盾。所以，采用哪种变压器绕组排列布局，应根据实际需要折衷考虑。

基于上述分析，可以得出以下结论:(1)变压器绕组采用不同的绕法，对分布电容的大小有很大影响。分段式绕法分布电容最小，C 型绕法分布电容最大，而Z 型绕法介于中间。(2)变压器绕组采用交错式布局与未采用交错式布局相比，同一绕组层与层之间分布电容明显减小，而原副边绕组间分布电容明显增大。这是因为采用交错布局后，同一绕组层与层的距离变大了，原副边绕组正对面积也变大了。

4 仿真分析

本文用PExprt 软件设计了220 V 输入、15 V/15 W 输出，工作频率为200 kHz，采用峰值电流控制，工作于DCM 模式的反激变换器。变压器参数如表1 所示。为了验证不同绕组结构对分布电容大小的影响，本文利用PEMag 软件改变变压器绕组绕法以及排列布局，从而分别得到C 型、Z 型、分段式以及交错式布局的变压器绕组模型，把以上模型导入Ansoft Maxwell 软件提取这4 种不同绕组结构的分布电容参数。

把在PExprt 软件中建立的Z 型绕组结构的变压器模型导入到Ansoft Maxwell 软件中得到的电位分布云图如图9 所示。从图9 可得知假设变压器线圈的电位沿绕组匝数线性分布，即每一匝线圈的电压降均相同是正确的。变压器电场强度分布云图如图10 所示，从图10 得知Z 型绕法相邻层间各处的电场大小是相等的，即验证了上述公式(9)是正确的。

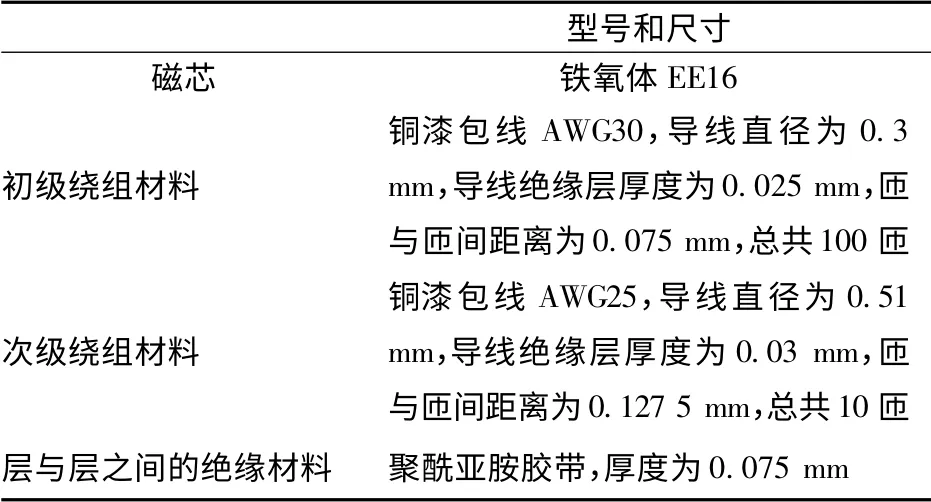
表1 变压器参数Tab.1 Parameters of the transformer

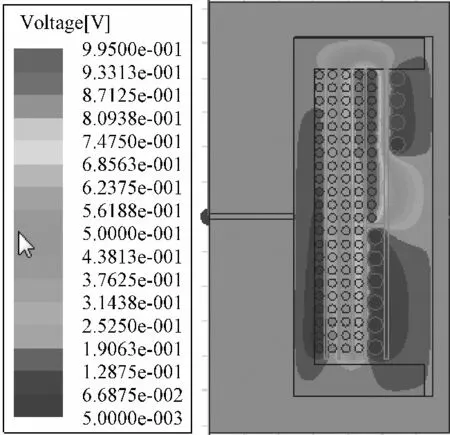
图9 变压器电位分布云图Fig.9 Voltage distribution of the transformer

图10 变压器电场强度分布云图Fig.10 Electric field intensity distribution of the transformer

由于本文采用的是高压输入，低压输出的反激式变压器，初级匝数多，次级匝数少，由于次级匝数很少，则次级绕组结构单一，所以主要研究的是匝数、层数多的高压侧绕组，也就是初级绕组。因此该文改变变压器初级绕组的绕法以及排列布局，利用Maxwell 软件提取初级绕组不同情况下的分布电容以及原副边绕组间分布电容来验证上述分析。用软件提取的5 个分布电容的电路模型如图11 所示。

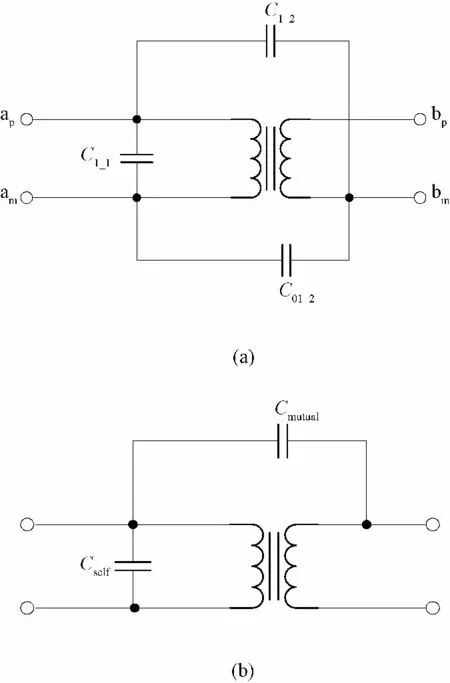
图11 软件提取的5 个分布电容参数的电路模型Fig.11 Circuit model of extracted five stray capacitances by software

基于电磁场理论，电容的存在形式可以通过假设若干个变量来表达，PExprt 软件的分布电容电路模型中假定了两个变量，ap和am间的电压，即u(ap，am)，am和bm间电压，即u(am，bm)。这两个变量均等效在一次侧，则根据静电场理论有:

从(14)式可看出有3 种能量，因此对应需要3个分布电容存储，如图11(a)所示。图11(a)的分布电容参数与图11(b)中分布电容参数的关系是，当初级电压u(ap，am)为零，级间电压u(am，bm)不为零，则

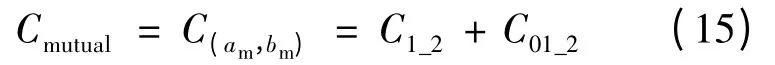
当初级电压u(ap，am)不为零，级间电压u(am，bm)为零，则

表2 是用软件提取的不同绕组结构的分布电容参数，从表2 提取的参数中，也可以直接验证式(15)和(16)的正确性。

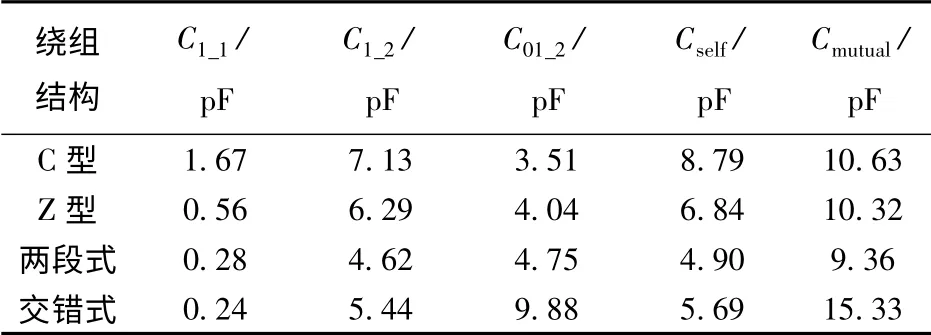
表2 不同绕组结构的分布电容参数Tab.2 Stray capacitances of different winding strategy

根据表1 中变压器参数和前面所述C 型、Z型、以及两段式绕法的初级绕组的分布电容计算公式，分别计算出相应的Cself，与软件提取的分布电容参数进行比较，如表3 所示。从相对误差上可以看出，用软件提取的初级绕组分布电容值和理论计算值基本相符。这样间接验证了表2 中用软件提取的各分布电容的正确性。

图12 是根据表2 生成的柱形图，从图中可以更直观地看出各种不同绕组结构分布电容的大小。从表中数据可以归纳出以下规律:原副边绕组都由C 型改成Z 型接法后，分布电容Cself只有C型绕法的3/4，初级绕组分布电容C1_1只有C 型绕法的1/3，级间电容Cmutual基本不变。把初级绕组由原来的Z 型接法改为两段式绕法后，初级绕组分布电容C1_1只有原来Z 型绕法的1/2，级间电容Cmutual变化不大;把原来Z 型接法再交错式排列后，初级绕组分布电容C1_1比未采用交错式布局的分布电容明显减小，而原副边绕组间分布电容Cmutual则明显增大。因此可以通过改变变压器绕组结构，达到改变其分布电容的大小的目的，经过验证，此种方法效果明显。并且以上规律与前面的理论分析十分符合，从而验证了文中分析的正确性以及这种提取分布电容参数方法的可行性。

图12 不同绕组结构的分布电容柱形图Fig.12 Bar graph of stray capacitances with different winding strategy

表3 Cself 的软件提取值验证Tab.3 Verification of by using PExprt software

5 结 论

反激变换器在高频下工作时，变压器分布电容对系统效率、开关损耗、器件应力、闭环稳定性等的影响不能忽略，尤其在输入电压很高时，分布电容的影响就更明显。除了抑制变压器分布电容外，在某些情况下，可以对变压器的分布电容加以利用，比如利用高频变压器分布电容做并联谐振电容。由于变压器分布电容大小与绕组连接方式和绕组排列布局有很大关系，因此，可以通过改变变压器绕组结构来达到改变分布电容大小的目的。随着频率的不断提高，变压器分布电容的影响就越大。所以为了得到性能良好的电路系统，设计大电压、高频率变压器时，必须考虑变压器分布电容的影响。

［1］赵志英，龚春英，秦海鸿.高频变压器分布电容的影响因素分析［J］.中国电机工程学报，2008，28(9):55 －60.

［2］赵志英，秦海鸿，龚春英.变压器分布电容对高频高压反激变换器的影响及其抑制措施［J］.电工电能新技术，2006，25 (4):67 －71.

［3］齐玮，钟和清，林磊，等.分布电容对高频高压变压器性能的影响及其控制措施［J］.通信电源技术，2008，25 (3):6 －8.

［4］宋晓婷.高频高压变压器分布参数测量和绕组结构设计［D］.大连:大连理工大学，2013.

［5］张世平.三电容分布参数高频脉冲变压器模型分析及参数测量［D］.广州:华南理工大学，2012.

［6］赵争菡.开关电源中高频变压器分布电容的分析与计算［D］.天津:河北工业大学，2006.

［7］Pramanik S，Satish L.Estimation of series capacitance for a three-phase transformer winding from its measured frequency response ［J］.IEEE Transactions on Power Delivery，2013，28 (4):2437 －2444.

［8］郭玲.开关电源共模传导EMI 的抑制［D］.天津:天津大学，2009.

［9］Biela J，Kolar J W.Using Transformer Parasitics for Resonant Converters—A Review of the Calculation of the Stray Capacitance of Transformers ［J］.IEEE Transactions on Industry Applications，2008，44 (1):223 －233.

［10］吴为麟，邹家勇，陈永延.考虑分布电容的高压直流电源谐振参数设计［J］.电力自动化设备，2009，29 (9):26 －30.

［11］Hai Y L，Zhu J G，Hui S Y R.Experimental determination of stray capacitances in high frequency transformers ［J］.IEEE Transactions on Power Electronics，2003，18 (5):1105 －1112.

［12］王全保.新编电子变压器手册［M］.沈阳:辽宁科学技术出版社，2007:388 －390.

［13］董纪清，陈为，卢增艺.开关电源高频变压器电容效应建模与分析［J］.中国电机工程学报，2007，27 (31):121 －126.

［14］Li Y，Du J P，Li X H，et al.Calculation of capacitance and inductance parameters based on FEM in highvoltage transformer winding ［C］.2011 International Conference on Electrical Machines and Systems(ICEMS).

［15］Wang Z D，Li J，Sofian D M.Interpretation of transformer FRA responses—Part I:Influence of winding structure ［J］.IEEE Transactions on Power Delivery，2009，24 (2):703 －710.

［16］Dalessandro L，Da Silveira Cavalcante F，Kolar J W.Self-Capacitance of High-Voltage Transformers ［J］.IEEE Transactions on Power Electronics，2007，22(5):2081 －2092.

［17］Massarini A，Marian K K.Self-Capacitance of Inductors ［J］.IEEE Transactions on Power Electronics，1997，12 (4):671 －676.

［18］梁利辉，董华英，梁贵书，等.VFTO 下变压器绕组电位分布的计算［J］.华北电力大学学报(自然科学版)，2009，36 (2):13 －17.

［19］Ranstad P，Nee H P.On the distribution of AC and DC winding capacitances in high-frequency power transformers with rectifier loads ［J］.IEEE Transactions on Power Electronics，2011，58 (5):1789 －1798.