不同侧出线的变压器线圈匝数计算

李建军 赵 楠

(特变电工沈阳变压器集团有限公司 辽宁 沈阳 110144)

一、前言

笔者在设计干式接地变压器及三线圈自偶变压器的时候，经常会遇到干式接地变压器的首端出头和末端出头，三线圈自偶变压器中压首端出头和末端出头分别在铁心柱的两侧的问题，这时A，B，C三相其电气匝数的核算略有不同。笔者通过模型试验所得的数据，通过理论分析和计算得出了电气匝数和所谓的实绕匝数之间的关系。如图1所示为首端出头和末端出头分别在铁心柱的两侧的线圈绕制简图。为叙述方便只画出低压线圈。下同。

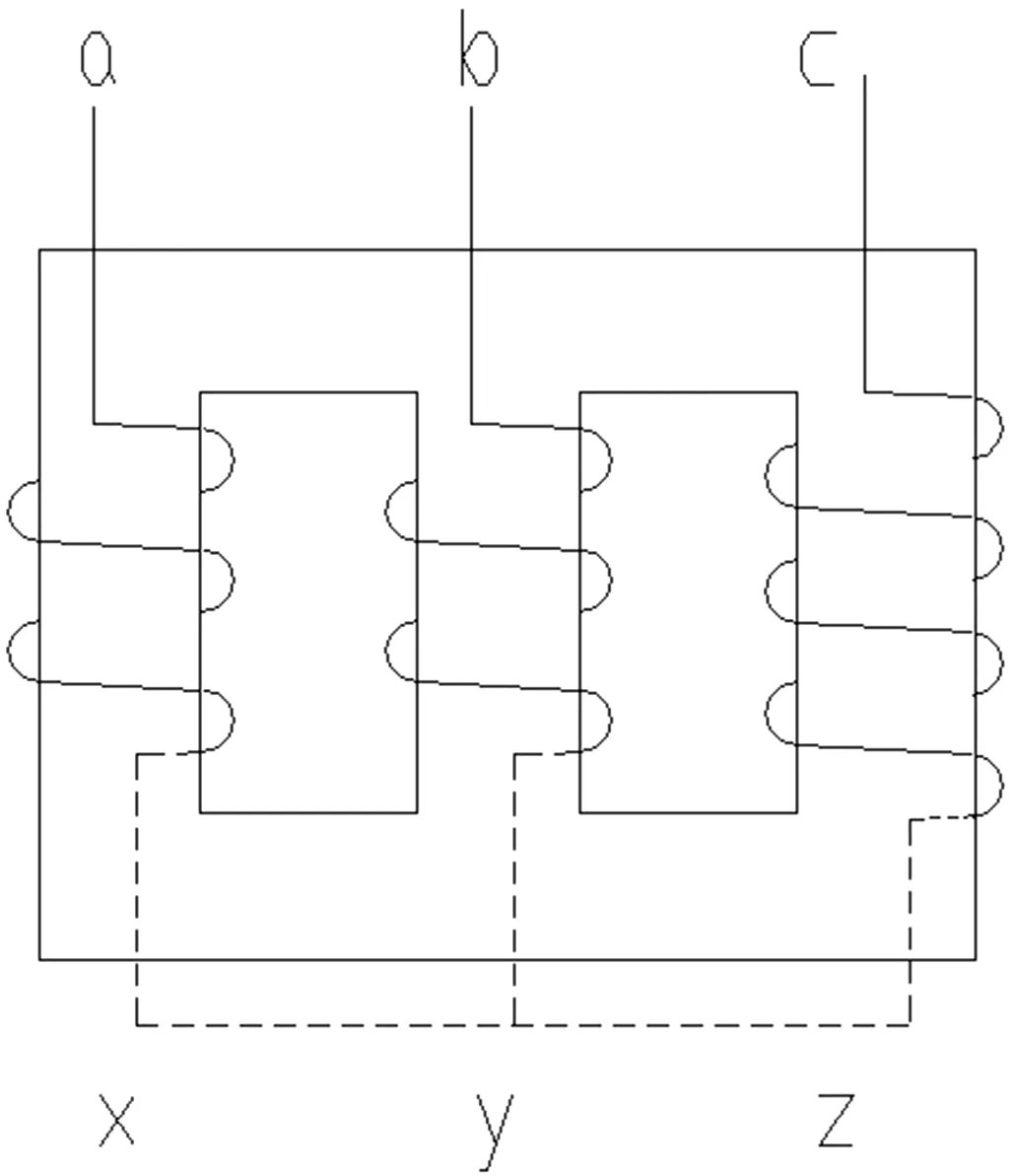
图1 线圈烧制简图

二、试验模型的建立及数据的取得

试验时取一台已叠好的三柱铁心，准备一些铜导线按如下数据缠绕在铁心柱上，高压A，B，C三相按匝数：NA=NB=NC=16匝缠绕，并且使其首尾出头在铁心柱的一侧。低压a，b，c三相按匝数Na=3匝,Nb=3(2)匝,Nc=3匝缠绕，首尾出头在铁心柱的不同侧，左绕向，接法为Yy0，如图1所示。(以上匝数的选取是为了线圈绕制方便以及所选铁心的实际情况所决定的，并不是唯一的选择)试验时高压侧施加线电压为UAB=UBC=UCA=200V,则匝电势et=UAB/ NA/1.732=200/16/1.732=7.3666v此时低压相电压实测得Ua=22.1V,Ub=19.4V,Uc=22.2V。

三、理论分析及数据计算

通过以上数据可以初步断定低压b相电压与a，c相相比较低，说明与b相线圈相交链的磁通与a，c相相比为少，但又不差一匝匝电势。这就是本文所要重点讨论的内容。我们知道，忽略三柱铁心磁路本身的不对称性，近似地认为当A，B，C三相线圈施加三相对称的正弦线电压时，铁心中各相磁通也是三相对称的正弦形磁通，在所有瞬时，三相磁通的相量和为零，即有下式成立，ΦA+ΦB+ΦC=0 ΦB=(-ΦA)+(-ΦB)

(1)

根据以上分析，由安培环路定律可知，B相线圈所交链的磁通分别为A相，C相流过B相铁心柱的磁通的相量和，如图2，图3所示。

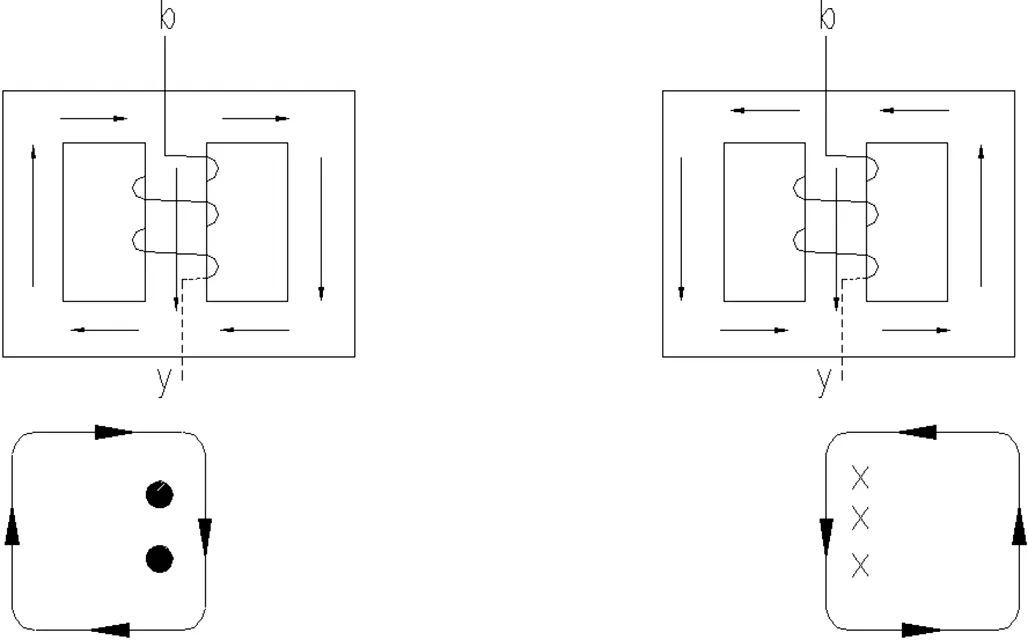
图2 A相磁通与B相线圈交链示意图 图3 C相磁通与B相线圈交链示意图

图2中B相线圈有2匝电气匝数与A相磁通交链，图3中B相线圈有3匝电气匝数与C相磁通交链，则B相线圈磁通为

ΦB=-(ΦA+ΦC)=-(2ΦA’+2ΦC’+ΦC’)

(2)

ΦA=Na’×ΦA’=2ΦA’ ΦC=Nc’×ΦC’=3ΦC’

其中ΦA’，ΦB’，ΦC’为每匝线圈产生的磁通，并且代数上ΦA’=ΦB’ =ΦC’

Na’为B相线圈与A相磁通交链的匝数，Nc’为B相线圈与C相磁通交链的匝数。由式(2)可画出图5相量图。

图4 三相对称磁通相量图 图5 磁通相量合成图

由图4及图5可得 ΦB=2ΦB’+(-ΦC’)，这里-ΦC’作为整体参与到计算中，“-”可以略去。

ΦB =2.6457ΦC’=2.6457ΦB’ =2.6457ΦA’

(3)

由式(3)可得 Ub=2.6457×7.3666=19.49V≈19.4V,此值与实测值基本相符。

以上计算说明首端出头和末端出头分别在铁心柱的两侧的B相低压线圈其电气匝数既不是3匝也不是2匝而是其相量和。

四、结论

通过上面的实际模型的测量及理论分析我们得出首端出头和末端出头分别在铁心柱的两侧的B相线圈其电气匝数是B相线圈分别与A，C相与B相闭合回路磁通相交链的匝数的相量和的结论。一般情况下可用下式表述：

ΦB2=(Na’×ΦB’)2+((Nc’-Na’)×ΦC’)2-Na’×(Nc’-Na’)×2×ΦB’× ΦC’cos120°

=(Na’×ΦB’)2+((Nc’-Na’)×ΦB’)2+Na’×(Nc’-Na’)ΦB’2

=((Na’)2+(Nc’-Na’)2+ Na’×(Nc’-Na’))ΦB’2

ΦB=ΦB’×((Na’)2+(Nc’-Na’)2+ Na’×(Nc’-Na’))0.5

即Nb=ΦB/ΦB’=((Na’)2+(Nc’-Na’)2+ Na’×(Nc’-Na’))0.5

(4)

式(4)即是首端出头和末端出头分别在铁心柱的两侧的B相线圈其电气匝数的计算公式。同理也可分析出a,c相电气匝数的计算，只是其匝数只与本相铁心柱内磁通交链次数有关，没有相量合成的问题，这里不再详述。

下面举例说明B相线圈电气匝数的实际计算。一台OSFS9-180000/220/118/35的中压线圈共494匝，匝电势et=118000/494/1.732=137.9021V。

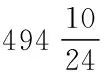
应用式(3)可得

Nb=ΦB/ΦB’=((494)2+(495-494)2+494×(495-494))0.5=494.5

即B相线圈的电气匝数为494.5匝。其感应电势为494.5×137.9021=68192.6V，变比误差为68192.6×1.732/118×100%=0.0957%，满足变比误差小于0.25%的要求。

通过应用式(3)我们可以很容易算出B相线圈首尾不同侧出头的电气匝数，进而进一步核算其变比误差。