水平翅片管外凝结液膜分布及换热特性影响研究

李慧君，董 楠

(华北电力大学能源动力与机械工程学院，河北保定071003)

0 引言

凝结换热在许多领域中存在，换热器的换热性能直接影响能源利用率，肋片管是管壳式换热器中普遍采用的换热管，肋片管外的凝结换热研究对提高换热器设计性能，减小换热器制造材料等起到重要作用［1］。强化管外的凝结换热研究广泛集中在理论分析和试验研究:Beatty 和Katz 假设重力为肋片管上凝结液迁移主要驱动力，忽略表面张力作用和肋顶换热，建立了首个二维表面低肋管的凝结换热系数计算式［2］，Cheng 通过试验获得R134a 在较高肋密度的肋管上的凝结换热系数值，该值比该模型计算值高很多［3］，表明该模型仅适用肋片密度低的肋片管，其适用范围受到很大限制;Karkhu 和Borovkov 指出表面张力导致的液膜压力梯度是其在肋侧壁上迁移的主要驱动力、同时考虑凝液淹没对肋表面换热的不利影响，给出肋管外凝结换热系数计算式［4］，但该模型与自然对流冷凝换热的实际情况仍有较大差距;Rudy 和Webb 考虑了肋片侧壁面表面张力对凝液迁移的作用及淹没区对换热的影响，建立了换热系数计算式［5］，与试验研究的R134a 与R12 在低肋管上冷凝换热系数的比较［6］，该模型预测值偏低表明其适用范围受到肋管表面结构的限制;Honda针对梯形肋管，考虑了淹没区和非淹没区的换热特性及表面张力导致的液膜压力梯度在圆周上的变化，建立了换热系数计算式［7］，并与Kumar 以水蒸气和R134a 为工质，对7 种不同肋片管进行试验所得到的凝结换热系数比较［8］，Honda 计算式对水蒸汽换热系数比试验值偏低，而对R134a 换热系数偏高，使其在工程领域中的应用受到限制;对不同制冷工质在肋片管外的冷凝换热、肋片高与肋间距的优化进行了大量试验［9～11］，但理论研究尚存在不足。

目前，纯饱和工质在二维表面膜状凝结换热理论仍不完善，因此，本文对R134a 在梯形肋片管外的凝结换热进行研究，考虑其他模型所忽略的肋间基管处表面张力导致的液膜压力梯度沿周向分布的影响，建立肋片侧壁和肋间基管处液膜分布模型，最后得到管外平均凝结换热系数。

1 建立物理模型

如图1所示，在肋片侧壁上，取任意的微元凝液，设X 为沿管壁切向方向，Y 为沿肋片高度垂直基管方向，Z 为垂直肋片侧壁方向;x 为基管上从肋间中点到肋根的方向，在x =0 处，液膜厚度为δb，如图1(c)所示。

物理模型采用极坐标形式，肋侧壁任意微元凝液的位置(r，θ)处的方程为

对任意微元角度dθ 内，凝结在肋侧壁上微小面积为rdθdr。

在肋间基管处任意微元凝液的位置为(θ，x)，基管上的微小面积为rbdθdx。

图1 凝结液膜物理模型Fig.1 Physical model of condensate film

2 控制方程及边界条件

为便于计算，做如下假设:(1)常物性，液体为不可压缩牛顿流体;(2)纯蒸汽是静止的所以对凝结液膜表面无剪切应力;(3)液膜惯性力可以忽略不计;(4)沿径向液膜主要受表面张力作用可以忽略重力作用;(5)沿圆周方向对液膜流动起主要作用的是重力，所以忽略表面张力作用;(6)液膜内温度分布是线性的，即液膜内热量转移只有导热，无对流作用;(7)汽液界面上无温差，液膜表面温度等于饱和温度，即tδ=ts;(8)液膜表面平整无波动;(9)液膜内的过冷度可以忽略不计;(10)冷凝管壁温不随管长变化。

由此得肋片侧壁上液膜的动量守恒方程［12］为

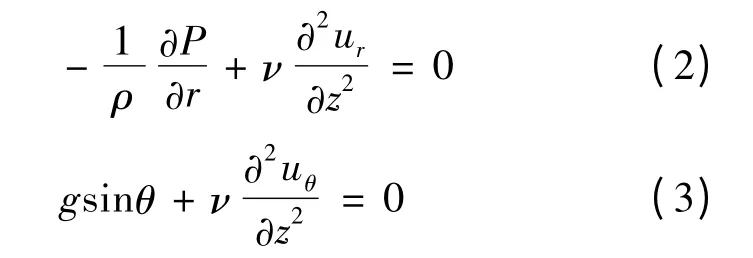
边界条件:在肋片侧壁面上，即Z=0

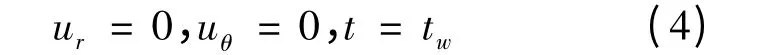
在肋片侧壁汽液界面上，即Z=δfik

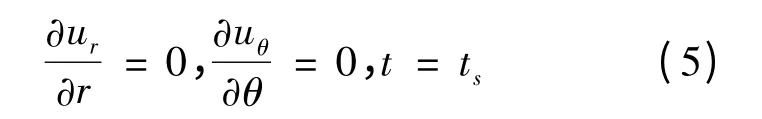
由式(2)～(5)得液膜在肋片侧壁径向和周向的流动速度为

图1(c)肋间基管的凝结液膜厚度计算式［13］为

边界条件:

式(8)左侧第1 项表示重力引起的压力梯度使凝液沿周向流动的凝结液率;第2 项表示因表面张力引起的压力梯度使凝液沿x 方向流动的凝结液率;右侧表示冷凝率。由式(8)、(9)整理得:

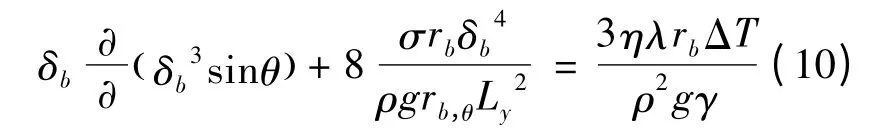
径向方向的压力梯度［14］为

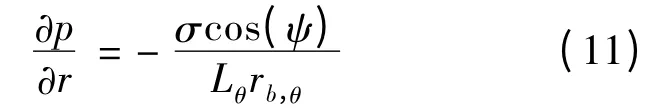
由式(6)、(7)得肋片侧壁上液膜流动速度为

凝结液在肋根处液膜曲率半径［13］为

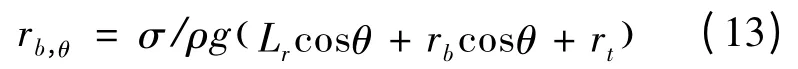
式(12)中肋侧壁有效换热高度Lθ，由图1(c)可得:

如图2所示，设微元肋片侧壁上B 处凝结液膜的切线与肋壁面平行，所以∠ABC 等于Ψ。肋

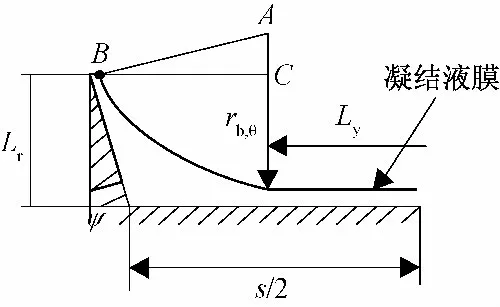
图2 肋根与基管相连处液膜分布Fig.2 Film distribution on fin root and base tube

片间液膜厚度为δb处的宽度Ly为

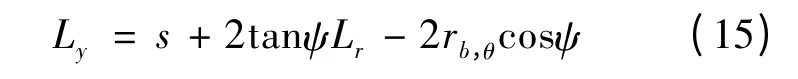
3 液膜厚度的确定

由式(12)可得，在肋片侧壁微元肋高dr 内液膜质量流量qm，即

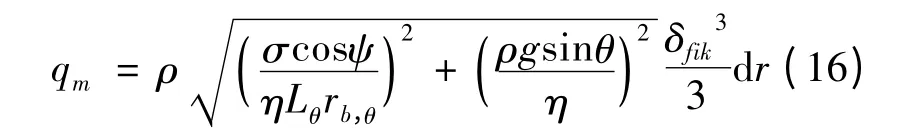
如图3所示，面1234 为肋片的侧壁面，面5678 为汽液界面。在θ +dθ 处，微元肋高dr 内液膜增加dδfik时的质量流量增加量dqm为

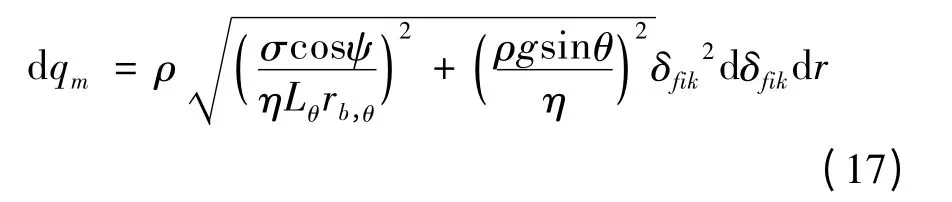
图3 肋片侧壁凝结液微元体质量流量Fig.3 Mass flow of condensate film on element fin flank

根据假定(6)蒸汽凝结放出的潜热等于液膜导给壁面的热量，得到热平衡方程:

肋片侧壁上非淹没区液膜的厚度分布式:

整理肋间基管上液膜厚度分布式(10)得:

4 凝结换热系数的确定

由式(19)、(20)确定的液膜厚度分别得肋片侧壁面及基管处微元凝结换热系数为

式中:δ 表示液膜厚度;h′表示局部凝换热系数。当已知肋片侧壁上凝结液膜厚度δfik和肋间基管处凝结液膜厚度δb时，可得肋片侧壁处微元凝结换热系数h′fik和肋片基管处微元凝结换热系数h′b。由于淹没区凝结液完全淹没肋片及基管，热阻很大忽略淹没区换热。

水平肋片管平均凝结换热系数为

式中:Sfik为肋片侧壁有效换热面积，m2;Sb为基管有效换热面积，m2;Δt 为凝结汽饱和温度与壁面温差，℃;Qfik为单位管长上肋壁面换热量;Qb为单位管长上基管换热量。

5 滞留角的确定

水平翅片管外凝结换热，凝结液膜受重力、粘滞力、表面张力的共同作用，在管子的底部会有凝结液的滞留现象，在冷凝管上冷凝液滞留的范围用滞留角表示。肋片管换热的有效区为非淹没区，即图1(a)中圆周角0°～φf范围。非淹没区角度的计算式［14］为

6 实例计算及分析

文献［15］测试纯饱和R134a 蒸汽自然对流时在3 种不同管外的平均冷凝换热系数，并给出了详细的试验程序和数据评估，选取文献［15］中的肋片管计算，基管外径为16.85 mm，肋片高度为0.95 mm，肋片间距为0.64 mm 标准肋片管，管外纯制冷剂(R134a)饱和蒸汽温度为37 ℃，以饱和温度与管壁温度的平均值作为凝结液膜的物性温度，设沿管壁及肋片上的冷凝温度保持不变。计算结果与文献［15］中实验结果比较，如图4。模型计算结果与实验数据变化趋势一致，且平均绝对误差最大值为7.6 %。

选取肋高为1.45 mm，基管直径为16 mm，且肋片密度为11 fins/inch 的K11 和管径和肋高同K11 管相同但肋片间距不同的K19 管(肋片密度为19 fins/inch)管进行计算比较。不同壁面温度时，基管处的凝结液膜分布以及换热系数变化如图5，6所示。

图4 与实验数据对比的换热系数Fig.4 Heat transfer coefficient compared with experimental data

图5 基管液膜厚度Fig.5 Film thickness on base tube

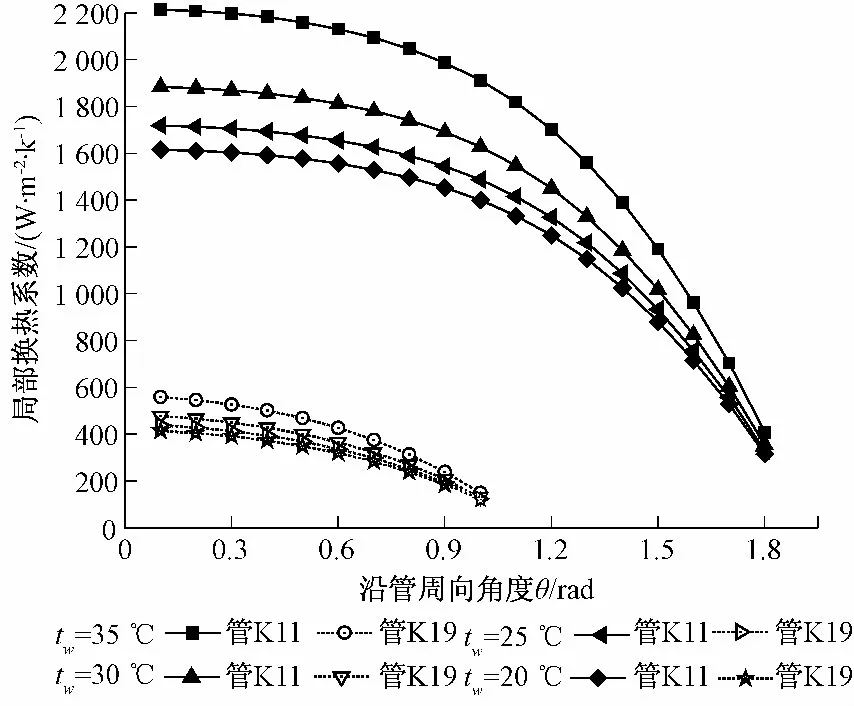
图6 基管上局部凝结换热系数Fig.6 Local heat transfer coefficient on base tube

基管上沿θ 角增大方向液膜分布逐渐增厚，接近凝结液滞留角时，液膜厚度急剧增加，K11 管比K19 管的液膜薄(图5)，这是因为肋间距小，凝结液与两肋片表面间的粘滞力较大而不易排出，使液膜变厚;局部凝结换热系数沿θ 角增大方向逐渐减小，接近凝结液滞留角时，急剧减小(图6)，主要原因为:凝结液膜厚度增大，使热阻增加，总的传热系数越小;K11 管凝结液非滞留角大于K19 管，是由于K11 的肋片间距大于K19 的肋片间距，肋间距小的管子更容易发生凝结液的滞留;在重力和液膜粘滞力的作用，基管管顶(θ=0°处)液膜最薄，热阻也最小，凝结换热系数最大;液膜厚度沿θ 角增大方向逐渐增加，故换热热阻也随之增加，换热系数减小。

K19 管的肋片侧壁处的凝结液膜厚度分布和局部凝结换热系数分布，如图7，8所示。在0° ＜θ＜π/2 范围内，肋片侧壁上沿肋径向方向液膜厚度逐渐减小，沿θ 角增大方向液膜不断增厚(图7)，因液膜受表面张力作用产生的压力梯度使凝液由肋顶向肋根聚集，所以沿肋径向方向液膜逐渐变薄，液膜因表面张力作用受到的纵向方向力与重力同向，加速肋侧壁凝结液的迁移，故沿θ 角增大方向液膜不断增厚;肋片侧壁上局部凝结换热系数沿径向方向增大，沿θ 角增大方向减小(图8)，因凝结液膜是换热主要热阻，所以换热系数随液膜的增厚而减小。

图7 肋侧壁液膜厚度沿肋高及圆周角方向分布Fig.7 Film thickness on fin flank with the change of the fin height and circular angle

如图9所示，在相同单位管长换热量，K11 管凝结换热系数高于K19 管。因K11 管单位长度上换热面积小于K19 管;肋间距小，使相邻肋片间易形成凝结液滞留的区域，阻碍凝结液的排出，增加了换热热阻及凝结液滞留角，造成有效换热面积减小，导致换热性能下降。因此，适当的肋片间距能够达到最佳的换热效果，通过肋间距优化，选择合理的肋片布置方案，使冷凝器的效率提高。

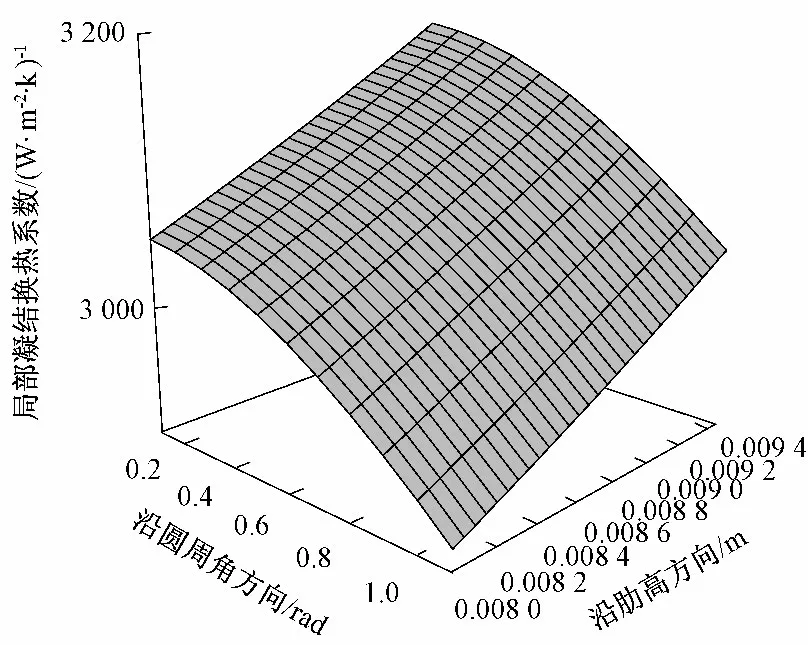
图8 肋片侧壁凝结换热系数沿肋高及圆周角方向分布Fig.8 Heat transfer coefficient on fin flank with the change of the fin height and circular angle

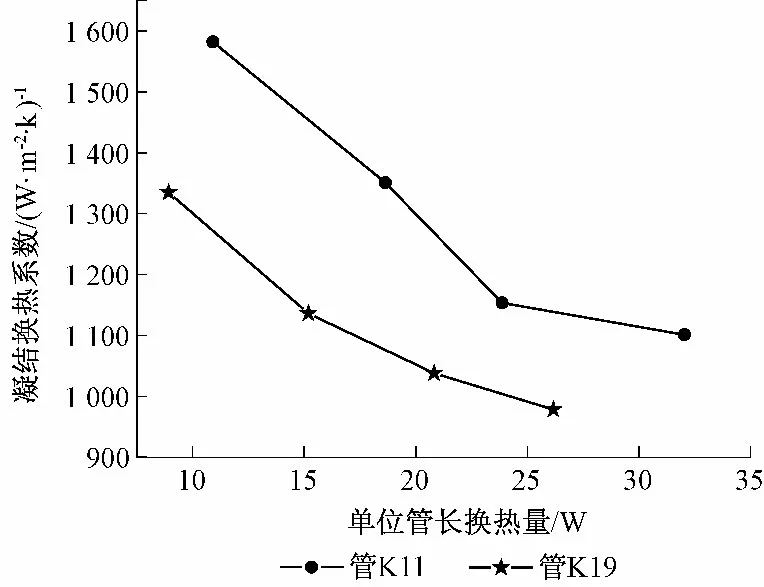
图9 不同肋片间距管换热性能比较Fig.9 Heat transfer performance comparison of fin-tubes with different fin pitch

7 结论

(1)本文通过建立水平肋片管的物理模型，推导出液膜厚度及换热系数计算式，通过与实验值比较，验证了所建模型的正确性，同时分别对肋片侧壁和肋间基管液膜厚度及换热系数进行了计算;

(2)肋片管肋片侧壁上凝结液膜沿θ 角增大方向增厚，沿肋径向方向不断减薄，换热系数沿θ角增大方向不断减小，沿肋径向方向不断增加;

(3)肋间基管上凝结液膜厚度沿θ 角增大方向逐渐增厚，凝结换热系数逐渐减小;

(4)在其它条件相同时，肋片的间距大小对换热性能有较大的影响，适当的肋片管间距，可提高换热性能。

因此，通过本文所建的液膜厚度分布及换热系数模型，可以优化肋片间距，为强化凝结换热性能提供一定的参考。

符号说明:

ρ 为密度，kg/m3;g 为重力加速度，m/s2;λ 为导热系数，W/(m.K);v 为运动粘度，m2/s;η 为动力粘度，Pa.s;γ 为汽化潜热，kJ/kg;h 为换热系数，W/(m2.K);Q 为单位管长换热量，W;σ 为表面张力;qm为凝结液质量流量kg/(m2.s);δ 为液膜厚度m;p 为压力，pa;r 为半径，m;rb，θ为液膜曲率半径，m;θ 为圆周角，rad;Ψ 为肋顶角一半，rad;Φf为非淹没角，rad;z 为Z 方向的坐标值;ur为径向速度，m/s;uθ为周向速度，m/s;S 为面积，m3;Ll为肋片高度，m;Lθ为有效换热肋高，m;Lr为基管处凝液高度，m;Ly为基管液膜无曲率长度，m;d 为直径，m。下标，b 为基管;t 为肋顶;fik 为肋侧壁。上标，ˊ为微元处;‐为平均值。

［1］沈雅钧，崔肖洁，杨永华.翅片管强化传热技术在冷凝器中的应用［J］.浙江海洋学院学报(自然科学版)，2009，4:480－485.

［2］Beatty K O，Katz.D L.Condensation of vapours on outside of finned tube［J］.Chemical Engineering Progress.1948，44 (1):55－77.

［3］Cheng W Y，Wang C C.Condensation of R134a on enhanced tubes［J］.ASHRAE Transaaction，1994，100(2):809－817.

［4］Karkhu V A，Borovkov V P.Film condensation of vapour at finely-finned horizontal tubes［J］.Heat Transfer Soviet Research.1971，3;183－191.

［5］Webb R L，Rudy T M，Keswan S T.Prediction of the condensation coefficient on horizontal integral fin tube［J］.Journal of Heat Transfer，1985，107:369－376.

［6］张定才，刘启斌，陶文铨等.R22 在水平双侧强化管外的凝结换热［J］.化工学报.2005，56 (10):1865－1868.

［7］Honda H，Nozu S.A prediction method for heat transfer during film condensation on horizontal low integral-fin tubes［J］.Journal of Heat Transfer.1987，109:218－225.

［8］Kumar R，Varma H K，A Comprehensive Study of Modified Wilson Plot Technique to Determine the Heat Transfer Coefficient during Condensation of Steam and R－134a over Single Horizontal Plain and Finned Tubes［J］.Heat Transfer Engineering.2001，Vol.2，NO.2，3－12.

［9］贾传林，欧阳新萍，陈建红等.R22 和R417A 在水平强化管外的凝结换热实验研究［J］.制冷学报，2009，30 (4):31－35.

［10］洪思雯，欧阳新萍，贾传林等.一种冷凝强化换热管传热性能的试验研究［J］.制冷学报，2009，30(1)，30－34.

［11］黄志光，汪荣顺，石玉美等.水平管外二氧化碳膜状凝结传热分析［J］.制冷学报，2005，26 (4):6－11.

［12］黄庆达.N-S 方程在不同坐标中的直接导出［J］.天津理工学院学报.2000，16 (4):20－24.

［13］J.W.Rose.An analysis of film condensation on a horizontal wire-wrapped tube［J］.Institution of Chemical Engineers Trans IChemE，.Vol 80，Part A，ril 2002.

［14］Honda H，Nozu S，Mtsumori K.Augmentation of condensation on horizontal tubes by attachinging a porous drainage plate［C］//Proc ASME-JSME Thermal Engineering Joint Conference.Hawaii: ASME，1983(3):289－296.

［15］T.Gebauer，A.R.Al-badri，A.gotterbarm，et al.Condensation heat transfer on single horizontal smooth and finned tubes and tube bundles for R134a and propane，Int.J.Heat Mass Transfer 56 (2013)516－524.